算法设计与分析实验报告-分治法相关练习题

课本分治法章节课后部分练习题。

算法设计与分析实验报告-递归与分治策略

算法设计与分析实验报告-动态规划算法

算法设计与分析实验报告-回溯法

算法设计与分析实验报告-分治法相关练题

北京大学出版社-算法设计与分析

五、程序题

1. 试给出用分治法求某集合中元素值为偶数的元素个数的程序代码。

2. 试给出用i分治法求某集合中元素值为最大数的程序代码。

3. 根据分治法求某集合中元素值大于指定值的元素个数。要求给出分治法解决该问题的基本思路并给出递归实现代码。

4. 根据分治法求解棋盘覆盖问题。试写出该程序代码，可以只写函数

5. 给出归并排序的核心代码，并分析归并排序的时间复杂性。

6. 给出快速排序算法，以及快速排序的Partition函数。

7. 给出分治法设计的循环赛日程表。

8. 用分治法写出有序序列进行二分查找的过程

9. 对给定的含有n个元素的无序序列，求这个元素中第K小的元素

分治法求某集合中元素值大于指定值的元素个数。基本思路：将求解范围l~r分为两半，变成2个子问题，递归求解两个子问题，再将两个子问题的解加和得到原问题解。 
递归出口：只有一个元素时与指定元素进行比较返回答案1或0. 
递归关系：两个子问题的解相加为原问题解。 
参数设置：数组arr，起始位置l，终点位置r，指定比较值x。

1. 试给出用分治法求某集合中元素值为偶数的元素个数的程序代码。

//
// Created by GiperHsiue on 2022/10/17.
//
// 分治法求某集合中元素值为偶数的元素个数。
#include <iostream>
using namespace std;
int check(int arr[], int l, int r){if(l == r) return arr[l] % 2 ? 0 : 1;int mid = l + r >> 1;return check(arr, l, mid) + check(arr, mid + 1, r);
}
int main(){int n;cin >> n;int *arr = new int[n];for(int i = 0; i < n; i ++) cin >> arr[i];cout << check(arr, 0, n - 1);return 0;
}

运行如下：

2. 试给出用分治法求某集合中元素值为最大数的程序代码。

//
// Created by GiperHsiue on 2022/10/17.
//
//分治法求某集合中元素值为最大数。
#include <iostream>
#include <algorithm>
using namespace std;
int check(int arr[], int l, int r){if(l == r) return arr[l];int mid = l + r >> 1;return max(check(arr, l, mid), check(arr, mid + 1, r));
}
int main(){int n;cin >> n;int *arr = new int[n];for(int i = 0; i < n; i ++) cin >> arr[i];cout << check(arr, 0, n - 1);return 0;
}

测试如下：

3. 根据分治法求某集合中元素值大于指定值的元素个数。要求给出分治法解决该问题的基本思路并给出递归实现代码。

//
// Created by GiperHsiue on 2022/10/17.
//
#include <iostream>
#include <algorithm>
using namespace std;
int check(int arr[], int l, int r, int x){if(l == r) return arr[l] > x ? 1 : 0;int mid = l + r >> 1;return check(arr, l, mid, x) + check(arr, mid + 1, r, x);
}
int main(){int n, x;cin >> n;int *arr = new int[n];for(int i = 0; i < n; i ++) cin >> arr[i];cin >> x;cout << check(arr, 0, n - 1, x);return 0;
}

测试如下：

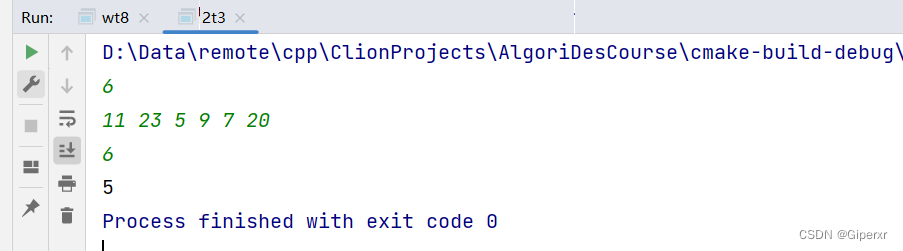
4. 根据分治法求解棋盘覆盖问题。试写出该程序代码，可以只写函数。

//
// Created by GiperHsiue on 2022/10/20.
//
//棋盘覆盖问题
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
char tile = '1'; // 骨牌的编号
char **board;
//(r,c)棋盘左上角坐标，(sr,sc)特殊方格坐标，size棋盘的行（列）数
void cb(int r, int c, int sr, int sc, int size){if(size == 1) return;int t = tile++;int s = size / 2;//左上角if(sr < r + s && sc < c + s){cb(r, c, sr, sc, s);} else{board[r + s -1][c + s - 1] = t;cb(r, c, r + s - 1, c + s - 1, s);}//右上角if(sr < r + s && sc >= c + s){cb(r, c + s, sr, sc, s);} else{board[r + s -1][c + s] = t;cb(r, c + s, r + s - 1, c + s, s);}//左下角if(sr >= r + s && sc < c + s){cb(r + s, c, sr, sc, s);} else{board[r + s][c + s - 1] = t;cb(r + s, c, r + s, c + s - 1, s);}//右下角if(sr >= r + s && sc >= c + s){cb(r + s, c + s, sr, sc, s);} else{board[r + s][c + s] = t;cb(r + s, c + s, r + s, c + s, s);}
}
int main(){int k;cout << "棋盘大小2^k * 2^k 输入K:";cin >> k;int n = pow(2, k);board = new char*[n]; //动态创建棋盘数组for(int i = 0; i < n; i ++) board[i] = new char[n];for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {board[i][j] = '.';}}cout << "输入特殊方格位置：";int sr, sc;cin >> sr >> sc;board[sr][sc] = '*';cout << "初始化：" << endl;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {cout << setw(4) << board[i][j];}cout << endl;}cb(0, 0, sr, sc, n);cout << "覆盖后：" << endl;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if(i == sr && j == sc) cout << setw(4) << board[i][j];else cout << setw(4) << board[i][j] - '0';}cout << endl;}return 0;
}

测试如下：

5. 给出归并排序的核心代码，并分析归并排序的时间复杂性。

//
// Created by GiperHsiue on 2022/10/20.
//
//归并排序
#include <iostream>
using namespace std;
int n;void mergeSort(int a[], int l, int r){if(l >= r) return;int mid = (l + r) / 2;mergeSort(a, l, mid), mergeSort(a, mid + 1, r);//merge过程int k = 0, i = l, j = mid + 1;int *tmp = new int[n]();while (i <= mid && j <= r) {if (a[i] <= a[j]) tmp[k++] = a[i++];else tmp[k++] = a[j++];}while(i <= mid) tmp[k++] = a[i++];while (j <= r) tmp[k++] = a[j++];//copy过程for (i = l, j = 0;i <= r; i++, j++) {a[i] = tmp[j];}
}
int main(){cin >> n;int *a = new int[n]();for (int i = 0; i < n; ++i) {cin >> a[i];}mergeSort(a, 0, n - 1);for (int i = 0; i < n; ++i) {cout << a[i] << ' ';}return 0;
}

时间复杂度分析：T(n)=2T(n/2)+n

通过主方法可得T(n)=O(n*logn)

主方法公式（Master）：

测试如下：

6. 给出快速排序算法，以及快速排序的Partition函数。

//
// Created by GiperHsiue on 2022/10/20.
//
//快速排序
#include <iostream>
using namespace std;
int Partition(int a[], int l, int r){int x = a[l], i = l - 1, j = r + 1;while (i < j){do i++; while (a[i] < x);do j--; while (a[j] > x);if (i < j) swap(a[i], a[j]);}return j;
}
void quickSort(int a[], int l, int r){if (l >= r) return;int q = Partition(a, l, r);quickSort(a, l, q), quickSort(a, q + 1, r);
}int main(){int n;cin >> n;int *a = new int[n];for (int i = 0; i < n; ++i) {cin >> a[i];}quickSort(a, 0, n - 1);for (int i = 0; i < n; ++i) {cout << a[i] << ' ';}return 0;
}

测试如下：

7. 给出分治法设计的循环赛日程表。

//
// Created by GiperHsiue on 2022/10/20.
//
// 循环赛日程表
#include<iostream>
#include<cmath>
using namespace std;void schedule(int k, int n, int** array);int main()
{int k;  // 运动员的人数n=2^kcout << "运动员的人数为n（n=2^k），请输入k的值：";cin >> k;int n = pow(2, k);  // 运动员的人数n=2^kint** array = new int* [n+1]; // 循环赛日程表，动态数组的创建for (int i = 0;i < n+1;i++)array[i] = new int[n+1];// 填充日程表schedule(k, n, array);// 输出日程表cout << "\n循环赛日程表为：\n";for (int i = 1;i <= n;i++){for (int j = 1;j <= n;j++)cout << array[i][j] << " ";cout << "\n";}// 删除二维数组for (int i = 0;i < n + 1;i++)delete[] array[i];delete[] array;return 0;
}void schedule(int k, int n, int** array)   // 数组下标从1开始
{for (int i = 1;i <= n;i++)  // 第一行排1-narray[1][i] = i;int m = 1;  // 用来控制每一次填表时i行j列的起始填充位置for (int s = 1;s <= k;s++)  // k指分成k大部分进行填充日程表；s指第几大部分{n = n / 2;for (int t = 1;t <= n;t++)  // 第s部分内的循环{for (int i = m + 1;i <= 2 * m;i++) // 行{for (int j = m + 1;j <= 2 * m;j++) // 列{array[i][j + (t - 1) * m * 2] = array[i - m][j + (t - 1) * m * 2 - m];       //左上角等于右下角的值array[i][j + (t - 1) * m * 2 - m] = array[i - m][j + (t - 1) * m * 2];       //左下角等于右上角的值}}}m *= 2;}
}

测试如下：

8. 用分治法写出有序序列进行二分查找的过程。

//
// Created by GiperHsiue on 2022/10/20.
//
//二分查找，给出过程
#include <iostream>
using namespace std;
int t = 1;
int BinSearch(int a[], int l, int r, int k){int mid = 0;if(l <= r){mid = (l + r) / 2;cout << "第" << t++ << "次比较:" << " mid = " << mid << " a[mid] = " << a[mid] << endl;if (a[mid] == k) return mid;else if (a[mid] < k) return BinSearch(a, mid + 1, r, k);else return BinSearch(a, l, mid - 1, k);}return -1;
}
int main(){int a[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, k;for(auto x:a) cout << x << ' ';cout << endl;cin >> k;int res = BinSearch(a, 0, 9, k);cout << "查找结果位置下标：" << res;return 0;
}

测试如下：

9. 对给定的含有n个元素的无序序列，求这个元素中第K小的元素。

法1，可以利用快排思想，在快速排序基础上，在每次划分以后，判定所找元素在哪一边，再只对所在一半继续递归进行划分，直到找到确定位置返回。

法2如下；

//
// Created by GiperHsiue on 2022/10/20.
//
// 对给定的含有n个元素的无序序列，求这个序列中第k小的元素。
// 
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int select(int a[], int start, int end, int k) {int n = end - start;if (n < 5) {sort(a + start, a + end);return a[start + k - 1];}int s = n / 5;int *m = new int[s];   //中位数数组int i;for (i = 0; i < s; i++) {sort(a + start + i * 5, a + start + i * 5 + 5);m[i] = a[start + i * 5 + 2];}sort(m, m + i);int mid = m[i / 2];int *a1 = new int[n];int *a2 = new int[n];int *a3 = new int[n];int num1 = 0, num2 = 0, num3 = 0;for (int i = start; i < end; i++) {if (a[i] < mid)a1[num1++] = a[i];else if (a[i] == mid)a2[num2++] = a[i];elsea3[num3++] = a[i];}if (num1 >= k)return select(a1, 0, num1, k);if (num1 + num2 >= k)return mid;elsereturn select(a3, 0, num3, k - num1 - num2);
}int main() {int n;cout << "输入个数n：";cin >> n;int *a = new int[n];cout << "输入数组元素：";for (int i = 0; i < n; i++)cin >> a[i];int k;cout << "输入所求第几小元素k：";cin >> k;cout << "第" << k << "小元素为：" << select(a, 0, n, k) << endl;delete[] a;return 0;
}

测试如下：