数据结构之BinaryTree（二叉树）的实现

BinaryTree要实现的方法

总结

  1. remove不在BinNode里，而是BinTree里

  2. 递归的两种写法
    从上往下：同一对象的递归（参数多一个，判空用一句话），子对象的递归（参数void，判空用两句话）（因为分叉，所以递归是真递归）
    从下往上：不分叉，为了效率，可以用循环

// 我的最初写法（递归更新一条路径上的全部节点high值）
template <typename T>
void BinNode<T>::updateHigh(void)
{int oldHigh = high;high = std::max(getHigh(left), getHigh(right)) + 1;if (parent != NULL && oldHigh != high) parent->updateHigh();
}// 调用
rt->updateHigh();

// 改良版（循环更新一条路径上的全部节点high值）
template <typename T>
void BinTree<T>::updateHighAbove(BinNode<T> * rt)
{while (rt){if (!rt->updateHigh()) break; //这是书里说的优化，但书中并未实现rt = rt->parent;}
}
template <typename T>
bool BinNode<T>::updateHigh(void) //返回是否更新了树高
{int oldHigh = high;high = std::max(getHigh(left), getHigh(right)) + 1;return oldHigh != high;
}
// 调用
updateHighAbove(rt);

  1. 整棵树与根节点的区别：整棵树的类型是BinTree 而根节点的类型是BinNode。二者都有成员变量high和size改了根节点的size，没改整棵树的size

  2. 发现high也有上一条的问题。书上BinTree没有设置high，BinNode没有size，那就删掉，省的单独更新

  3. 为什么remove写两个，因为切断来自parent的指针和更新高度不用层层进行，还是为了提高效率。remove_core负责递归，remove在最外层负责切断来自parent的指针和更新高度

  4. remove如果rt是根节点那么不进行切断来自parent的指针和更新高度，析构函数要用

  5. 静态成员函数可以不依附于具体对象来调用。为了调用时简洁。静态成员函数就很像是面向过程了

code BinNode

# pragma once
# include <algorithm>
# define getHigh(x) x ? x->high : -1// 仿函数：打印功能
template <typename T>
struct print {void operator ()(T data){std::cout << data << std::endl;}
};template <typename T>
struct BinNode {int high;T data;BinNode<T> * left;BinNode<T> * right;BinNode<T> * parent;int Size(BinNode<T> * x){if (x){return 1 + Size(x->left) + Size(x->right);}return 0;}BinNode(T const & d, BinNode<T> * p) : data(d), parent(p), left(NULL), right(NULL), size(1), high(0) {}BinNode<T> * insertAsLeft(T const & val){left = new BinNode<T>(val, this);return left;}BinNode<T> * insertAsRight(T const & val){right = new BinNode<T>(val, this);return right;}bool updateHigh(void){int oldHigh = high;high = std::max(getHigh(left), getHigh(right)) + 1;return oldHigh != high;}template <typename T2>void travPre(T2 visit){visit(data);if (left) left->travPre(visit);if (right) right->travPre(visit);}template <typename T2>void travIn(T2 visit){if (left) left->travIn(visit);visit(data);if (right) right->travIn(visit);}template <typename T2>void travPost(T2 visit){if (left) left->travPost(visit);if (right) right->travPost(visit);visit(data);}
};

code BinTree

# pragma once
# include "BinNode.h"template <typename T>
class BinTree
{
protected:
public:int size;BinNode<T> * root;public:BinTree():size(0), root(NULL){}~BinTree() { if (root) remove(root); }//***********************************************************只读*********************************************************int Size(void) const { return size; }bool empty(void) const { return size == 0; }BinNode<T> * Root(void) const { return root; }//***********************************************************可写*********************************************************// 节点插入BinNode<T> * insertAsRoot(T const & e){size = 1;root = new BinNode<T>(e, NULL);return root;}BinNode<T> * insertAsLeft(T const & e, BinNode<T> * rt){++size;rt->insertAsLeft(e);updateHighAbove(rt);return rt->left;}BinNode<T> * insertAsRight(T const & e, BinNode<T> * rt){++size;rt->insertAsRight(e);updateHighAbove(rt);return rt->right;}// 子树接入,返回接入位置rtBinNode<T> * attachAsLeft(BinTree<T> * newSubtree, BinNode<T> * rt){size += newSubtree->size;rt->left = newSubtree->root;updateHighAbove(rt);// 清空newSubtree原来的东西newSubtree->size = 0;newSubtree->root = NULL;return rt;}BinNode<T> * attachAsRight(BinNode<T> * newSubtree, BinNode<T> * rt){size += newSubtree->size;rt->right = newSubtree->root;updateHighAbove(rt);// 清空newSubtree原来的东西newSubtree->size = 0;newSubtree->root = NULL;return rt;}int remove(BinNode<T> * rt){// 切断来自parent的指针fromParentTo(rt) = NULL;// 更新高度updateHighAbove(rt->parent);int ans = remove_core(BinNode<T> * rt);size -= ansreturn ans;}int remove_core(BinNode<T> * rt){if (!rt) return 0; // 递归出口int ans = remove(rt->left) + remove(rt->right) + 1;delete rt;return ans;}BinTree<T> * secede(BinNode<T> * rt) // 先不考虑 如果rt是树根{// 切断来自parent的指针fromParentTo(rt) = NULL;size -= BinNode<T>::Size(rt);BinTree<T> * newTree = new BinTree<T>();newTree->root = rt;rt->parent = NULL;updateHighAbove(rt->parent);return newTree;}void updateHighAbove(BinNode<T> * rt){while (rt){if (!rt->updateHigh()) break;rt = rt->parent;}}//***********************************************************遍历*********************************************************template <typename T2>void travPre(T2 visit){if (root) root->travPre(visit);}template <typename T2>void travIn(T2 visit){if (root) root->travIn(visit);}template <typename T2>void travPost(T2 visit){if (root) root->travPost(visit);}private:BinNode<T> * & fromParentTo(BinNode<T> * x){if (x == x->parent->left) return x->parent->left;else return x->parent->right;}
};

测试程序（树的结构如图）

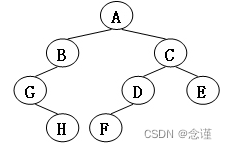
在这里插入图片描述

# include <iostream>
# include "BinTree.h"int main(void)
{BinTree<char> T1;BinNode<char> * pA = T1.insertAsRoot('A');BinNode<char> * pB = T1.insertAsLeft('B', pA);BinNode<char> * pG = T1.insertAsLeft('G', pB);BinNode<char> * pC = T1.insertAsRight('C', pA);BinNode<char> * pE = T1.insertAsRight('E', pC);BinNode<char> * pH = T1.insertAsRight('H', pG);BinNode<char> * pD = T1.insertAsLeft('D', pC);BinNode<char> * pF = T1.insertAsLeft('F', pD);print<int> p;std::cout << T1.Size() << '\n';// 高度测试std::cout << "根高度：";  std::cout << T1.Root()->high; std::cout << "\n";std::cout << "C高度：";  std::cout << pC->high; std::cout << "\n";// 遍历测试std::cout << "后序遍历："; T1.travPost(p); std::cout << "\n";std::cout << "中序遍历："; T1.travIn(p); std::cout << "\n";// 移除测试std::cout << "删掉：" << T1.remove(pD) << "个节点" << '\n';std::cout << "C高度：";  std::cout << pC->high; std::cout << "\n";std::cout << "中序遍历："; T1.travIn(p); std::cout << "\n";std::cout << T1.Size() << '\n';// 切断测试BinTree<char> * pT2 = T1.secede(pC);std::cout << "中序遍历T1："; T1.travIn(p); std::cout << "\n";std::cout << "中序遍历T2："; pT2->travIn(p); std::cout << "\n";std::cout << T1.Size() << '\n';std::cout << pT2->Size() << '\n';return 0;
}

输出

8
根高度：3
C高度：2
后序遍历：H G B F D E C A
中序遍历：G H B A F D C E
删掉：2个节点
C高度：1
中序遍历：G H B A C E
6
中序遍历T1：G H B A
中序遍历T2：C E
4
2

迭代遍历

上面的代码是递归的遍历。现在再写迭代的前序、中序、后序遍历。

尾递归

前序遍历的递归代码，左右子树都属于尾递归。中序遍历的递归代码，右子树属于尾递归。而后序遍历完全不属于尾递归。所以后序遍历比前、中序遍历复杂得多。要理解这句话，还要先了解尾递归转成迭代的方法，而这也是编译器在编译之前常做的优化手段。

以汉诺塔为例，理解递归转迭代

BinTree 的三个遍历接口不变，只需修改BinNode 的遍历函数。

travPre迭代1：直接转化（但不可推广到中、后序）

仅说思路：根节点进栈。当栈非空：出栈访问，然后右子树入栈，左子树入栈。

这个完全模拟了尾递归时编译器的操作。至于为什么先右后左，因为这样出栈时才能先左后右。

（汉诺塔那篇文章如果你把结果打印出来，发现迭代的结果跟递归结果是反过来的，如果将入栈的两句话交换位置，那么输出结果一模一样）

travPre迭代2：新思路（可推广）

我们通过仔细观察travPre，得到前序遍历的迭代算法。

	template <typename T2>void travPre(T2 visit){// 出栈，访问visit(data);// 左侧链一路访问到底if (left) left->travPre(visit);// 每访问一个左孩子，将对应右孩子进栈备用if (right) right->travPre(visit);}

迭代2的算法

	template <typename T2>void travPre2(T2 visit){// 出栈顶。右孩子进栈，访问左孩子。转到左孩子，重复上一步。直到没有左孩子，出栈顶。BinNode<T> * current;Stack<BinNode<T>*> s;s.push(this);while (!s.empty()){current = s.pop();		while (current){visit(current->data);if (current->right) s.push(current->right);current = current->left;}}}

travIn迭代

按图索骥，继续先观察递归算法

	void travIn(T2 visit){// 沿左侧链一路向左进栈if (left) left->travIn(visit);// 没有左子树时，出栈访问visit(data);// 访问完马上转到右儿子，进一个栈if (right) right->travIn(visit);}

travIn迭代算法

	template <typename T2>void travIn2(T2 visit){// 左孩子进栈，没有左孩子时，出栈顶访问，一个右孩子进栈，右孩子的左孩子到底进栈BinNode<T> * current = this;Stack<BinNode<T>*> s;while (current){s.push(current);current = current->left;}while (!s.empty()){current = s.pop();visit(current->data);current = current->right;while (current){s.push(current);current = current->left;}}}

travPost迭代

比较复杂。邓老师将其描述为，藤绕树。先找藤的头。

善后工作

为了调用更加友好，BinTree 的三个遍历接口加一个tag参数，缺省为0，宏定义ITER(意为迭代)为1

	template <typename T2>void travPre(T2 visit, int tag = 0){if (root){if (tag & ITER) root->travPre2(visit);else root->travPre(visit);}}template <typename T2>void travIn(T2 visit, int tag = 0){if (root){if (tag & ITER) root->travIn2(visit);else root->travIn(visit);}}template <typename T2>void travPost(T2 visit, int tag = 0){if (root){if (tag & ITER) root->travPost2(visit);else root->travPost(visit);}}

theeeend ₍ᐢ…ᐢ₎♡

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/5739.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

python数据分析05—Pandas数据处理

python数据分析05—Pandas数据处理

目录 1.缺失数据处理 1.1 DataFrame自身产生的缺失数据 1.2 缺失数据判断和统计 ​1.3 缺失数据清理 2. 多源数据操作 2.1 合并函数&#xff1a;merge() 2.2 连接函数&#xff1a;join() 2.3 指定方向合并&#xff1a;concat() 3. 数据分组和聚合运算 3.1 groupby()方…
阅读更多...
（34）继电器开关

（34）继电器开关

文章目录 前言 34.1 装有IOMCU的自动驾驶仪上的继电器引脚 34.2 通过任务规划器定义继电器引脚 34.3 飞行员控制继电器 34.4 任务控制继电器 34.5 任务规划器控制继电器 前言 "继电器"是自动驾驶仪上的一个数字输出引脚&#xff0c;可在 0V 和 3.3V 或 5V 之间…
阅读更多...
《向量数据库指南》：使用公共的Pinecone数据集

《向量数据库指南》：使用公共的Pinecone数据集

目录 数据集包含向量和元数据 列出公共数据集 加载数据集 迭代数据集 分批迭代文档并插入到索引中。 将数据集插入为数据帧。 接下来怎么做 本文档介绍如何使用现有的Pinecone数据集。 要了解创建和列出数据集的方法，请参阅创建数据集。 数据集包含向量和元数据 P…
阅读更多...
WPF 搜索框控件样式

WPF 搜索框控件样式

WPF 搜索框控件样式 完全通过Xaml代码实现&#xff0c;使用了UserControl进行封装。功能包括聚焦时控件展开&#xff0c;输入为空时的文字提示&#xff0c;以及待选提示项列表等效果。实现效果如下图&#xff1a; xaml代码 <UserControl x:Class"SearchBar.SearchBo…
阅读更多...
栈OJ（C++）

栈OJ（C++）

文章目录 1.最小栈2.栈的压入、弹出序列3.逆波兰表达式&#xff08;后缀表达式&#xff09;求值3.1后缀表达式求值3.2中缀表达式转后缀表达式3.3带有括号的中缀表达式转后缀表达式 1.最小栈 class MinStack { public:MinStack(){}void push(int val){_st.push(val);//empty放在…
阅读更多...
【kafka调试】用命令行查看kafka是否发出了命令

【kafka调试】用命令行查看kafka是否发出了命令

server 10.10.90.210:9092 topic stream_manager_center_capture_file 摄像头id&#xff1a; 17283ed2a1ac685f9fd5ef9f0de04792 cd /usr/loca/kafka bin/kafka-console-consumer.sh --bootstrap-server 10.10.90.210:9092 --topic stream_manager_center_capture_file 然后添…
阅读更多...
＜C语言＞ 数据在内存中的存储

＜C语言＞ 数据在内存中的存储

1.数据类型介绍 C语言中的基本内置类型如下&#xff1a; char //字符数据类型 short //短整型 int //整型 long //长整型 long long //更长的整型 float //单精度浮点数 double //双精度浮点数类型的意义&#xff1a; 1.使用这个类…
阅读更多...
设计模式-抽象工厂模式

设计模式-抽象工厂模式

在经济学领域中&#xff0c;其主要研究对象(商品)之间根据消费依存关系可分为互补商品或替代商品&#xff0c;其中&#xff0c;互补商品如汽车与汽油、自行车与自行车胎、大饼和香肠、开水和泡面等。在面向对象的代码世界中&#xff0c;不同对象之间也存在这种类似相互依赖的关…
阅读更多...
使用 ChatGPT 碰到的坑

使用 ChatGPT 碰到的坑

最近在使用 ChatGPT 的时候碰到一个小坑&#xff0c;因为某些特殊情况我需要使用 syslog 向 logbeat 中发送日志。 由于这是一个比较古老的协议&#xff0c;确实也没接触过&#xff0c;所以就想着让 ChatGPT 帮我生成个例子。 原本我已经在 Go 中将这个流程跑通&#xff0c;所…
阅读更多...
PyTorch从零开始实现Transformer

PyTorch从零开始实现Transformer

文章目录 自注意力Transformer块编码器解码器块解码器整个Transformer参考来源全部代码&#xff08;可直接运行&#xff09; 自注意力 计算公式 代码实现 class SelfAttention(nn.Module):def __init__(self, embed_size, heads):super(SelfAttention, self).__init__()self.e…
阅读更多...
ElasticSearch学习--RestClient及案例

ElasticSearch学习--RestClient及案例

目录 RestClient查询文档 快速入门 总结 全文检索&#xff08;match&#xff09;查询 精确查询 复合查询 查询总结 排序&#xff0c;分页 高亮 RestClient查询文档 快速入门 总结 全文检索&#xff08;match&#xff09;查询 多种查询的差异都在做类型和条件上&#x…
阅读更多...
数据可视化——如何绘制地图

数据可视化——如何绘制地图

文章目录 前言如何绘制地图添加配置项 根据已有数据绘制地图整体代码展示 前言 前面我们学习了如何利用提供的数据来对数据进行处理&#xff0c;然后以折线图的形式展现出来&#xff0c;那么今天我将为大家分享如何将提数据以地图的形式展现。 如何绘制地图 前面我们绘制折线…
阅读更多...
如何从gitee上下载项目并把它在本地运行起来

如何从gitee上下载项目并把它在本地运行起来

有时候我们会想到在gitee上下载下来项目&#xff0c;那么怎么把项目下载到本地并跑起来呢&#xff1f; 第一步&#xff1a;在git上找到你想要克隆下来的项目&#xff0c;按照如下操作复制项目地址连接&#xff0c;如下图&#xff1a; 以上可以选择HTTPS和SSH两种形式。 第二步…
阅读更多...
REST和RPC的区别

REST和RPC的区别

1 REST REST 不是一种协议&#xff0c;它是一种架构。大部分REST的实现中使用了RPC的机制&#xff0c;大致由三部分组成&#xff1a; method&#xff1a;动词&#xff08;GET、POST、PUT、DELETE之类的&#xff09;Host&#xff1a;URI&#xff08;统一资源标识&#xff09;&…
阅读更多...
jmeter压测过程中，ServerAgent响应异常：Cannot send data to network connection

jmeter压测过程中，ServerAgent响应异常：Cannot send data to network connection

ServerAgent异常信息&#xff1a; Cannot send data to network connection&#xff08;无法将数据发送到网络连接&#xff09; 原因&#xff1a; linux 防火墙 拦截了当前端口 解决方案&#xff1a; Linux 执行以下命令 /sbin/iptables -I INPUT -p tcp --dport 4445 -j ACC…
阅读更多...
数学建模入门-如何从0开始，掌握数学建模的基本技能

数学建模入门-如何从0开始，掌握数学建模的基本技能

一、前言 本文主要面向没有了解过数学建模的同学&#xff0c;帮助同学们如何快速地进行数学建模的入门并且尽快地在各类赛事中获奖&#xff0c;或者写出优秀的数学建模论文。 在本文中&#xff0c;我将从什么是数学建模、数学建模的应用领域、数学建模的基本步骤、数学建模的技…
阅读更多...
【动手学深度学习】--12.深度卷积神经网络AlexNet

【动手学深度学习】--12.深度卷积神经网络AlexNet

文章目录 深度卷积神经网络AlexNet1.AlexNet2.模型设计3.激活函数4.模型实现5.读取数据集6.训练AlexNet 深度卷积神经网络AlexNet 学习视频&#xff1a;深度卷积神经网络 AlexNet【动手学深度学习v2】 官方笔记&#xff1a;深度卷积神经网络&#xff08;AlexNet&#xff09; …
阅读更多...
Android 中 app freezer 原理详解(一)：R 版本

Android 中 app freezer 原理详解(一)：R 版本

基于版本&#xff1a;Android R 0. 前言 在之前的两篇博文《Android 中app内存回收优化(一)》和 《Android 中app内存回收优化(二)》中详细剖析了 Android 中 app 内存优化的流程。这个机制的管理通过 CachedAppOptimizer 类管理&#xff0c;为什么叫这个名字&#xff0c;而不…
阅读更多...
【Linux | Shell】结构化命令2 - test命令、方括号测试条件、case命令

【Linux | Shell】结构化命令2 - test命令、方括号测试条件、case命令

目录 一、概述二、test 命令2.1 test 命令2.2 方括号测试条件2.3 test 命令和测试条件可以判断的 3 类条件2.3.1 数值比较2.3.2 字符串比较 三、复合条件测试四、if-then 的高级特性五、case 命令 一、概述 上篇文章介绍了 if 语句相关知识。但 if 语句只能执行命令&#xff0c…
阅读更多...
Docker 的数据管理、容器互联、镜像创建

Docker 的数据管理、容器互联、镜像创建

目录 一、数据管理 1.数据卷 2. 数据卷容器 二、容器互联&#xff08;使用centos镜像&#xff09; 三、Docker 镜像的创建 1.基于现有镜像创建 1.1首先启动一个镜像&#xff0c;在容器里修改 1.2将修改后的容器提交为新的镜像&#xff0c;需使用该容器的id号创建新镜像 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023