三维green公式_Green、Gauss、Stokes公式

Green公式的引子

设

为平面上的一个区域，如果

内的任意一条封闭曲线都可以不经过

外的点连续地收缩到

中的一点，那么

称为

单连通区域，否则为复连通区域。简单地说就是若区域

中没有“洞”，则为单连通区域，否则为复连通区域，如下图所示：

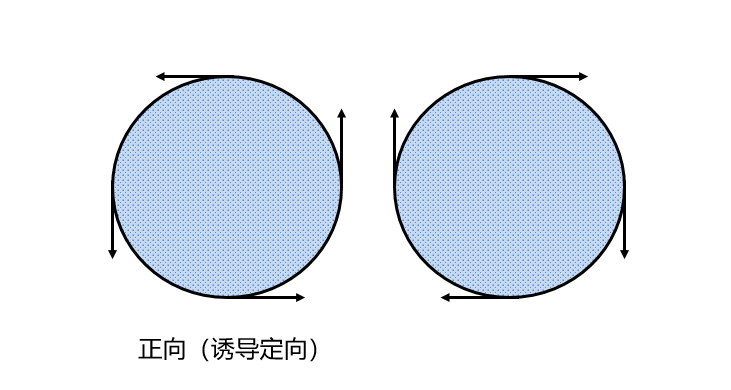
对于一个区域

，给它的边界

规定一个正向：若一个人沿着边界

行走，

总在他的左边，则称此人行走的方向为

的正向，亦称诱导定向，带有这样定向的边界

称为

的正向边界，示意图如下：

左边的逆时针方向为D的正向（诱导定向）

Green公式

设

为平面上由光滑或分段光滑的简单闭曲线所围的单连通区域（可推广到具有有限个“洞”的复连通区域上）。若函数

在

上具有连续偏导数，则：

其中

取正向，即诱导定向。

对于有有限个“洞”的复连通区域，可将区域作有限个分割，使其成为有限个单连通区域的叠加，每两个相邻单连通区域的公共曲线部分，边界的方向恰好相反，从而对该曲线的积分为0，故而Green公式对有有限个“洞”的复连通区域亦成立（这一点可参考:格林公式如何推广到有有限个“洞”的复连通区域上？）。

说明：

1.Green公式说明了有界闭区域上的二重积分与沿区域边界的第二类曲线积分的关系。

2.Green公式还可表示为如下方便记忆的形式：

3.Green公式是Newton-Leibniz公式的推广。

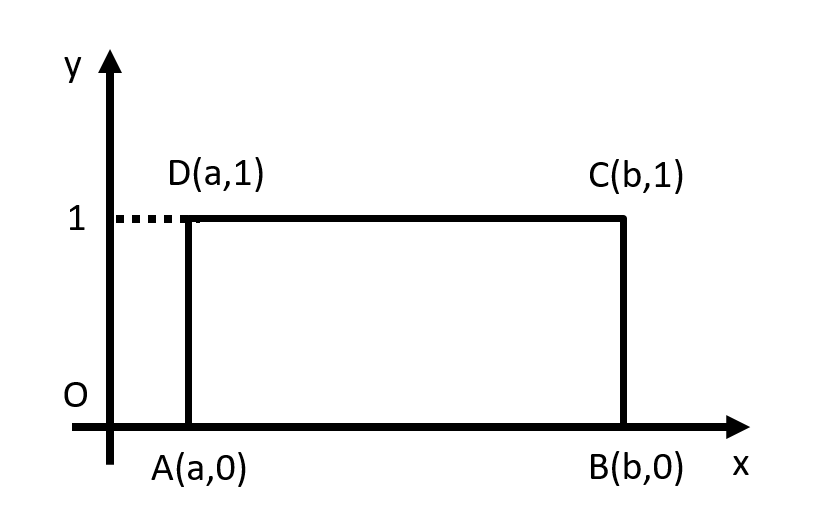
设

在

上具有连续导数，取

（见上图）。在Green公式中取

，即得

将左边化为累次积分：

而右边等于

因为在

和

段，

，上式继而等于

即得Newton-Leibniz公式。

4.可利用Green公式求区域面积。

设

平面上的有界闭区域，其边界为分段光滑的简单闭曲线，则它的面积：

曲线积分与路径无关的条件：Green定理

定义：设

为某平面区域，

为

上的连续函数。若对

内任意两点

，积分值

只与

点的位置有关，而与从

到

的路径

无关，则称曲线积分

与

路径无关。

Green定理:

设

为平面上的单连通区域，

在

上具有连续偏导数，则下面四个命题等价：

1.曲线积分

与路径无关。

2.对于

内任意一条光滑（或分段光滑）闭曲线

：

3.存在

上的可微函数

，使得：

即

为

的全微分，此时

称为

的

原函数。

4.在

内成立：

Green定理与常微分方程中的恰当方程的解法有相通之处，关于恰当方程的解法，可参见：初等积分法之恰当方程形式 - coffee的文章

Gauss公式引子

设

为空间上的一个区域。如果

内的任何一张封闭曲面所围的立体仍属于

,那么称

为

二维单连通区域，否则称

为

二维复连通区域。简单地说，二维单连通区域之中不含有“洞”,而二维复连通区域之中含有“洞"。例如，单位圆球

是二维单连通区域，而空心球

是二维复连通区域。如下图。

同二维区域

边界

的

诱导定向，亦可通俗地定义三维区域

边界

的

诱导定向：若一个人沿

行走，

始终在他的脚下，也即他始终在

外面，这里所谓的“外面”即为边界

的正向，即

诱导定向。

Gauss公式

设

是上由分段光滑（或分片光滑）的封闭曲面所围成的二维单连通区域（可推广到具有有限个“洞”的二维复连通区域上），函数

在

上具有连续偏导数，则成立：

这里

的定向为外侧，即

诱导定向。

说明：

1.Gauss公式说明了在空间中一个区域

上的三重积分与沿其边界

的曲面积分间的内在关系，可视为Green公式的一个推广。

2.可利用Gauss公式求一个区域

的体积：

其中

的定向为外侧，即

诱导定向。

Stokes公式引子

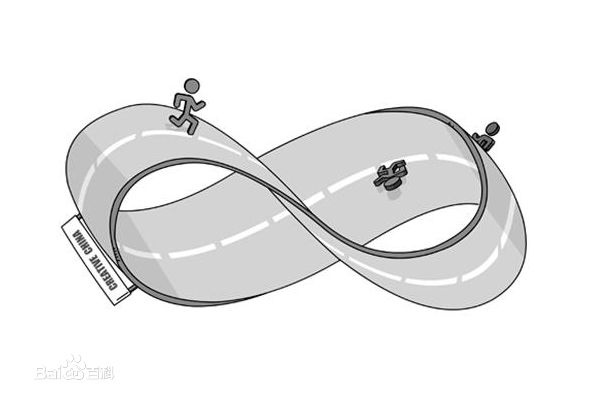
双侧曲面，用以区分单侧曲面，典型的单侧曲面的例子是莫比乌斯带。莫比乌斯带上的人不用穿过带子就可以达到带上的任意一点，而双侧曲面不具有这样的性质。我们可以简单地理解，双侧曲面就是具有内外两个方向的曲面，严格的定义见教材。

莫比乌斯带（来源见水印）

设

为具有分段光滑边界的非封闭光滑

双侧曲面。选定曲面的一侧，并如下规定

的边界

的一个正向：如果一个人保持与曲面选定一侧的法向量同向站立，当他沿

的这个方向行走时，曲面

总是在他左边。

的这个定向也称为

的

诱导定向，这种定向方法称为右手定则。

Stokes公式

设

为光滑曲面，其边界

为分段光滑闭曲线。若函数

在

及其边界

上具有连续偏导数，则成立：

这里

为

诱导定向，

为曲面微元

上的方向向量。

说明：

1.Stokes公式说明了沿曲面

的曲面积分与沿其边界

的曲线积分间的内在关系，它也是Green公式的一个自然推广。

2.Stokes公式还可表示为如下方便记忆的形式：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/573896.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！