目录
- 电阻性电路分析
- 第三章 电路分析方法
- 3-1 支路电流法
- 3-2 网孔电流法
- 3-3 节点电位法
- 3-4本章总结
- 第四章 电路定理
- 4-1 叠加定理
- 戴维南定理和诺顿定理
- 第三章 电路分析方法
电阻性电路分析
声明:本学习笔记中的部分图片来自于王丽华老师的PPT,感想王老师~~
第三章 电路分析方法
一般分析方法:可求解任意电路的所有支路电压和电流
等效电路法:只适用于简单电路,且只能分析某一些支路的电压和电流
分析的中心任务:
- 如何选择分析电路的变量
- 如何建立相应的独立方程
3-1 支路电流法
- 基于电路支路电流,利用KCL、KVL和元件的VCR,以电路各支路电流作为变量,分别对节点和回路列出方程。 注意:参考方向一经确定就不能更改!
- 步骤:
- 由电路的支路数m,确定待求的支路电流数
- 根据节点数n,可以列出n-1个独立的KCL节点方程(流入为正,流出为负)
- 根据KVL列出回路方程。选取l=m-(n-1)个独立的回路(所有网孔),选定回路方向(顺时针方向),由KVL列出l个独立方程
- 将独立方程联立求解,得各支路的电流。如果支路电流值为正,则表明实际电流方向一参考方向相同;如果某一支路的电流为负,则表示实际电流的方向与参考方向相反。
- 根据电路的要求,求出其他待求量,如支路或元件上的电压、功率等。
- 注:求各电阻上吸收的功率,电阻包括电源!
- 步骤:
3-2 网孔电流法
- 以网孔电流作求解电路的未知量
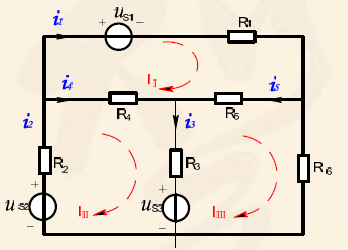
- 网孔电流是一种假象沿着各自网孔内循环流动的电流,如图所示:设网孔I的电流为iI;网孔II 的电流为iII ;网孔III的电流为i III ;网孔电流在实际中是不存在的。但它是一种很有用的用于计算的量。选中图中电路的支路电流参考方向,则有:
- 各网孔电流方程中,本网孔电流的系数为本网孔电阻之和,称为自电阻;其他网孔电流的系数表示本网孔与其他网孔公共支路上的电阻,称为互电阻,用R加下角标本网孔和其他网孔的数字表示,如下图中的R12,R13...互电阻的正负根据所在网孔的电流方向是否相同判断,相同为正,不同为负

自电阻×本网孔电流±Σ互电阻×相邻网孔电流
=本网孔所含电压源的代数和- 所设定的所有网孔参考方向均相同
- 先求一般方程需要的参数,联立求解一般方程,最后选取最大回路列KVL检验结果是否正确
注:使用时列一般方程不用考虑电流源,依据电流源可以列出额外方程
3-3 节点电位法
- 在电路中任意选择一个节点为非独立节点,称此节点为参考点.其它独立节点与参考点之间的电压,称为该节点的节点电压.
- 节点电压法是以节点电压为求解电路的未知量,利用基尔霍夫电流定律和欧姆定律导出(n-1)个独立节点电压为求知量的方程,联立求解,得出各节点电压.然后进一步求出各待求量
- 节点电压法适用于结构复杂、非平面电路、独立回路选择麻烦、以及节点少、回路多的电路的分析求解。对于n个节点、m条支路的电路,节点电压法仅需(n-1)个独立方程,比支路电流法少[m-(n-1)]个方程
- 列出的节点方程中,与本节点相连的所有支路电导之和成为自电导,恒为正值,G11,G22...,节点之间的电导称为互电导,恒为负值,G12,G13...
is1,is2是流向节点1的理想电流源电流的代数和,流入取正,流出取负 - 两个独立节点电路的节点电压方程的一般表达式:
- 自电导 ×本节点电压 -∑互电导 ×相邻节点电压
=流入本节点的电流源代数和
注:如果是电压源与电阻串联,"+"极靠近节点的电流取正,否则取负。电流大小为电压源的电压与其串联的电阻之比
ps:与电压源(独立源或受控源)相连的节点直接就是电源的电压
PS':节点电流法中方程里的电阻、电源都是与节点直接相连的(可以跨过电源)(因为不直接相连的都要通过直接相连的来对节点电位产生影响) - 归纳步骤
- 指定电路中某一节点为参考点,标出各独立节点电位(符号);
- 按照节点电压方程的一般形式,根据实际电路直接列出各节点电压方程
- 求解方程组,即可得出 各节点电位值
- 设定各支路电流的参考方向,根据欧姆定律和各节点电位值即可求出各支路电流
3-4本章总结
- 网孔电流法实际上是回路电流法选取网孔电流作为回路电流的解题方法。由于避免了列写节点电流方程,因而网孔电流计算相对简化(网孔内独立电源化为电压源,支路用电阻计算更方便)
- 一般情况下用网孔电流法比较简便,但在公共支路有电流源等特殊情况下,宜采用支路电流法
- 节点较少而网孔较多的电路,宜采用节点电位法求解(节点各支路独立电源化为电流源,支路用电导计算更方便)
第四章 电路定理
4-1 叠加定理
- 叠加定理是关于线性电路的一个重要性质的定理。
- 齐次性和叠加性
- 齐次性:在线性电路中,当只有一个独立源作用时,任一支路的响应(电压或电流)与独立源的激励成正比,即
y=kx\y-响应\x-激励\k-常数 - 叠加性:当线性电路中有两个或两个以上独立源作用时,任一支路的响应等于各个独立源单独作用下,分别在该支路上所产生的响应的代数和,即
y=k_1x_1+k_2x_2+...+k_nx_n\ki—从激励xi响应y的传输比,为常数 - (us单独作用下的响应)+(is单独作用下的响应)=( us、is共同作用下的响应)
将上述结论推广到一般线性网络中,就是叠加定理的内容 - 应用步骤:
- 将含有多个电源的电路,分解成若干个仅含有单个电源的分电路.并给出每个分电路的电流或电压的参考方向.在考虑某一电源作用时,其它的理想电源应置为零,即理想电压源短路;理想电流源开路
- 对每一个分电路进行计算,求出各相应支路的分电流、分电压
- 将求出的分电路中的电压、电流进行叠加,求出原电路中的支路电流、电压
- 叠加是代数量相加,当分量与总量的参考方向一致,取“+”;与总量的参考方向相反,则取“-”号
- 注意:
- 在计算某个独立源单独作用下的响应时,其它独立源取零值,即将其它的独立源电压源短路;独立电流源开路,而与这些独立源相连接的电阻、受控源或其它元件仍应保留
- 叠加定理只能用于计算响应量是电压或电流的情况,不能用于计算功率和能量
- 只适用于线性电路
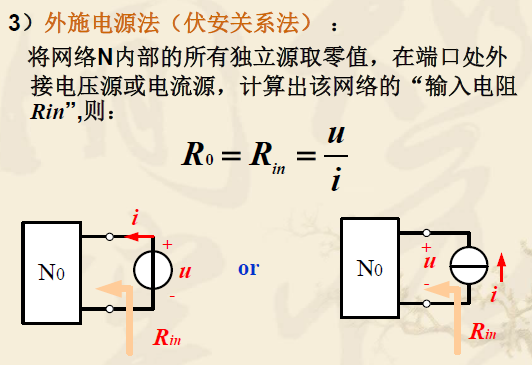
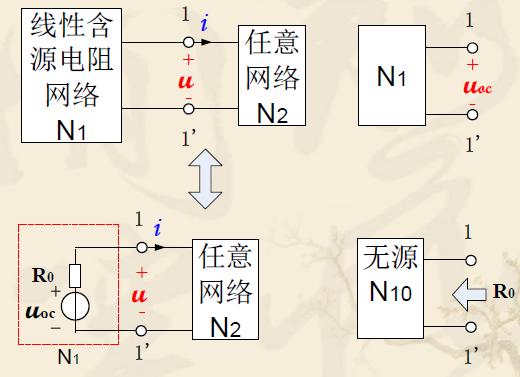
戴维南定理和诺顿定理
- 电流源开路,电压源短路

- 叠加定理适用于任一线性网络,包括时变的。定理指出:如果一个线性网络同时受若干独立电源的作用,则这些电源同时作用下的响应等于每个电源单独作用于网络的响应之和
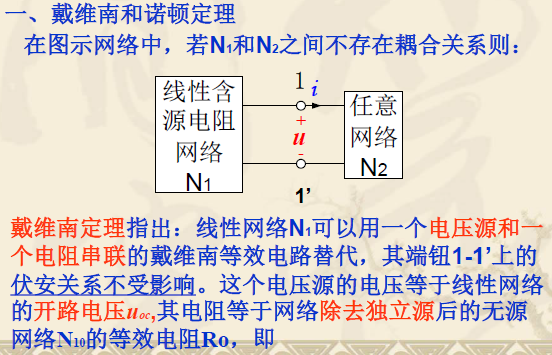
- 戴维南定理可用于任一线性网络。定理指出:如果任一线性网络在其两个端点上连接一个任意负载,则当进行下列任何一种置换时,负载上的电压及电流不变
- 由一个独立电压源和一个电阻串联组合所置换
- 由一个独立电流源和一个电阻并联组合所置换
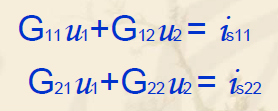







: Your password does not satisfy the current policy requirements)







)

)


![[中山市选]杀人游戏 (Tarjan缩点)](http://pic.xiahunao.cn/[中山市选]杀人游戏 (Tarjan缩点))