[中山市选]杀人游戏 (Tarjan缩点)

题目链接

Solution

可以考虑到如果知道环内一点的身份,如果凶手在其中就查出来了,同时不会有危险.
那么对警察造成威胁的就是那些身份不明且不能从其他点转移过来的点.
那么大部答案就是缩完点之后入度为 \(0\) 的联通块数量.
但是,会有特殊情况: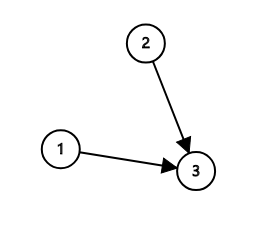

如图,我们就只要查 \(2\) 或者 \(1\) 其中的一点即可.
也就是说如果一个联通块仅包含一个点,且其出边所到的点都能由其他点推导出来.
那么我们可以通过调整对于入度为 \(0\) 的点的访问顺序以忽略这个点.
同时这样的点只能有一个(可以很简单举出反例).

Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000008;
struct sj{int to,next;}a[maxn];
int head[maxn],size,flagg;
int dfn[maxn],low[maxn];
int sta[maxn],top,belong[maxn];
int cnt,tot,v[maxn],n;
int du[maxn],ans,num,m;
int fr[maxn],to[maxn],siz[maxn];
void add(int x,int y)
{a[++size].to=y;a[size].next=head[x];head[x]=size;
}void tarjan(int x)
{dfn[x]=low[x]=++tot;sta[++top]=x;v[x]=1;for(int i=head[x];i;i=a[i].next){int tt=a[i].to;if(!dfn[tt]){tarjan(tt);low[x]=min(low[x],low[tt]);}else if(v[tt]) low[x]=min(low[x],dfn[tt]);}if(dfn[x]==low[x]){belong[x]=++cnt;v[x]=0;do{siz[cnt]++;belong[sta[top]]=cnt;v[sta[top]]=0;}while(sta[top--]!=x);}
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int x,y; scanf("%d%d",&x,&y);add(x,y);}for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);for(int x=1;x<=n;x++)for(int i=head[x];i;i=a[i].next){int tt=a[i].to;if(belong[tt]!=belong[x])du[belong[tt]]++,fr[++num]=belong[x],to[num]=belong[tt];}memset(a,0,sizeof(a));memset(head,0,sizeof(head));size=0;for(int i=1;i<=num;i++)add(fr[i],to[i]);for(int x=1;x<=cnt;x++)if(du[x]==0){ans++;if(siz[x]==1){int flag=1;for(int i=head[x];i;i=a[i].next){int tt=a[i].to;if(du[tt]==1){flag=0;break;}}if(!flagg)flagg=flag;if(!head[x])flagg=1;}}ans-=flagg;if(n==1)ans=0;if(m==0)ans=n-1;printf("%.6lf\n",(n*1.0-ans*1.0)/(n*1.0));
}