【数据结构】字符串匹配|BF算法|KMP算法|next数组的优化

字符串匹配算法是在实际工程中经常遇到的问题，也是各大公司笔试面试的常考题目，本文主要介绍BF算法（最好想到的算法，也最好实现）和KMP算法（最经典的）

一、BF算法

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和T的第二个字符，若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力法。 ---这段话来自百度百科

这段话晦涩难懂，需要例子支持。

下面我们就通过例子来解释这个问题。 l假定我们给出字符串“ababcabccabcacbab”作为主串，然后给出子串:“abcac”现在我们需要查找子串是否在主串中出现，出现返回主串中的第一个匹配的下标，失败返回-1;

1.图解：

2.代码实现：

思路：

分别用 i 和 j 来遍历主串和子串；

当主串和子串字符相同 i++ ，j++ ；

不同时 i = i - j +1 （i从下一个i开始继续遍历） j = 0（子串回到开头）；

直到 j >= lenSub (子串遍历完了）返回 i - j （主串中开始匹配的其实位置）

在Java中str == null和str.length == 0的区别：

str == null表示 str 没有指向任何对象，就是没有对应堆中对象

str.length() == 0表示 str 指向一个字符串对象，但是这个字符串长度为0

//str代表主串 sub代表子串public static int BF(String str, String sub) {if (str == null || sub == null) {return -1;}int lenStr = str.length();int lenSub = sub.length();if (lenStr == 0 || lenSub == 0) {return -1;}int i = 0;//遍历主串int j = 0;//遍历子串while (i < lenStr && j < lenSub) {if (str.charAt(i) == sub.charAt(j)) {i++;j++;} else {i = i - j + 1;j = 0;}}//子串遍历完了if (j >= lenSub) {return i - j;}return -1;}

二、KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特莫里斯一普拉特操作(简称KMP算法) 。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next( )函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)

---这段话来自百度百科

1. KMP算法解决的问题

对某些情况下的BF算法进行优化

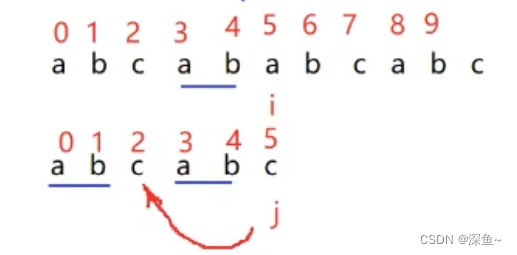
BF算法每次字符串匹配失败，子串的 j 都会回到子串的第一个字符，但是我们看下面这个图会发现在有些情况下这样的回退是没必要的：

当 i 和 j 都匹配到下标为5的字符时，发现主串和字串的字符不匹配，BF算法在此时就会将i 回退到主串下标1字符b，j回退到子串0下标重新进行匹配，既然是匹配到最后一个字符才失败，那么 i 前面和 j 前面一定有一部分是相同的，这里相同部分就是主串0，1和3，4下标都是ab字符串，我们发现此时 j 回退到2下标c位置重新开始合适，i 直接不回退

区别: KMP 和 BF 唯一不一样的地方在,我主串的 i 并不会回退，并且 j 也不会移动到 0 号位置，而是回退到一个特殊的位置

2.图解演示：

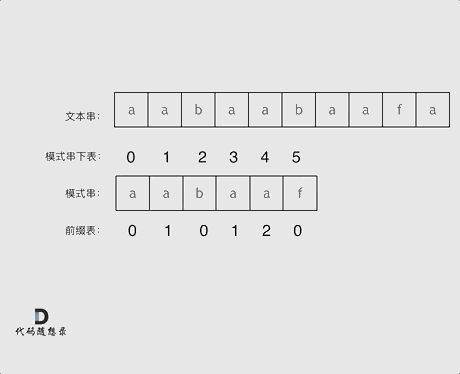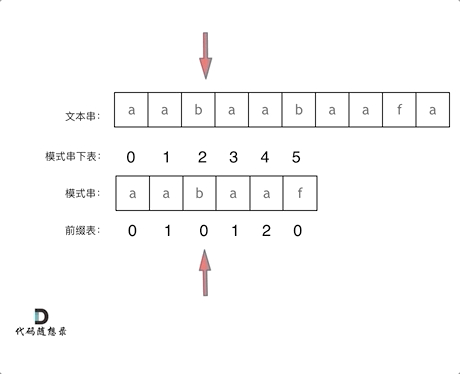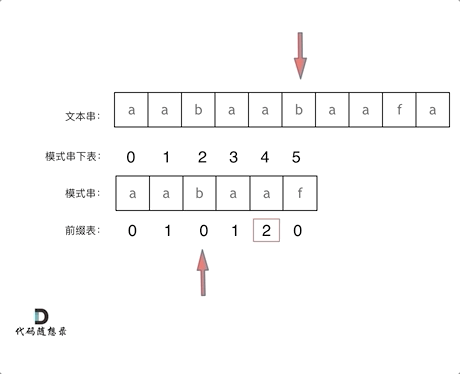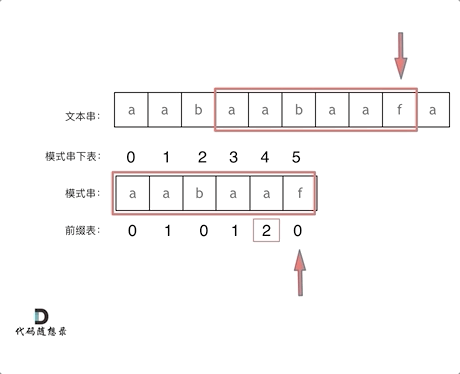
3. 为什么主串 i 不回退?

在下面这种情况下，在下标2位置匹配失败，i 即使回退到1位置也是没有必要的，因为 i回退到1位置的字符b 和子串下标0位置的字符a 也不一样

4. j 的怎么进行位置的回退——引出next数组

从上面KMP算法解决的问题可知：

此时匹配失败，我们不回退 i ，因为在这个地方匹配失败，说明 i 的前面和 j 的前面，是有部分是相同的，不然两个下标不可能走到这里来，所以 j 回退到2下标，i 不回退，这就是最好的情况

那么我们怎么知道 j 回退到哪个位置呢？由此引入了next数组

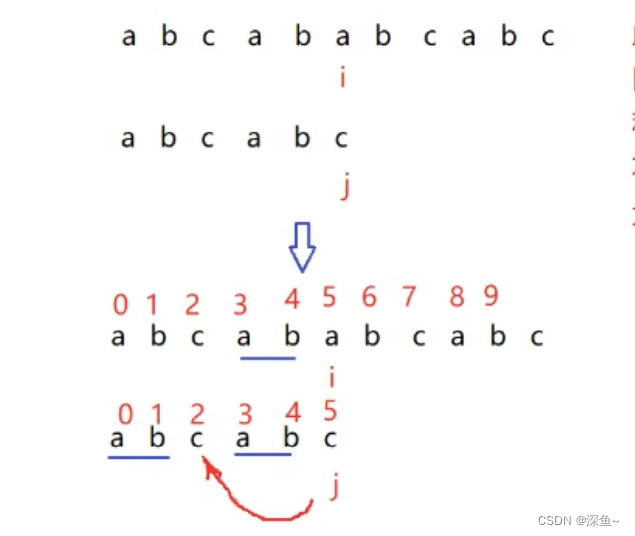
KMP 的精髓就是 next 数组: 这个数组用来保存某个位置匹配失败后，回退的位置

也就是用 next[ i ] = k来表示，不同的 i 来对应一个k值，这个 k 就是你将来要移动的i要移动的位置

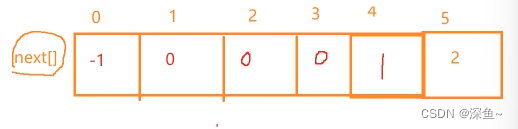
就拿上面的例子来说，j 回退到2下标那么next数组中 next [ 5 ] = 2

而 K 的值是这样求的（求next数组）:

(1) 规则: 在子串中找到匹配成功部分的两个相等的真子串(不包含本身)，一个以下标 0 开始，另一个以-1 下标结尾。
(2) 不管什么数据 next[0]= -1;next1]= 0;在这里，我们以下标来开始，而说到的第几个第几个是从 1 开始（也有些地方next[0]= 0;next1]= 1）

同样以上面的子串 abcabc 为例，求他的next数组：

下标0和下标1是固定的，那就不用说

下标2 ：j 处于下标2 ，我们就看有没有一个字符串以下标0（a字符）开始，另一个字符串以下标 -1（b字符）结束的两个相同的字符串 ab这三个字符中肯定没有所以next [2] = 0

下标3：j 处于下标3 ，我们就看有没有一个字符串以下标0（a字符）开始，另一个字符串以下标 -1（c字符）结束的两个相同的字符串 abc这三个字符中肯定没有所以next [3] = 0

下标4：j处于下标4，我们同样看有没有一个字符串以下标0（a字符）开始，另一个字符串以下标 -1（a字符）结束的两个相同的字符串 abca这三个字符中是有相同字符串a的所以next [4] = 1（这里的1代表相同字符串的长度,没有就为0）

下标5 ：j处于下标5 abcab 中ab 为相同的(一个a开头另一个b结尾)字符串所以next [5] = 2

求next数组的练习: 跟上面的过程一样，如果不懂可以去看博哥视频讲解的KMP算法 30min的位置

练习 1: 举例对于”ababcabcdabcde”，求其的 next 数组?

答案： -10012012001200

练习 2: 再对”abcabcabcabcdabcde”,求其的 next 数组?

答案： -10001 2345678901230

一般情况答案都是next[0]= 0;next1]= 1，所以我们在此答案基础上全部+1即可

从上面的答案我们可以得出结论：数组在增的时候都是一个一个+1，不可能跳着加

到这里大家对如何求next数组应该问题不大了，接下来的问题就是 :

5.已知next[ i ] = k;怎么求next[i+1]=?

如果我们能够通过 next [ i ]的值,通过一系列转换得到 next [ i+1]得值，那么我们就能够实现这部分

首先假设: next[ i ] = k 成立 (为了方便数组名命名为p）

那么，就有这个式子成立:p [ 0 ]...p [ k-1 ] = p [ x ] ..p [ i-1 ]

因为 i -1 -k = k -1 那么 x = i - k ，也就是p [ 0 ]...p [ k-1 ] = p [ i - k ] ..p [ i-1 ]

到这一步: 我们再假设如果 p [ k ] = p [ i ] ;在上面得到的式子两边加上这个式子
我们可以得到p [ 0 ]...p [ k ] = p [ i-k ] ..p [ i ] ;那这个就是 next[ i+1]= k+1;

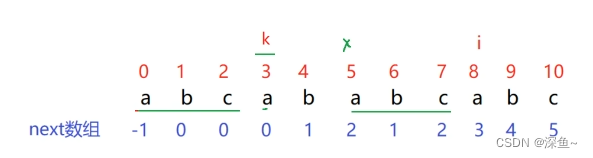
那么: p[ i ] != p[ k ] 呢?

看如下实例:

一次不匹配，j 回退到 2下标位置不一定是你要找的

继续回退此时回退到了0下标（也就是说 k一直回退去找 p [i] == p [k] ,这样就满足了p [ k ] = p [ i ])

6.KMP算法代码实现

//找到子串在主串当中的下标public static int KMP(String str,String sub,int pos) {if(str == null||sub == null) return -1;int lenStr = str.length();int lenSub = sub.length();if(lenStr == 0||lenSub == 0) return -1;if(pos<0 || pos >= lenStr) return -1;int [] next = new int[lenSub];getNext(sub,next);int i = pos;//从pos位置开始遍历主串int j = 0;//遍历子串while(i < lenStr && j <lenSub) {//这里要考虑到一开始就不匹配，j=-1if (j==-1||str.charAt(i) == sub.charAt(j)) {i++;j++;} else {//下标不一样，一直回退j = next[j];}}if(j==lenSub) {return i-j;}return -1;}//重点：求子串的next数组public static void getNext(String sub,int [] next) {next[0] = -1;next[1] = 0;int i = 2;//i表示所求next数组的下标，是提前走了一步的int k = 0;//比较是否相等的前一项的k//这里next[i]就是要求的，和我们分析的next[i+1]一样// 原来判断的是p[i]==p[k]，现在应该判断p[i-1]==p[k]while(i < sub.length()) {//此处要考虑k回退到了-1位置，next值就为0if (k==-1||sub.charAt(i-1) ==sub.charAt(k)) {next[i] = k+1;k++;i++;} else {//p[i-1]！=p[k]，则k继续回退k = next[k];}}}

7.next数组的优化

为什么要对next数组进行优化？

有如下串:aaaaaaaab,他的 next 数组是-1,0,1,2,3,4,5,6,7

假设5位置匹配失败，那么就得回退到4位置，4位置和5位置都是a，那么还得回退到3位置，而3位置和4位置都是a，还得继续回退，就这样一直回退到0位置，由此引入了nextval数组进行了优化

next 数组的优化，即如何得到 nextval 数组:

（1）回退到的位置和当前字符一样，就写回退那个位置的nextval值

（2）如果回退到的位置和当前字符不一样，就写当前字符原来的next值

就以上面字符串为例：

0下标：肯定还是为-1

1下标：这个位置回退到0位置，因为这个位置的值和0位置（回退的位置）的值一样，所以这个位置的值就写回退位置的值（即-1）

2-7下标：这些位置回退到前一个位置，值都是一样的，所以都是-1

8下标: 回退到的位置和当前字符不一样，直接写next[ 8 ]的值7即可

则修正后的数组 nextval 是:-1， -1，-1，-1， -1， -1， -1， -1，7。