Softmax的含义:Softmax简单的说就是把一个N*1的向量归一化为(0,1)之间的值,由于其中采用指数运算,使得向量中数值较大的量特征更加明显。

如图所示,在等号左边部分就是全连接层做的事。
- W是全连接层的参数,我们也称为权值;W是全连接层的参数,是个T*N的矩阵,这个N和X的N对应,T表示类别数,比如你进行手写数字识别,就是10个分类,那么T就是10。
- X是全连接层的输入,也就是特征。从图上可以看出特征X是N1的向量,他就是由全连接层前面多个卷积、激活和池化层处理后得到的;
举一个例子,假设全连接层前面连接的是一个卷积层,这个卷积层的输出是64个特征,每个特征的大小是7X7,那么在将这些特征输入给全连接层之前会将这些特征通过tf.reshape转化为成N1的向量(这个时候N就是64X7X7=3136)。
我们所说的训练一个网络,对于全连接层而言就是寻找最合适的W矩阵。因此全连接层就是执行WX得到一个T1的向量(也就是图中的logits[T1]),这个向量里面的每个数都没有大小限制的,也就是从负无穷大到正无穷大。然后如果你是多分类问题,一般会在全连接层后面接一个softmax层,这个softmax的输入是T1的向量,输出也是T1的向量(也就是图中的prob[T*1],这个向量的每个值表示这个样本属于每个类的概率),只不过输出的向量的每个值的大小范围为0到1。
softmax函数,或称归一化指数函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量A “压缩”到另一个K维实向量 A' 中,使得A' 每一个元素的范围都在(0,1)之间,并且所有元素的和为1。
该函数的形式可以按下面的式子给出:

可能大家一看到公式就有点晕了,别被吓跑,我来简单解释一下。这个公式的意思就是说得到的A'向量中的每个元素的值,是由A中对应元素的指数值除以A中所有元素的指数值的总和。
举个例子:假设你的A =[1,2,3],那么经过softmax函数后就会得到A' = [0.09, 0.24, 0.67],A'的三个元素分别是怎么来的呢?
A'的第1个元素 = exp(1) / (exp(1) + exp(2) + exp(3)) = 0.09(这里exp即为e)
A'的第2个元素 = exp(2) / (exp(1) + exp(2) + exp(3)) = 0.24
A'的第3个元素 = exp(3) / (exp(1) + exp(2) + exp(3)) = 0.67
由于Softmax函数的这个特点,经常会被用在神经网络来解决分类问题中,得到的结果就可以认为是满足各种分类的概率。
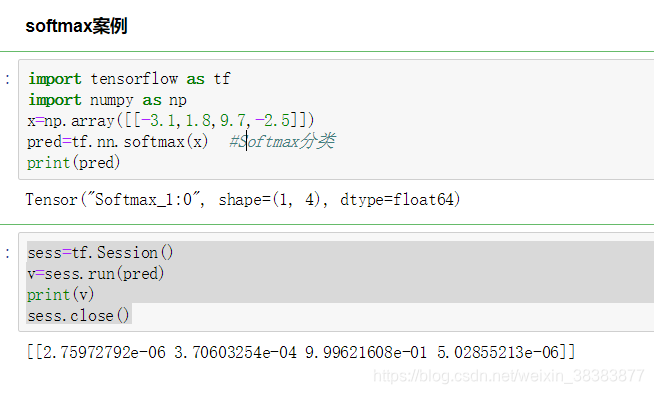

弄懂了softmax,就要来说说softmax loss了。
那softmax loss是什么意思呢?如下:
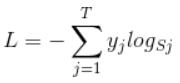
首先L是损失。Sj是softmax的输出向量S的第j个值,前面已经介绍过了,表示的是这个样本属于第j个类别的概率。yj前面有个求和符号,j的范围也是1到类别数T,因此y是一个1*T的向量,里面的T个值,而且只有1个值是1,其他T-1个值都是0。那么哪个位置的值是1呢?答案是真实标签对应的位置的那个值是1,其他都是0。所以这个公式其实有一个更简单的形式:
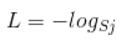
当然此时要限定j是指向当前样本的真实标签。
来举个例子吧。假设一个5分类问题,然后一个样本I的标签y=[0,0,0,1,0],也就是说样本I的真实标签是4,假设模型预测的结果概率(softmax的输出)p=[0.1,0.15,0.05,0.6,0.1],可以看出这个预测是对的,那么对应的损失L=-log(0.6),也就是当这个样本经过这样的网络参数产生这样的预测p时,它的损失是-log(0.6)。那么假设p=[0.15,0.2,0.4,0.1,0.15],这个预测结果就很离谱了,因为真实标签是4,而你觉得这个样本是4的概率只有0.1(远不如其他概率高,如果是在测试阶段,那么模型就会预测该样本属于类别3),对应损失L=-log(0.1)。那么假设p=[0.05,0.15,0.4,0.3,0.1],这个预测结果虽然也错了,但是没有前面那个那么离谱,对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数,而且log函数是递增函数,所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大,预测错得离谱比预测错得轻微的损失要大。
理清了softmax loss,就可以来看看cross entropy了。
corss entropy是交叉熵的意思,它的公式如下:
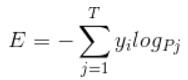
是不是觉得和softmax loss的公式很像。当cross entropy的输入P是softmax的输出时,cross entropy等于softmax loss。Pj是输入的概率向量P的第j个值,所以如果你的概率是通过softmax公式得到的,那么cross entropy就是softmax loss。
转载内容,根据自己理解稍作修改,原文连接为:
https://blog.csdn.net/u014380165/article/details/77284921
参考自:https://blog.csdn.net/wgj99991111/article/details/83586508
https://blog.csdn.net/kevindree/article/details/87365355



















和sizeof(数组名)的区别)