文章目录

特殊矩阵

矩阵的基本概念

求解线性方程组

直接求解

判定求解

特殊矩阵

零矩阵、1矩阵及单位矩阵

生成nxn方阵：

A=zeros(n), B=ones(n), C=eye(n)

生成mxn矩阵：

A=zeros(m,n), B=ones(m,n), C=eye(m,n)

生成和矩阵B同样位数的矩阵：

A=zeros(size(B))**

生成nxm阶标准均匀分布伪随机数矩阵(0-1)：

A=rand(n,m)

生成nxn阶标准均匀分布伪随机数方阵：

A=rand(n)

对角元素矩阵

已知向量生成对角矩阵：

A=diag(V)

已知矩阵提取对角元素列向量：

V＝diag(A)

生成主对角线上第k条对角线为V的矩阵：

A=diag(V,k)

生成n阶的Hilbert矩阵：

A=hilb(n)

求取逆Hilbert矩阵：

B=invhilb(n)

Hankel(汉克 ) 矩阵

其中：第一列的各个元素定义为C向量，最后一行各个元素定义为R。H为对称阵。

H1=hankel(C,R)

Vandermonde(范德蒙)矩阵

V = vander(C)

伴随矩阵

B = compan(P)

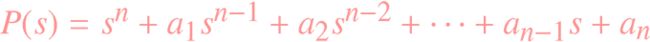
P(s)为首项系数为1的多项式

符号矩阵的输入,数值矩阵A转换成符号矩阵：

B=sym(A)

A =

1.0000 0.5000 0.3333

0.5000 0.3333 0.2500

0.3333 0.2500 0.2000

B=sym(A)

B =

[ 1, 1/2, 1/3]

[ 1/2, 1/3, 1/4]

[ 1/3, 1/4, 1/5]

矩阵的基本概念

求行列式

d=det(A)

矩阵的迹

t=trace(A)

矩阵的秩

r=rank(A) ％用默认的精度求数值秩

r=rank(A，a ) ％给定精度下求数值秩

如果 矩阵的秩为r，小于矩阵的阶次n，故为**非满秩矩阵**

矩阵范数

(p = 2, 2范数，向量的范数，各分量平方和开根号)

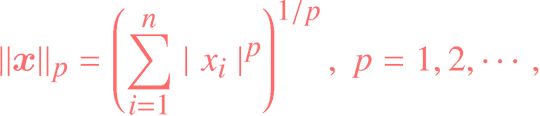
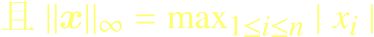
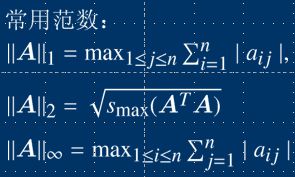
N=norm(A) ％求解默认的2范数

N=norm(A，选项) ％选项可为1,2,inf等

特征多项式

C=poly(A)

例：>> A=[16 2 3 13; 5 11 10 8; 9 7 6 12; 4 14 15 1];

poly(A) ％直接求取

ans =

1.0e+03 *

0.0010 -0.0340 -0.0800 2.7200 0.0000

A=sym(A); charpoly(A) ％运用符号工具箱

ans =

[ 1, -34, -80, 2720, 0]

矩阵的逆矩阵

C=inv(A)

hilb的逆矩阵

计算误差范数：

norm(H*inv(H)-eye(size(H))

对接近于奇异矩阵，高阶一般不建议用inv( )，可用符号工具箱

奇异矩阵不存在一个相应的逆矩阵，用符号工具箱的函数也不行

奇异矩阵与非奇异矩阵

矩阵的相似变换与正交矩阵

其中：A为一方阵，B矩阵非奇异。

相似变换后，X矩阵的秩、迹、行列式与特征值等均不发生变化，其值与A矩阵完全一致。

对于一类特殊的相似变换满足如下条件，称为正交矩阵。

正交基矩阵

Q = orth(A)

特征值

eig(A)

求解线性方程组

直接求解

A*X = B

左除：X= A\ B

% 反斜杠\反斜杠计算方法速度更快，

而且残差减少了几个数量级。err_inv 和 err_bs 均为 1e-6 的阶数。

X*A = B

右除：X= B/ A

判定求解

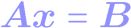
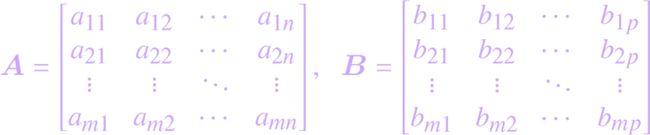
判定矩阵为C;

判定定理：

当m = n, rank (A)= rank ( C ) = n ,有唯一解。X = inv(A)*B

当rank (A)= rank ( C ) =r < n ,有无穷多解。

求取A矩阵的化零矩阵：

Z=null(A)

特解

x0=pinv(A)*B % 得出一个特解

通解：

syms a1 a2;

x=a1*Z(:,1)+a2*Z(:,2)+x0 %这里是r = 2, a1, a2 是随机数(数值解)，或者符号(解析解)

3.当rank (A)<= rank ( C ) ,只能用摩尔－彭罗斯广义逆求解出的方程最小二乘解不满足原始代数方程。

x = pinv(A)*B

后面会更新更高级的解法！

子曰：温故而知新