「数学期望——某件事情大量发生之后的平均结果」

----------------分割又分割----------------------

昨天文章排版出了问题，今天重新排版。

数据的三个统计维度：集中程度、离散程度、分布情况。

集中程度：期望

离散程度：方差、标准差

分布情况：曲线或者其他指标表示(偏态系数等等)

离散型概率分布常见的有：二项式分布、泊松分布分布。

「二项式分布」

二项式分布和二项式试验息息相关：

• 相互独立的一系列相同的n个试验组成：例如多次投硬币(互相独立，第一次投出的结果不会影响到第二次结果)

• 每次试验只有两种可能的结果，一个失败，一个成功(即一个正面，一个反面)

• 每次试验成功的概率都相同。投出正面的概率为0.5，反面也是0.5。

  

概率函数：

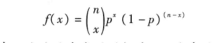
期望与方差：

「泊松分布」

   泊松试验(西蒙.泊松于1837年文章首先提到)：

• 在任意长度相等的区间上，事件发生的概率是相同的。

• 在任一区间上是否发生与事件在其他区间上是否发生是独立的。

概率函数：在一个区间内发生K次的概率，参数λ是单位时间(或单位面积)内随机事件的平均发生次数。e为数学常数，2.71828。

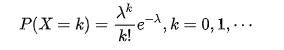
       期望与方差都是λ

       举例(来自教材)：我们假设任意两个长度相等时间段内有一辆汽车到达的概率是相同的。并且任一时间段上是否有汽车到达与其他时间是否有汽车到达互相独立。我们历史数据显示：15分钟内平均到达10辆车。

       那么我们要15分钟内恰好有5辆车到达的概率。

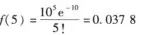
「拓展了解：超几何分布」

      超几何分布中的各次试验不是独立的；试验中成功的概率也是不等的。

例如不放回抽样调查。

      概率函数：x表示成功的次数，n表示试验次数。N为总体中元素个数，r代表总体中代表成功的元素个数。

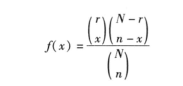
举例：

      已知在20件产品中有2件次品，18件正品。如果随机抽出3件，问抽到0件，1件和2件次品的概率各为多少？

      设X代表抽到次品的件数。因为在有限总体进行非重复抽样时，每次抽取的概率都会发生变化，所以用超几何分布。
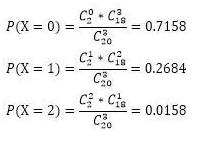