引言
编译器里的循环优化有两个重要的目标,一是提高局部性,二是提高并行性,loop tiling是提高数据局部性最重要的优化之一,是传统编译器和深度编译器考虑的重中之重,我们今天来看看如何做loop tiling(循环分块)(aka cache blocking)。
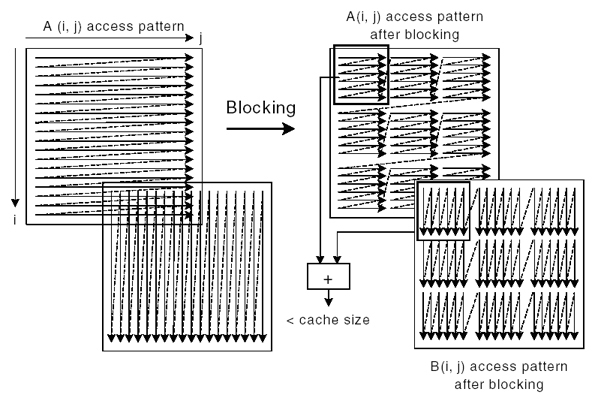
loop tiling的basic idea很简单,就是一个cache line现在被用过以后,后面什么时候还会被用,但是按循环默认的执行方式,可能到下次再被用到的时候已经被evict了。于是我们就把循环怎么重排一下,使得一个cache line在被evict之前就被再次使用。
在该文中我们讨论一个简单的tiling方法,以及通过计算cache miss来估算tiling的作用。
例程一
我们从一个简单的例子看起,为了更好的可读性,我们使用Fortran语法(column major):
DO I = 1, NDO J = 1, MA(I) = A(I) + B(J) END DO
END DO首先我们分析一下该循环的重用模式(reuse pattern),可以看到A(I)在每一轮J循环中被重用、B(J)在每一轮I循环中会被重用。当前由于I是外层循环,所以当B(J)在J层循环中的跨度太大时(无法fit in the cache),则在被下一次I重用时数据已被清出缓存。譬如我们假设M和N是很大的数(大数组),所以对于每一轮I循环,等到B(M)被访问时,B(1)、B(2)等已经被清出缓存了。
分析完了重用模式,我们现在计算cache miss。假设每个cache line能容纳b个数组元素,associativity是fully associative,则可计算出A的cache miss次数是N/b,B的cache miss次数是N*M/b。
现在我们来看看什么是tiling,以及如何通过做tiling减少cache miss。
我们先考虑tile J层循环,将B的访问模式变成如下,令tile size为T,T一般是b的倍数,也足够小,可以认为N,M >> b,T,T的取值应该使得当B(T)被访问时B(1)也依然还在缓存中:
I=1: B(1), B(2), B(3) ... B(T)
I=2: B(1), B(2), B(3) ... B(T)
I=3: B(1), B(2), B(3) ... B(T)
...
I=N: B(1), B(2), B(3) ... B(T)I=1: B(T+1), B(T+2), B(T+3) ... B(2T)
I=2: B(T+1), B(T+2), B(T+3) ... B(2T)
I=3: B(T+1), B(T+2), B(T+3) ... B(2T)
...
I=N: B(T+1), B(T+2), B(T+3) ... B(2T)小灯泡:tile的本质当总的数据量无法fit in cache的时候,把数据分成一个一个tile,让每一个tile的数据fit in the cache。所以tiling一般从最内层循环开始(tile外层循环的话一个tile就包括整个内层循环,这样的tile太大)。
此时循环变成:
DO J = 1, M, TDO I = 1, NDO jj = J, min(J+T-1, M)A(I) = A(I) + B(jj)END DOEND DO
END DO注意当我们tile J层循环的时候,tile以后J层循环就跑到了外层(loop interchange),这样又会影响A的缓存命中率。该变换又称为strip-mine-and-interchange。我们可以计算此时A的cache miss次数是(M/T) * (N/b),B的cache miss次数是T/b * M/T = M/b(每一轮J层循环miss一次),所以总共的cache miss是MN/(bT) + M/b,tile之前是N/b+N*M/b。所以在M和N的大小也相当的情况下做tiling大约能将cache miss缩小T倍。
思考题1:为什么分块以后还要交换循环I和J?循环交换是否总是可行的?
那要是我们选择tile I层循环呢?我们看看会发生什么。要tile I层循环首先将I、J循环调换:
DO J = 1, MDO I = 1, NA(I) = A(I) + B(J) END DO
END DO依然假设tile size=T,访问模式将变为:
J=1: A(1) B(1), A(2) B(1), A(3) B(1) ... A(T) B(1)
J=2: A(1) B(2), A(2) B(2), A(3) B(2) ... A(T) B(2)
...
J=M: A(1) B(M), A(2) B(M), A(3) B(M) ... A(T) B(M)J=1: A(T+1) B(1), A(T+2) B(1), A(T+3) B(1) ... A(2T) B(1)
J=2: A(T+1) B(2), A(T+2) B(2), A(T+3) B(2) ... A(2T) B(2)
...
J=M:A(T+1) B(M), A(T+2) B(M), A(T+3) B(M) ... A(2T) B(M)
...此时循环变成:
DO I = 1, N, TDO J = 1, MDO ii = I, min(I+T-1, N)A(ii) = A(ii) + B(J)END DOEND DO
END DO此时A的cache miss次数是T/b * N/T,B的cache miss次数是M/b*(N/T),加起来就是(MN)/(bT)+N/b,而tile J层循环得到的cache miss是(MN)* (bT)+M/b,所以对于该循环到底应该tile I层循环还是J层循环更好其实取决于M和N的相当大小。
思考题2:是否可以既tile I层循环也tile J层循环?如果可以,这样做是否具有更好的局部性?
例程二
DO J = 1, MDO I = 1, ND(I) = D(I) + B(I, J)END DO
END DO注:fortran是column major layout,B(I, J)是访问二维数组,相当于C语言中的B[I][J]。不管是column major还是row major不影响tiling的原理。
注:对于多维数组我们在计算cache miss时假设数据的存储是连续的。
该循环的cache miss是M*N/b + M*N/b(D和B的miss都是M*N/b)。
还是用之前的strip-mine-and-interchange方法来tile内层循环I:
DO I = 1, N, TDO J = 1, MDO ii = I, min(I+T-1, N)D(ii) = D(ii) + B(ii, J)END DOEND DO
END DOtiling loop I 之后的cache miss是N/T * T/b + T/b * M * N/T(J层循环每一轮一开始都会miss B)= N/b + NM/b。
再考虑tile J层循环(需要首先调换I、J层循环):
DO J = 1, M, TDO I = 1, NDO jj = J, min(J+T-1, M)D(I) = D(I) + B(I, jj)END DOEND DO
END DO此时的cache miss是N/b * M/T + T*(N/b)*M/T = NM/(bT) + MN/b。跟tiling I循环相比,由于M一般远大于T,所以会有更高的cache miss。造成这个区别的本质原因在于D(I)在J层的重用没有被exploited。
例程三
我们再来看一个更有趣的例子:矩阵转置。
DO J = 1, NDO I = 1, NA(I, J) = B(J, I)ENDDO
ENDDO这个例子之所以有趣是因为,无论是否做交换I、J循环(交换是合法的),cache miss都是N*N/b + N*N。下面是交换I、J循环后的情况:
DO I = 1, NDO J = 1, NA(I, J) = B(J, I)ENDDO
ENDDO如果I是内层循环,则A的miss是N*N/b,而B每次都是miss,所以一共miss N*N次。如果J是内层循环,则是A每次都是miss,而B miss N*N/b次。不管哪种情况,都有一个没有achieve locality。
那有什么办法让A和B都能achieve locality吗?答案是可以,请看如下的tiling:
DO I = 1, N, TDO J = 1, N, TDO ii = I, min(I+T-1, N)DO jj = J, min(J+T-1, N)A(ii, jj) = B(jj, ii)ENDDOENDDOENDDO
ENDDO这里的精髓在于tiling不仅可以利用temporal locality,也能用上spatial locality。对于A(ii, jj),虽然最内层循环是jj(没有locality),但是当内层循环jj完了以后开始下一轮ii的时候,因为tiling使得A(ii, jj)、A(ii, jj+1)依然会在缓存,于是这时的A(ii+1, jj)、A(ii+1, jj+1)等就能命中缓存(spatial locality)。
下面是各层cache miss的breakdown(外层的cache miss包含了内层的):
| loop/cache misses | A | B |
|---|---|---|
| jj | T | T/b |
| ii | T * T/b | T/b * T |
| J | T * T/b * N/T = NT/b | T/b * T * N/T = NT/b |
| I | NT/b * N/T = N*N/b | NT/b * N/T = N*N/b |
总结
循环分块的本质是在外层循环挖掘内层的temporal和spatial reuse。基本的方法是strip-mine-and-interchange。以下是takeaway:
- 循环分块是什么?如何做?
- 对于不同的循环层分块有什么不同的结果?
- 如何计算cache miss?
想了解更复杂的循环如何做tiling(譬如经典的矩阵乘法)以及tiling的合法性请看本系列第二讲:
https://zhuanlan.zhihu.com/p/301905385zhuanlan.zhihu.com

:内存)


,考试不担心...)













