皮尔逊相关系数

1. 总体皮尔逊（Pearson）相关系数
   如果有 A:{A1,A2,⋯,An}A:\{A_1, A_2, \cdots, A_n\}A:{A1​,A2​,⋯,An​} 和 Y:{Y1,Y2,⋯,Yn}Y:\{Y_1, Y_2, \cdots, Y_n\}Y:{Y1​,Y2​,⋯,Yn​} 这两组数据，并且这两组数据都是总体数据。（即调查所有对象而得出的数据），那么可以求出总体均值为：$$E(X)=\frac{{\sum }_{i=1}^n{X}_i}{n},E(Y)=\frac{{\sum }_{i=1}^n{Y}_i}{n}$$ 同时，总体协方差也就可以表示为：$$Cov(X,Y)=\frac{{\sum }_{i=1}^n(X_i-E(X))(Y_i-E(Y))}{n}$$ 协方差可以理解为 $X$ 和 $Y$ 的变化方向是否相同。但是，协方差要受到量纲的影响，因此不适合作为比较。

   有了协方差以及总体均值，那么总体皮尔逊(Pearson)相关系数便可表示为：$$\rho =\frac{Cov(X,Y)}{\sigma }=\frac{{\sum }_{i=1}^n\frac{(X_i-E(X))}{{\sigma }_X}\frac{Y_i-E(Y)}{{\sigma }_Y}}{n}$$其中，${\sigma }_X$ 和 ${\sigma }_Y$ 表示 $X$ 和 $Y$ 的标准差，计算公式为：$${\sigma }_X=\sqrt{\frac{{\sum }_{i=1}^n(X_i-E(X){)}^2}{n}},{\sigma }_Y=\sqrt{\frac{{\sum }_{i=1}^n(Y_i-E(Y){)}^2}{n}}$$我们还可以得出，$|{\rho }_{XY}|\le 1$，$0\le \rho \le 1$ 时，表示 $X$ 和 $Y$ 之间成正相关关系，反之则成负相关关系。

2. 样本皮尔逊(Pearson)系数
   样本均值：$\bar{X}=\frac{{\sum }_{i=1}^n{X}_i}{n},\bar{Y}=\frac{{\sum }_{i=1}^n{Y}_i}{n}$
   样本协方差为：$Cov(X,Y)=\frac{{\sum }_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}$ （注意分母是 $n-1$ ， 而不是 $n$ ! !）
   样本皮尔逊(Pearson)相关系数：$r_{XY}=\frac{Cov(X,Y)}{S_X{S}_Y}$
   其中，$$S_X=\sqrt{\frac{{\sum }_{i=1}^n(X_i-\bar{X}{)}^2}{n-1}},\sqrt{\frac{{\sum }_{i=1}^n(Y_i-\bar{Y}{)}^2}{n-1}}$$ 同样，分母都是 $n-1$ 哦！！

3. 关于皮尔逊相关系数容易理解错误的点
   $\bullet$ 必须要在两个变量线性相关时，求出的相关系数才能说明这两个变量的相关性
   $\bullet$ 异常点对于线性相关系数的影响很大，不能一概而论
   $\bullet$ 相关系数为0，只能说明这两个变量不是线性相关的，但也有可能会有其他更为复杂的关系。

4. 使用皮尔逊相关系数之前需要：
   $\bullet$ 做出散点图确定这两个变量是否初步拥有线性相关关系
   不确定两个变量的关系，及时相关系数很大也无法判断。
   确定两个变量具有线性相关关系，计算皮尔逊(Pearson)相关系数时，可以直接在 $Matlab$ 中调用 $corrceof$ 函数来计算。

假设检验

假设检验一般有如下几个步骤：

1. 提出原假设 $H_0$ 以及备择假设 $H_1$ (两个假设互补)
2. 在原假设成立的条件下，利用要检验的量构造一个满足某一分布的统计量（分布一般有：标准正态分布、$t$ 分布、${\chi }^2$ 分布、$F$ 分布）
3. 根据这个统计量，将检验对象带入统计量，得到一个检验值。
4. 确定置信水平（99%, 95%, 90%，一般选取95%），根据置信水平确定临界值。
5. 由检验值和临界值的大小来判断假设是否能够显著接受。

下面来看一个例子

首先必须画出散点图确定是否有相关性哦！！！

经过 $Matlab$ 处理后可得的相关系数表为：

这是一个对称矩阵，矩阵中的数据表示行和列的相关系数。

1. 提出假设：
   $H_0$ ：$r$ = 0，$H_1$ ：$r$ ≠ 0
2. 提出满足分布的统计量
   可以构造统计量为：$$t=r\sqrt{\frac{n-2}{1-r^2}}$$可以证明 $t$ 时服从自由度为 $n-2$ 的 $t$ 分布。
3. 带入得检验值
   看第一行、第二列的值为：0.0580，样本数为730，因此 $t^{\ast }=0.0580\sqrt{\frac{730-2}{1-0.0580^2}}=1.5676$
4. 给定置信水平，确定临界值
   给定置信水平为 95%，根据 $t$ 分布表查阅对应的临界值
   
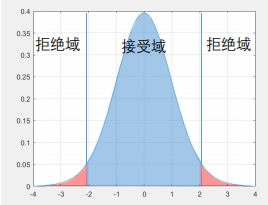
   比较检验值是否在接受域或者拒绝域。

$\{\begin{array}{rl}& \text{若在拒绝域，结论：在95\%的置信水平上，我们拒绝原假设，r显著不为0}\\ & \text{若在接受域，结论：在95\%的置信水平上，我们无法拒绝原假设}\end{array}$

5. 补充P值判断法
   根据得到的检验值 $t^{\ast }$，可以计算出这个检验值对应的概率。$$\{\begin{array}{rl}& \text{若是单侧检验，可在 Matlab 中}P=1-tcdf(t^{\ast },728)\\ & \text{若是双侧检验，可在 Matlab 中}P=(1-tcdf(t^{\ast },728))\times 2\end{array}$$

6. 皮尔逊相关系数假设检验的条件
   $\bullet$ 实验数据满足正态分布
   $\bullet$ 实验数据不能差距太大
   $\bullet$ 魅族样本之间时独立抽样的
   在平常的题目中，可以当作第二个和第三个条件成立。但是，第一个条件必须需要经过检验，检验成立才能使用皮尔逊(Pearson)相关系数检验。

7. 正态分布检验
   $\bullet$ 正态分布 $JB$ 检验（大样本 $n>30$ 时）

   对于一个随机变量{Xi}\{X_i\}{Xi​} ，假设其偏度为 $S$，峰度为 $K$，那么可以构造JB统计量：$$JB=\frac{n}{6}[S^2+\frac{(K-3{)}^2}{4}]$$可以证明，如果 {Xi}\{X_i\}{Xi​} 是正态分布，那么在大样本情况下 $JB-{\chi }^2(2)$ (自由度为2的卡方分布)
   注：正态分布的偏度为 0，峰度为 3

   那么假设检验的步骤如下：
   $H_0$：该变量服从正态分布，$H_1$：该随机变量不服从正态分布。
   然后可以计算变量的偏度和峰度，得到检验值 $J{B}^{\ast }$ ，并计算出其相应的 $p$ 值。
   将 $p$ 值与 0.05 作比较，小于 0.05 则可拒绝原假设，否则不能拒绝原假设。
   可以在 $Matlab$ 中调用 $[h,p]=jbtest(column,\text{置信水平})$，$h$ 表示 $J{B}^{\ast }$ 的值，$p$ 表示对应的 $p$ 值。

   $\bullet$ 夏皮洛-威尔克(Shapiro-wilk)检验

   $H_0$：该随机变量服从正态分布，$H_1$：该随机变量不服从正态分布
   计算出威尔克统计量后，可以求出对应的 $p$ 值
   将 $p$ 值与 0.05 比较，如果小于 0.05 则可以拒绝原假设，否则不能拒绝原假设。
   计算威尔克统计量可以使用 $SPSS$ 工具。

   $\bullet$ $Q-Q\text{图}$

   直接在 $Matlab$ 中调用 $qqplot(column)$ 函数做出图像，如果 $QQ$ 图近似于一条直线，该随机变量满足正态分布。
   注意：作 $QQ$ 图要求数据量非常大，做出图像才会更加准确。

斯皮尔曼(spearman)相关系数

1. 一种定义
   $X$ 和 $Y$ 为两组数据，其斯皮尔曼相关系数定义为：$$r_s=1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n(n^2-1)}$$其中，$d_i$ 为 $X_i$ 和 $Y_i$ 之间的等级差（一个数的等级 = 将它的一列数按照从小到大排序后，这个数的位置）
   同样，$r_s$ 位于 -1 和 1 之间
   |X|Y|X的等级|Y的等级|等级差|等级差的平方|
   |–|--|–|--|–|--|
   |3|5|2|1|1|1|
   |8|10|5|4.5|0.5|0.25|
   |4|8|3|3|0|0|
   |7|10|4|4.5|-0.5|0.25|
   |2|6|1|2|-1|1|
   根据公式：$$r_s=1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n(n^2-1)}$$可得：$$r_s=1-\frac{6\times (1+0.25+0.25+1)}{5\times 24}=0.875$$
2. 另一种定义
   等级之间的皮尔逊相关系数

X	Y	X的等级	Y的等级	等级差	等级差的平方
3	5	2	1	1	1
8	10	5	4.5	0.5	0.25
4	8	3	3	0	0
7	10	4	4.5	-0.5	0.25
2	6	1	2	-1	1

rank_X = [2 5 3 4 1]
rank_Y = [1 4.5 3 4.5 2]
R = corrcoef(rank_X, rank_Y)

在 $Matlab$ 中，可以使用 $corr()$ 函数，$corr(ran{k}_X,ran{k}_Y{,}^{\prime }typ{e}^{\prime }{,}^{\prime }Spearma{n}^{\prime })$
（注意：$Matlab$ 中使用的是第二种计算方法）

$\bullet$ 小样本情况下($n<30$)，可以直接查表

$\bullet$ 大样本情况下，可以构造统计量为：$r_s\sqrt{n-1}$
$H_0$：$r_s=0$，$H_1$：$r_s\ne 0$
计算检验值 $z^{\ast }=r_s\sqrt{n-1}$，并求出对应的 $p$ 值与 0.05 比较。$$\{\begin{array}{rl}& \text{若是单侧检验}，P=1-normcdf(z^{\ast })\\ & \text{若是双侧检验}，P=(1-normcdf(z^{\ast }))\times 2\end{array}$$或者直接在 $Matlab$ 中：$[R,P]=corr(ran{k}_X,ran{k}_Y{,}^{\prime }typ{e}^{\prime }{,}^{\prime }Spearma{n}^{\prime })$

注意

1. 皮尔逊相关系数条件：连续数据、正态分布、线性关系。
   因此，要使用皮尔逊相关系数：
   首先要是连续数据
   然后画散点图初步确定线性关系
   接着还要进行正态分布检验
   最后才能使用。

   当这些条件满足时，也可以使用斯皮尔曼相关系数，但是效率没皮尔逊相关系数高。

2. 上述条件任意不满足，就用斯皮尔曼相关系数，不能使用皮尔逊相关系数。

3. 两个定序数据也可以使用斯皮尔曼相关系数，不能使用皮尔逊相关系数。

有什么好的建议，烦请告知hhh~~~