基于计数的方法,根据一个单词周围的单词的出现频数来表示该单词。需要生成所有单词的共现矩阵,再对这个矩阵进行 SVD,以获得密集向量,如果语料库处理的单词数量非常大,将需要大量的计算资源和时间。基于计数的方法使用整个语料库的统计数据(共现矩阵、PPMI),通过一次处理(SVD)获得单词的分布式表示。
基于推理的方法,使用神经网络,在 mini-batch 数据上进行学习,神经网络一次只需要看一部分学习数据(mini-batch),并反复更新权重。神经网络的学习可以使用多台机器、多 个 GPU 并行执行,从而加速整个学习过程。
如果需要向词汇表添加新词并更新单词的分布式表示,基于计数的方法需要从头开始计算,重新完成生成共现矩阵、进行 SVD 等一系列操作。基于推理的方法(word2vec)允许参数的增量学习。可以将之前学习到的权重作为下一次学习的初始值,在不损失之前学习到的经验的情况下,高效地更新单词的分布式表示。
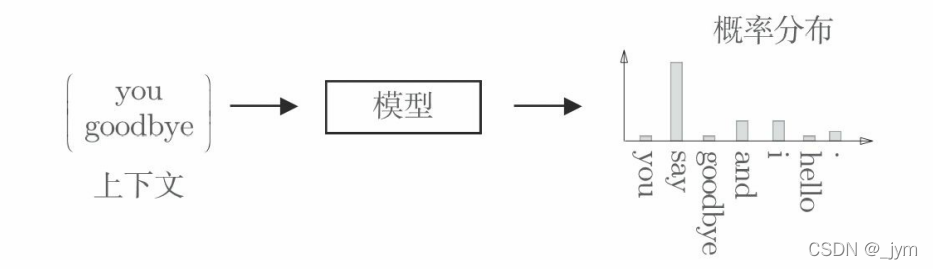
推理:当给出周围的单词(上下文)时,预测“?”处会出现什么单词。

基于推理的方法:输入上下文,模型输出各个单词的出现概率。这个模型接收上下文信息作为输入,并输出(可能出现的)各个单词的出现概率。作为模型学习的产物,也能得到单词的分布式表示。如下图所示。
分布式假设:基于推理的方法和基于计数的方法一样,也基于分布式假设。分布式假设,“单词含义由其周围的单词构成”。
one-hot 表示:神经网络无法直接处理 you 或 say 这样的单词,要用神经网络处理单词,需要先将单词转化为固定长度的向量。在 one-hot 表示中,只有一个元素是 1,其他元素都 是 0;将单词转化为 one-hot 表示,就需要准备元素个数与词汇个数相等的向量,并将单词 ID 对应的元素设为 1,其他元素设为 0。
单词的表示:单词可以表示为文本、单词 ID 和 one-hot 表示。如果语料库中,一共有 7 个单词(“you”“say”“goodbye”“and”“i”“hello”“.”),单词表示如下图所示。

将单词转化为固定长度的向量(one-hot 表示),神经网络的输入层的神经元个数就可以固定下来,比如,输入层由 7 个神经元表示,分别对应于 7 个单词。
全连接层变换:c 和 W 的矩阵乘积相当于“提取”权重的对应行向向量。
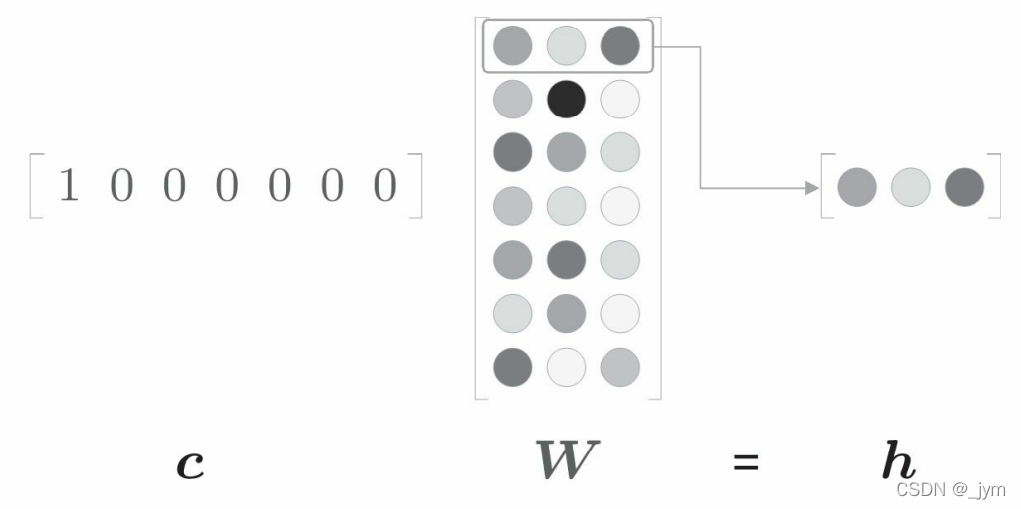
import numpy as np
c = np.array([[1, 0, 0, 0, 0, 0, 0]]) # 输入
W = np.random.randn(7, 3) # 权重
h = np.dot(c, W) # 中间节点
print(h)
# [[-0.70012195 0.25204755 -0.79774592]]
CBOW模型:它是根据上下文预测目标词的神经网络。模型的输入是上下文。这个上下文用 [‘you’, ‘goodbye’] 这 样的单词列表表示。可以转换为 one-hot 表示,以便 CBOW 模型进行处理。大致结构如下。
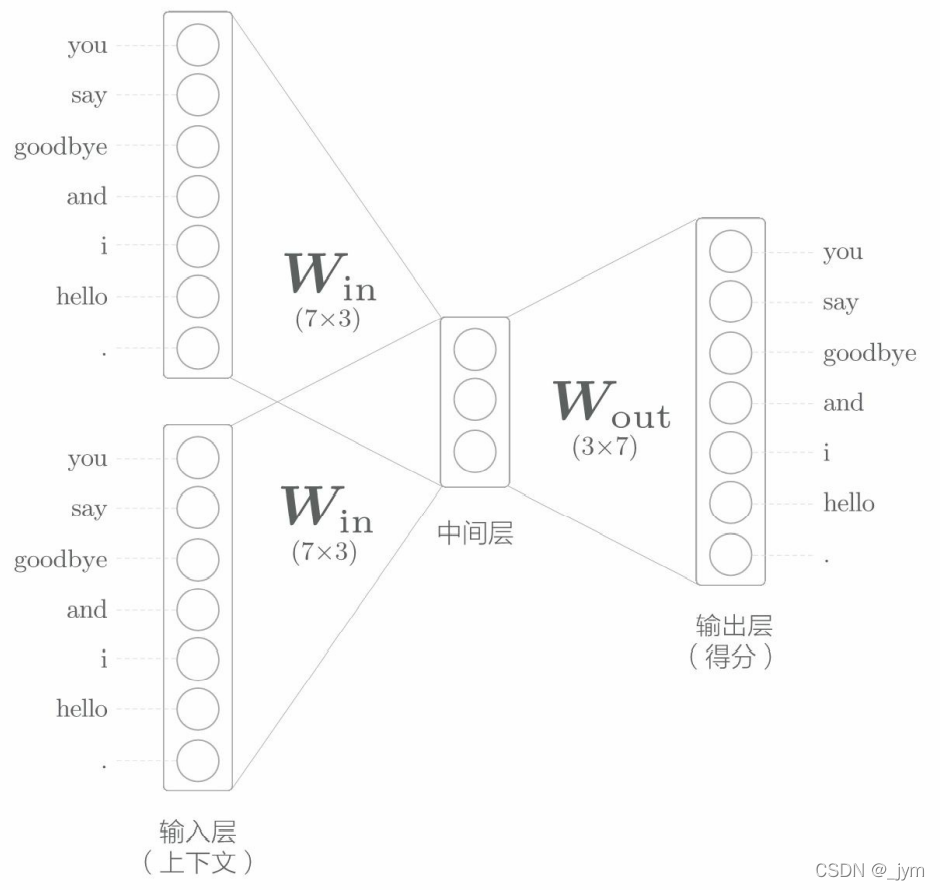
输入层:如果对上下文仅考虑两个单词,输入层有两个;如果对上下文考虑N个单词,则输入层会有N个。
中间层:中间层的神经元是各个输入层经全连接层变换后得到的值的平均,经全连接层变换后,第 1 个输入层转化为h1,第 2 个输入层转化为h2,那么中间层的神经元是(1/2)*(h1+h2)。中间层的神经元数量比输入层少,因为,中间层需要将预测单词所需的信息压缩保存,从而产生密集的向量表示。
输出层:输出层有 7 个神经元,这些神经元对应于各个单词。输出层的神经元是各个单词的得分,它的值越大,说明对应单词的出现概率就越高。对这些得分应用 Softmax 函数,就可以得到概率。
全连接层:从输入层到中间层的变换由全连接层完成,全连接层的权重是一个 7 × 3 的矩阵,权重的各行对应各个单词的分布式表示。



















