深入学习二叉树(三) 霍夫曼树

1 前言

霍夫曼树是二叉树的一种特殊形式，又称为最优二叉树，其主要作用在于数据压缩和编码长度的优化。

2 重要概念

2.1 路径和路径长度

在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

在这里插入图片描述
图2.1所示二叉树结点A到结点D的路径长度为2，结点A到达结点C的路径长度为1。

2.2 结点的权及带权路径长度

若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。
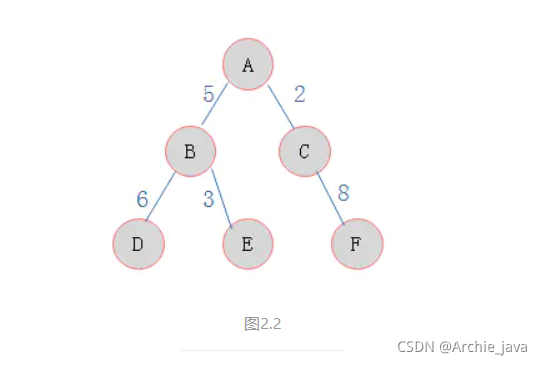
图2.2展示了一棵带权的二叉树

在这里插入图片描述

2.3 树的带权路径长度

树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。
图2.2所示二叉树的WPL：
WPL = 6 * 2 + 3 * 2 + 8 * 2 = 34；

3 霍夫曼树

3.1 定义

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为霍夫曼树(Huffman Tree)。
如图3.1所示两棵二叉树
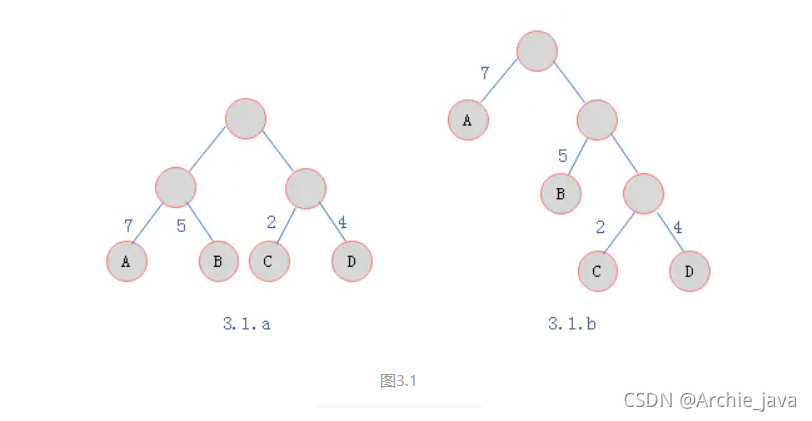
在这里插入图片描述
叶子结点为A、B、C、D，对应权值分别为7、5、2、4。
3.1.a树的WPL = 7 * 2 + 5 * 2 + 2 * 2 + 4 * 2 = 36
3.1.b树的WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3 = 35
由ABCD构成叶子结点的二叉树形态有许多种，但是WPL最小的树只有3.1.b所示的形态。则3.1.b树为一棵霍夫曼树。

3.2 构造霍夫曼树

构造霍夫曼树主要运用于编码，称为霍夫曼编码。现考虑使用3.1中ABCD结点以及对应的权值构成如下长度编码。
AACBCAADDBBADDAABB。
编码规则:从根节点出发，向左标记为0，向右标记为1。
采用上述编码规则，将图3.1编码为图3.2所示：

在这里插入图片描述
构造过程：
3.1.a所示二叉树称为等长编码，由于共有4个结点，故需要2位编码来表示，编码结果为：

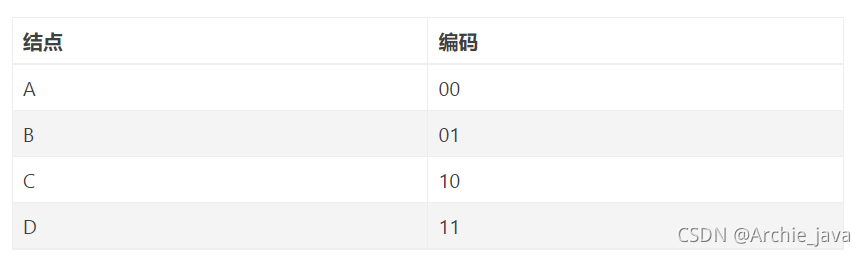
则AACBCAADDBBADDAABB对应编码为：
00 00 10 01 10 00 00 11 11 01 01 00 11 11 00 00 01 01
长度为36。
3.1.b构造过程如下：
1）选择结点权值最小的两个结点构成一棵二叉树如图3.3：

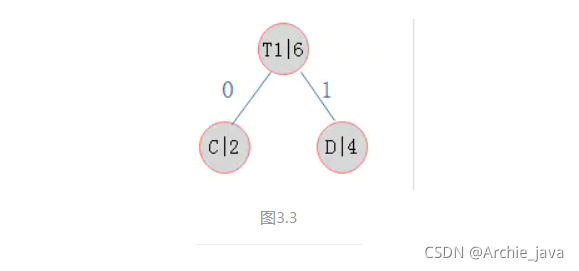
在这里插入图片描述
2）则现在可以看作由T1，A，B构造霍夫曼树，继续执行步骤1。
选则B和T1构成一棵二叉树如图3.4：

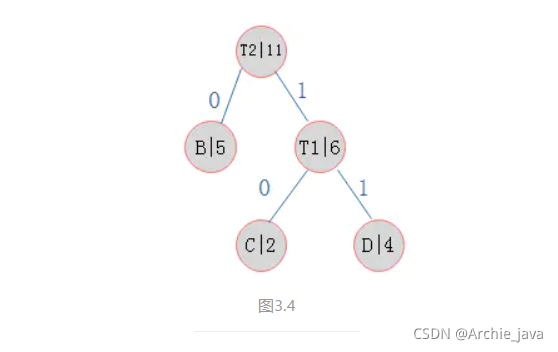
在这里插入图片描述
3）现只有T2和A两个结点，继续执行步骤1。
选择A和T2构成一棵二叉树如图3.5：

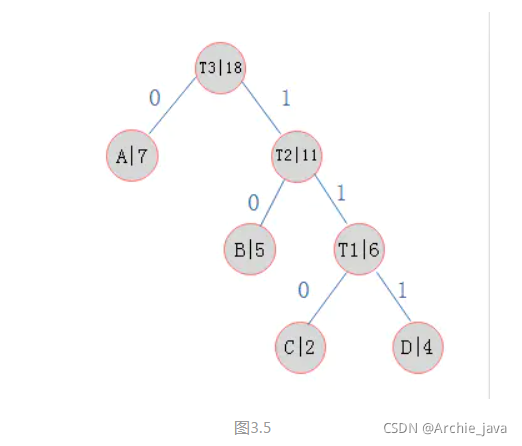
经过上述步骤则可以构造完一棵霍夫曼树。通过观察可以发现，霍夫曼树中权值越大的结点距离根结点越近。
按照图3.5霍夫曼树编码结果：
在这里插入图片描述
则AACBCAADDBBADDAABB对应编码为：
0 0 110 10 110 0 0 111 111 10 10 0 111 111 0 0 10 10
编码长度为35。
由此可见，采用二叉树可以适当降低编码长度，尤其是在编码长度较长，且权值分布不均匀时，采用霍夫曼编码可以大大缩短编码长度。

3.3 代码实现

#include <iostream>
#include <stdlib.h>
using namespace std;
const int MaxValue = 10000;//初始设定的权值最大值
const int MaxBit = 4;//初始设定的最大编码位数
const int MaxN = 10;//初始设定的最大结点个数
struct HaffNode//哈夫曼树的结点结构
{int weight;//权值int flag;//标记int parent;//双亲结点下标int leftChild;//左孩子下标int rightChild;//右孩子下标
};
struct Code//存放哈夫曼编码的数据元素结构
{int bit[MaxBit];//数组int start;//编码的起始下标int weight;//字符的权值
};
void Haffman(int weight[], int n, HaffNode haffTree[])
//建立叶结点个数为n权值为weight的哈夫曼树haffTree
{int j, m1, m2, x1, x2;//哈夫曼树haffTree初始化。n个叶结点的哈夫曼树共有2n-1个结点for (int i = 0; i<2 * n - 1; i++){if (i<n)haffTree[i].weight = weight[i];elsehaffTree[i].weight = 0;//注意这里没打else那{}，故无论是n个叶子节点还是n-1个非叶子节点都会进行下面4步的初始化haffTree[i].parent = 0;haffTree[i].flag = 0;haffTree[i].leftChild = -1;haffTree[i].rightChild = -1;}//构造哈夫曼树haffTree的n-1个非叶结点for (int i = 0; i<n - 1; i++){m1 = m2 = MaxValue;//Maxvalue=10000;(就是一个相当大的数)x1 = x2 = 0;//x1、x2是用来保存最小的两个值在数组对应的下标for (j = 0; j<n + i; j++)//循环找出所有权重中，最小的二个值--morgan{if (haffTree[j].weight<m1&&haffTree[j].flag == 0){m2 = m1;x2 = x1;m1 = haffTree[j].weight;x1 = j;}else if(haffTree[j].weight<m2&&haffTree[j].flag == 0){m2 = haffTree[j].weight;x2 = j;}}//将找出的两棵权值最小的子树合并为一棵子树haffTree[x1].parent = n + i;haffTree[x2].parent = n + i;haffTree[x1].flag = 1;haffTree[x2].flag = 1;haffTree[n + i].weight = haffTree[x1].weight + haffTree[x2].weight;haffTree[n + i].leftChild = x1;haffTree[n + i].rightChild = x2;}
}
void HaffmanCode(HaffNode haffTree[], int n, Code haffCode[])
//由n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
{Code *cd = new Code;int child, parent;//求n个叶结点的哈夫曼编码for (int i = 0; i<n; i++){//cd->start=n-1;//不等长编码的最后一位为n-1,cd->start = 0;//,----修改从0开始计数--morgancd->weight = haffTree[i].weight;//取得编码对应权值的字符child = i;parent = haffTree[child].parent;//由叶结点向上直到根结点while (parent != 0){if (haffTree[parent].leftChild == child)cd->bit[cd->start] = 0;//左孩子结点编码0elsecd->bit[cd->start] = 1;//右孩子结点编码1//cd->start--;cd->start++;//改成编码自增--morganchild = parent;parent = haffTree[child].parent;}//保存叶结点的编码和不等长编码的起始位//for(intj=cd->start+1;j<n;j++)for (int j = cd->start - 1; j >= 0; j--)//重新修改编码，从根节点开始计数--morganhaffCode[i].bit[cd->start - j - 1] = cd->bit[j];haffCode[i].start = cd->start;haffCode[i].weight = cd->weight;//保存编码对应的权值}
}
int main()
{int i, j, n = 4, m = 0;int weight[] = { 2,4,5,7 };HaffNode*myHaffTree = new HaffNode[2 * n - 1];Code*myHaffCode = new Code[n];if (n>MaxN){cout << "定义的n越界，修改MaxN!" << endl;exit(0);}Haffman(weight, n, myHaffTree);HaffmanCode(myHaffTree, n, myHaffCode);//输出每个叶结点的哈夫曼编码for (i = 0; i<n; i++){cout << "Weight=" << myHaffCode[i].weight << "  Code=";//for(j=myHaffCode[i].start+1;j<n;j++)for (j = 0; j<myHaffCode[i].start; j++)cout << myHaffCode[i].bit[j];m = m + myHaffCode[i].weight*myHaffCode[i].start;cout << endl;}cout << "huffman's WPL is:";cout << m;cout << endl;return 0;
}