第三十五集 中心极限定律
　　该定律是说随着样本n越来越大，这n个样本的m个均值会趋于正态分布。与大数定律的区别在于：大数定律描述的样本均值趋于总体均值，而中心极限定律描述的是样本均值的分布。

第三十六、七集 样本均值的抽样分布
　　样本均值抽样分布是所有样本均值抽样形成的分布。其中偏度与峰度是描述一个分布有多像正态分布的物理量。其中正偏度表示数据正向的多，负偏度表示数据负向的多。峰度反映了锋部的尖度。

第三十八、九集 均值标准误差
　　样本均值抽样分布是所有样本均值抽样形成的分布。均值标准差是样本均值抽样分布的标准差，其和总体标准差的关系为：

第四十、三、四集 置信区间与误差估计
　在样本估计总体均值时，我们需要知道估计的准确度，因此选定一个区间[a,b]，目的是让这个区间包含总体均值，这个区间叫做置信区间。对于这个区间有多大概率包含总体均值，这个概率称为置信水平。置信水平是根据实际问题自己确定的，一般设定为95%即两个标准差。总之：置信区间是我们计算变量的存在范围，置信水平是我们对这个范围的可信程度。

置信区间计算方法：首先，计算样本均值，样本均值标准差为。这几个公式的问题是事先我们并不知道总体的标准差。因此我们需要用估计值来代替。我们选择样本方差作为总体方差的估计，需注意是会跟随样本的变化而变化的，如图2所示。其次确定置信水平，最后查找z表格，计算置信区间。
　　

第四十一、二集 伯努利分布
　　二项分布是n重伯努利实验成功次数的分布，个人认为放在二项分布之前讲解更好。伯努利分布又叫两点分布或者0-1分布。

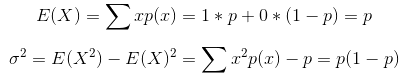
第四十六集 小样本容量置信区间
　　当样本数量小于30时，样本分布不再符合正态分布而是符合T分布。T分布只有一个自由度参数n，当n趋于无穷时，T分布变为标准正态分布，其实T分布只是正态分布的一种近似，是正态分布在小样本时的形态。计算置信区间的方法和正态分布类似，不同的是要查t分布表而不是z分布表。