假设检验

假设检验是推论统计中用于检验统计假设的一种方法。而“统计假设”是可通过观察一组随机变量的模型进行检验的科学假说。一旦能估计未知参数，就会希望根据结果对未知的真正参数值做出适当的推论。统计上对参数的假设，就是对一个或多个参数的论述。而其中欲检验其正确性的为零假设（null hypothesis），零假设通常由研究者决定，反映研究者对未知参数的看法。相对于零假设的其他有关参数之论述是备择假设（alternative hypothesis），它通常反映了执行检定的研究者对参数可能数值的另一种（对立的）看法（换句话说，备择假设通常才是研究者最想知道的）。假设检验的种类包括：t检验，z检验，卡方检验，F检验等等。

（百度百科）

在假设检验的问题中，通常需要根据已有的统计量对某一个假设进行检验。我们得到的统计量通常是样本均值的抽样分布，服从正态分布（当n足够大时，例如n>=30）或t分布（当n<30)。在零假设成立的条件下，计算出现样本统计量的概率。如果概率值小于某个阈值，则“拒绝”零假设，接受备择假设。在这个问题中，有两个假设的概念：

零假设，通常记为 $H_0$ 。备择假设，通常记为 $H_1$ 或 $H_a$ 。

假设检验通常检验零假设的正确性，也即是问题中的假设的对立假设，对于利用这个零假设进行检验，我理解的原因是：题目中真正需要进行检验的假设通常不能提供确切的统计数值用于计算，而零假设可以充分利用题目中所给的条件，利用反正法推翻零假设，就证明了备择假设的可信性。

p-value：在零假设成立的条件下，出现样本统计情况的概率通常很小，将这种极端情况的概率值称为p-value，通常设置5%为门限，当p-value低于这个门限时，就拒绝零假设。

双侧检验（two-tailed test）：当样本出现的极端情况可能出现在总体分布的两侧尾部时，称为双侧检验。通常题目中的假设要求检验某个统计量是否变化；

单侧检验（one-tailed test）：当样本出现的极端情况只可能出现在总体分布的一侧尾部时，只需检测一侧的尾部，称为单侧检验。通常题目中的假设要求检验某个统计量向某个方向的变化。

z-统计量和 t-统计量

与样本容量有关。当样本容量很大时（n>=30），样本统计量（不一定是均值，可能是其他计算量）的抽样分布服从正态分布，此时计算概率时使用z分布的计算表；当样本容量不是很大（n<30）时，样本统计量的抽样分布不再服从正态分布，而服从t分布，此时使用t分布的计算表。

第一型错误（type 1 error）：拒绝了正确的零假设的概率，也就是零假设判断错误的概率。

大样本占比的假设检：

样本占比实验可以理解为伯努利实验，占比就是伯努利实验的成功率。n次伯努利实验是二项分布，当n很大时，二项分布趋近于正态分布。具体地，当np>5,且n(1-p)>5,则可以假定样本占比的分布为正态分布。

随机变量之差的方差：

$\mu _{X+Y}=\mu _X+\mu _Y$

$\mu _{X-Y}=\mu _X-\mu _Y$

$\sigma _{X+Y}=\sigma _X+\sigma_Y$

$\sigma _{X-Y}=\sigma_X+\sigma _Y$

1.线性回归

统计学中的线性回归：对于一组具有线性关系的数据，可以用一条直线来拟合这些数据。用于拟合这些数据的直线应该使得所有数据到这条直线的距离最短（这里的距离简化为真实值和预测值之间的距离）。

设这条直线为：y=mx+b

其中，m为直线的斜率，b为截距。线性回归学习的目的是找到这样的参数m和b，使得所有数据点到这条直线的距离最短。数据点到直线的距离的平方之和，或说是平方误差为：

$\begin{aligned} SE_{Line}=&\sum_{i=1}^{n}(y_i-mx_i-b)^2\\ =&\sum_{i=1}^{n}y_i^2-2(mx_i+b)y_i+(mx_i+b)^2\\ =&\sum_{i=1}^{n}y_i^2-2mx_iy_i-2by_i+m^2x_i^2+b^2+2mbx_i\\ =&n\bar{Y^2}-2mn\bar{XY}-2bn\bar{Y}+m^2n\bar{X^2}+nb^2+2mnb\bar{X} \end{aligned}$

分别对m和b求偏导，并令其为0，可得：

$\frac{\partial SE_{Line}}{\partial m}=-2n\bar{XY}+2mn\bar{X^2}+2nb\bar{X}=0$

$\frac{\partial SE_{Line}}{\partial b}=-2n\bar{Y}+2nb+2mn\bar{X}=0$

求得：

$m=\frac{\bar{XY}-\bar{X}\bar{Y}}{\bar{X^2}-(\bar{X})^2}$

$b=y-mx$

决定系数(coefficient of determination)： y的波动多大程度上可以被x的波动描述,what % of the total variation is described by the variation in x

$r^2=1-\frac{SE_{Line}}{SE_{\bar{Y}}}$

其中:

$SE_{Line}=\sum_{i=1}^{n}(y_i-(mx_i+b))^2$ ,

$SE_{\bar{Y}}=\sum_{i=1}^{n}(y_i-\bar{y})^2$

当 $SE_{Line}$ 很小时，说明直线很好地拟合了数据 $\rightarrow$ $\frac{SE_{Line}}{SE_{\bar{Y}}}$ 很小 $\rightarrow$ $r^2$ 接近于1；当 $SE_{Line}$ 的值较大时，说明直线不能很好地拟合数据 $\rightarrow$ $\frac{SE_{Line}}{SE_{\bar{Y}}}$ 接近1 $\rightarrow$ $r^2$ 接近于0。因此从 $r^2$ 的值可以推断出直线的拟合程度。

线性回归的斜率与随机变量协方差的关系：

令X,Y为两个随机变量，X和Y的协方差定义为：

$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]$

可以化简为：

$\begin{aligned} Cov(X,Y)=&E[(X-E[X])(Y-E[Y])]\\ =&E[XY-XE[Y]-E[X]Y+E[X]E[Y]]\\ =&E[XY]-E[X]E[Y]-E[X]E[Y]+E[X]E[Y]\\ =&E[XY]-E[X]E[Y] \end{aligned}$

当X=Y时，有 $Cov(X,X)=E[(X-E[X])(X-E[X])]=Var[X]$ ,即X和X的协方差等于X的方差

上式中的期望可以用样本均值来估计，即：

$E[XY]\approx \bar{XY}$ , $E[X]\approx \bar{X}$ , $E[Y]\approx \bar{Y}$

则用样本均值估计的协方差可以写为： $Cov(X,Y)\approx \bar{XY}-\bar{X}\bar{Y}$

这是不是有点熟悉？线性回归拟合的直线中的斜率就有上述类似的表达式。随机变量的协方差是总体的统计量，而样本均值是对样本的统计量。之前得到的回归线的斜率可以看成是从总体分布中抽样得到的一个值，可以表示为：

$\hat{m}=\frac{\bar{XY}-\bar{X}\bar{Y}}{\bar{X^2}-(\bar{X})^2}$

则关于总体的回归线斜率为：

$m=\frac{Cov(X,Y)}{Var(X)}$

$\chi ^2$ 分布（Chi-Squared distribution）

假设有一些相互独立的服从标准正态分布的变量，例如： $X_1,X_2,\cdots$ ,另外一些变量与它们的关系为：

$\begin{aligned} Q_1=&X^2\\ Q_2=&X_1^2+X_2^2\\ Q_3=&X_1^2+X_2^2+X_3^2 \end{aligned}$

则称 $Q_1,Q_2,Q_3$ 分别服从分布： $Q_1\sim \chi ^2_1,Q_2\sim\chi^2_2,Q_3\sim\chi^2_3$ 。下标1，2，3分别表示自由度为1，2，3。

$\chi ^2$ 检验(待补充)

皮尔逊 $\chi ^2$ 检验

列联表（contingency table） $\chi ^2$ 检验

列联表自由度： $n=(c-1)(r-1)$

自由度是真正独立的数据点个数

2.方差分析

总平均值（grand mean) ,所有样本的均值，记为 $\mu$

总平方和（sum square total）SST，所有样本离总平均值的距离的平方和。

$SST=\sum_{i=1}^{N}(x_i-\mu)^2$ ，自由度为mn-1

组内平方和（the sum of squares within）SSW，每一组的样本离本组的均值的距离的平方和的和。设每组均值分别为 $\mu_1,\mu_2,\mu_3$ :

$SSW=\sum_{j=1}^{m}\sum_{i=1,x_i\in g_j}^{n}(x_i-\mu_j)^2$ ，自由度为m（n-1）

组间平方和（sum of squares between）SSB，每个样本点所在组的均值与总体均值的距离的平方和。

$SSB=\sum_{j=1}^{m}n(\mu_j-\mu)^2$ ,自由度为m-1

重要结论：总体波动可以描述为组内波动与组间波动的和。SST=SSW+SSB

总体的自由度=组内自由度+组间自由度。

第七十一集协方差
度量各个维度偏离其均值的程度。协方差是为多维变量创立的，目的是为了描述两个变量的关系（正相关，负向关。相互独立）。需注意协方差只能两个维度算，多个维度的协方差形成协方差矩阵。
cov(X,Y)=E[(x-E[X])(y-E[Y])]
在这里插入图片描述
第七十二集卡方分布
一些服从标准正态随机变量的平方求和即是分布，其中n为自由度，确定一个式子自由度的方法是：
若式子包含有n个独立的随机变量,和由它们所构成的k个样本统计量,则这个表达式的自由度为n-k.比如中包含ξ1,ξ2,…,ξn这n个独立的随机变量,
同时还有它们的平均数ξ这一统计量,因此自由度为n-1.。
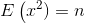
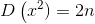
在这里插入图片描述

第七十三、四集卡方检验
　　卡方分布可以不用对总体做任何假设，卡方检验可以用来衡量观测与理论之间的拟合程度，或者推断两个分类变量是否相关或者独立。

具体例子可参考:https://blog.csdn.net/bitcarmanlee/article/details/52279907
第七十五、六集平方和
组内平方和：是每组的值减去每组自己的平均值，求平方和，组间平方和理解为两组之间的差异。

组间平方和：是每组自己的平均值减去总均值，求平方和，组内平方和理解为两组内部不同数据的差异。

如图：这几集的内容是为了说明总的波动=组内波动+组间波动
在这里插入图片描述
F假设检验
　　F统计量是组间平方和除以其自由度比上组内平方和除以其自由度。F值主要描述：组间的差异大，还是组内的差异大？如果是组间的差异大，那么这两组数据本身不一致的概率就大，对应F值比较大。F检验又称为方差其次性检验，检查的是方差的差异性。需注意：F检验的前提是F分布，而F分布的前提是正态分布。F检验通常作为T检验的一步。
　　在这里插入图片描述各个分布的应用如下：
方差已知情况下求均值是Z检验。
方差未知求均值是t检验（样本标准差s代替总体标准差R，由样本平均数推断总体平均数）
均值方差都未知求方差是X^2检验
两个正态分布样本的均值方差都未知情况下求两个总体的方差比值是F检验。