文章目录
- 函数指针简介
- 格式介绍
- 颜色头文件
- 计算机仿真
- 使用说明
- 完整代码
- 部分效果图
函数指针简介
如果在一个大型C语言程序中要反复调用函数,而调用的函数又不明确时,函数指针就是一个非常有用的东西。如果你的函数体内可以传递不同的函数,那就非得用函数指针实现不可。下面我就用一个例子给大家分享一下C语言函数指针的妙用。
格式介绍
格式为:【基类型】(*function)([参数表列])
C语言函数指针就是一个指向函数地址的指针,它和普通的指针一样也具有基类型,例如int *p,double *q,void *malloc与普通指针不同的是,它指向的不是特定类型的变量,而是函数地址,因此它后面有函数的参数表列。使用的时候需要注意,由于指针运算符比括号运算符的优先级低,因此需要把(*function)括起来(否则就是返回指针的函数)。C语言的语法比较复杂,举一个函数指针的例子:
#include <stdio.h>
#include <stdbool.h>
int max(int a,int b);//最大值函数
int min(int a,int b);//最小值函数
int main()
{int a,b;int (*p)(int,int);//函数指针pbool choice;char c[4];//字符串printf("Please enter two integer(separate by space): ");scanf("%d%d",&a,&b); printf("Please choose a function(0: max,1: min): ");scanf("%d%d",&choice);if(choice){p=min;c="min"}else {p=max;c="max"};//让函数指针指向选择的函数(地址)printf("%s=%d",c,p(a,b));//完成选择函数的输出return 0;
}
函数指针主要有两种使用方法:
- 用函数指针指向某个函数做选择(类似于上述的例子)
- 当做函数的参数传递(类似于下面的代码),使程序模块化更强,耦合性更弱当做函数的参数传递,使程序模块化更强,耦合性更弱
下面是我编写的一个计算一个指定方波的程序,里面的双线性积分函数对每一次谐波变量(int n)都一个返回谐波分量double amplify,在这里用到了函数指针,传递一个方波的函数给这个积分函数,如果以后这个函数不是方波而是其他函数,增添和修改代码都会非常方便!
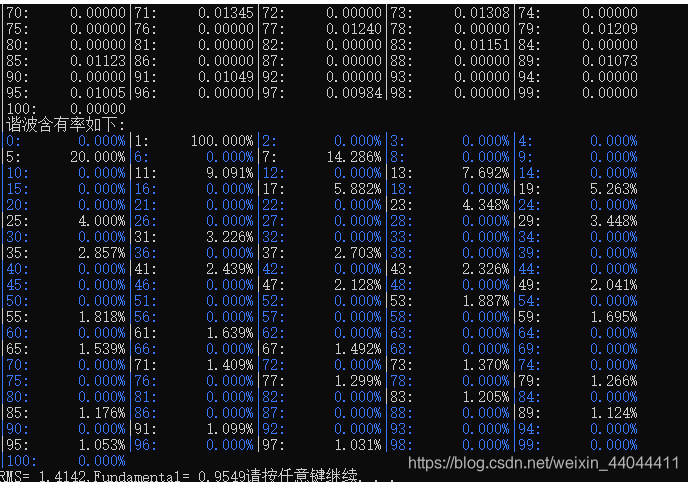
在程序里面我指定的值是电力电子课程里面的三相全桥整流电路带阻感性负载的变压器二次侧电流波形的方波(一周期脉动6次的交流电平),方波应该没有2次和3次谐波,这样只剩下了1次谐波和6k±1(k∈N*)次谐波,每次谐波含有率(和1次谐波的比值)为1/(6k±1),可以看到后面附图里面确实非常准确,1,0.2,0.14286,…分别是1,1/5,1/7,…!
如果我们分析三相电压型桥式逆变电路的Unn’中点电压波形(一周期脉动6次的交流方波信号),可以得出同样的结果。为了让输出的谐波分析更加的美观,我们让谐波含有率低于1e-4的所有的次谐波都标蓝,剩下的白色的才是真正含有的谐波,供我们进行计算机仿真实验验证。
颜色头文件
以下链接为C语言彩色打印字符的相关头文件及其说明:
【博客链接】
计算机仿真
使用说明
在程序的开始界面输入时刻表和对应的电平表,输入分析基频以及最高的分析谐波次数,程序即可进入运算状态。由于使用的是CFT(连续傅里叶积分),可能计算会有点慢,大概3秒算10次谐波。如果谐波含有率很低会用蓝色标识出来,其余的谐波用白色标注,代表实质有的谐波含量,方便大家发现规律。输入时刻表列和电平表列的规则如下:
如果一个方波的电平以-1和1两个电平变化,并且周期为π,则输入周期为π,改变电平的时刻表列为0(不包括2个端点),电平表列为-1 1.
如果一个方波的电平以-1,0,1,0,-1,0,…变化,正负电平的持续时间是0电平的2倍,周期为π,则电平的时刻表列为-5π/12,-π/12,π/12,5π/12(不包括2个端点),电平表列为0 -1 0 1 0。
由于输入的时刻表列不包括两个端点,因此时刻表列总是比电平表列多一个数值,但是如果时刻表列加上2个端点时刻,正好形成和电平表列数目一样多的时间段和电平表列相对应。输入规则就是这样的。
完整代码
//#include <stdio.h> //color.h已包括
#include <math.h>
#include <ctype.h>
#include <malloc.h>
//#include <windows.h> //color.h已包括
#include "color.h"
#define pi 3.14159265
double amplify(double (*function)(double x),int n);//双线性积分函数,参数为函数指针、上界、下界
double RMS(double (*function)(double x));//对一个函数在周期内求有效值
double square_wave(double x);
double period;//被分析方波的周期
double time[30]={0};//方波的时间时刻数组,首地址是从0附近的周期最左边的坐标开始的依次改变的电平处的值,只保留一个周期的
double level[30]={0};//方波的电平数组,表示与时间区别对应的电平
int fund_f;//指定傅里叶分解时的基频
int count=0;//统计输入个数
//以上为声明
int main()
{char t;//用于检测字符是否数字,实现动态输入 int i=0;//扫描计数偏移量int Nc;//截止谐波次数 double *AP=NULL;//用于存放幅值数组的指针 //以上为定义变量部分 printf("***对用户定义的方波进行傅里叶级数展开***\n请输入方波的周期: ");scanf("%lf",&period);fflush(stdin);printf("请输入方波的在(-T/2,T/2)周期改变电平的时间时刻(不含±T/2的时刻,用空格分隔):\n");while((t=getchar())!='\n'){if(isdigit(t)||t=='-')//浮点数都是以负号或者数字开头的 {ungetc(t,stdin);scanf("%lf",time+i);//扫描的浮点数一次存入 count++;//统计输入时间节点的个数 i++; }} *(time+i+1)=period/2;printf("请输入方波的在上述改变时间时刻对应的电平值\n【说明】第一个电平对应(-T/2,t0),最后一个电平对应(tn,T/2),用空格分隔:\n");fflush(stdin);//循环结束,刷新标准输入口 i=0;//偏移量清零 while((t=getchar())!='\n'){if(isdigit(t)||t=='-')//浮点数都是以负号或者数字开头的 {ungetc(t,stdin);scanf("%lf",level+i);//扫描的浮点数一次存入 i++;}} fflush(stdin);//循环结束,刷新标准输入口 printf("请输入傅里叶分解的基频: ");scanf("%d",&fund_f);printf("请输入分析的谐波最高次数: ");scanf("%d",&Nc);AP=(double *)calloc(Nc,sizeof(double));if(AP==NULL){printf("\n\r意外错误:内存分配失败!\n");return 1;}printf("\n\r动态内存分配成功!\n");for(i=0;i<=Nc;i++){AP[i]=amplify(square_wave,i);printf("\r正在计算中...%.2lf%%",100*(float)i/Nc);}printf("\n\r|谐波次数:\t振幅\n");for(i=0;i<=Nc;i++){printf("|%d:\t%8.5lf",i,AP[i]);if((i+1)%5==0)printf("\n");}printf("\n\r|谐波含有率如下:\n");for(i=0;i<=Nc;i++){if(AP[i]/AP[1]<1e-4){setcolor(LIGHTBLUE);//无该次谐波的显示为黄色 printf("|%d:\t%7.3lf%%",i,100*AP[i]/AP[1]);}else{setcolor(WHITE);//有该次谐波显示为蓝色 printf("|%d:\t%7.3lf%%",i,100*AP[i]/AP[1]); } if((i+1)%5==0)printf("\n");}setcolor(WHITE);//还原默认色 printf("\n\rRMS=%7.4lf,Fundamental=%7.4lf",RMS(square_wave),AP[1]);system("pause");return 0;
}
//根据电平数组和时间间隔数组查找对应时间的方波的电平
double square_wave(double x)
{int i;for(i=0;i<count;i++){if(x<*(time+i))return *(level+i);}return *(level+count);//如果均不是,返回level数组的最后一个值,即[tn,T/2]的值
}
double amplify(double (*function)(double x),int n)
{double sin_integral=0,cos_integral=0;//积分值double x0,x1;//双线性积分需要两个变量迭代计算for(x1=-period/2;x1<period/2;x0=x1,x1+=1e-5){sin_integral+=0.5*1e-5*((*function)(x1)*sin(n*2*pi*fund_f*x1/period)+(*function)(x0)*sin(n*2*pi*fund_f*x0/period));cos_integral+=0.5*1e-5*((*function)(x1)*cos(n*2*pi*fund_f*x1/period)+(*function)(x0)*cos(n*2*pi*fund_f*x0/period));} return sqrt(pow(sin_integral,2)+pow(cos_integral,2))/period;
}
double RMS(double (*function)(double x))
{double integral=0;double x0,x1;//采用双线性积分for(x1=-period/2;x1<period/2;x0=x1,x1+=1e-5){integral+=0.5*1e-5*(pow((*function)(x1),2)+pow((*function)(x0),2)); }return sqrt(integral/period);
} 部分效果图
希望本文对您有帮助,谢谢阅读。




为例展示)















