java 逻辑表达式 布尔

将布尔表达式转换为逻辑电路 (Converting Boolean Expression to Logic Circuit)

The simplest way to convert a Boolean expression into a logical circuit is to follow the reverse approach in which we start from the output of the Boolean expression and reach towards the input.

将布尔表达式转换为逻辑电路的最简单方法是遵循相反的方法，在这种方法中，我们从布尔表达式的输出开始，然后向输入过渡。

Example1: Realize the Boolean Expression BC + A + (A + C) using AOI logic.

示例1：使用AOI逻辑实现布尔表达式BC + A + (A + C) 。

Solution:

解：

To realize this using the AOI logic gates, we will use the reverse approach.

为了使用AOI逻辑门来实现这一点，我们将使用相反的方法。

Step 1:

第1步：

Our expression BC + A + (A+C) is the summation of three terms BC, A and, (A+C), thus a 3-input OR Gate must have been used to obtain the expression as given :0

我们的表达BC + A +(A + C)是三个方面BC，A和(A + C)的总和，从而一个3输入OR门必须被用于获得表达给出：0

Step 2:

第2步：

Now, BC and (A + C) both are inverted in nature, so they must have been inverted using a NOT Gate earlier. BC must have been obtained by inverting the input BC and (A + C) must have been obtained by inverting the input (A + C) both using the NOT Gate.

现在， BC和(A + C)本质上都是反向的，因此它们必须早先使用NOT门进行了反向。 BC必须已经通过反相输入BC获得，并且(A + C)必须已经通过使用NOT门将输入(A + C)反相获得。

Step 3:

第三步：

Moving further, in the reverse direction we see, BC must have been an output of 2-input AND Gate with inputs as B and C. Likewise, (A + C) must have been obtained as the output of 2-input OR gate with A and C as the inputs.

再往相反方向看，BC必须是输入为B和C的2输入与门的输出。同样，必须获得(A + C)作为2输入与门的输出，其中A和C作为输入。

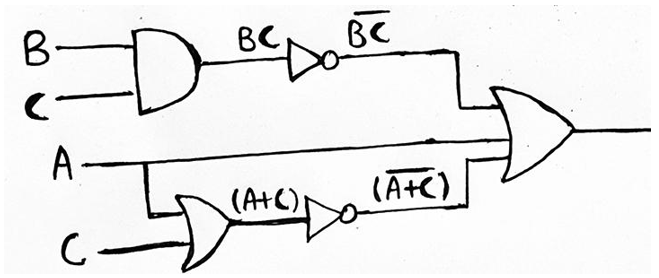
So, Final Logic Diagram for above given Boolean expression can be drawn as,

因此，以上给出的布尔表达式的最终逻辑图可以绘制为：

将逻辑图转换为布尔表达式 (Converting Logic Diagrams into Boolean Expressions)

The easiest way to obtain the Boolean Expression from any logic circuit is to follow the forward propagation approach. In this, we start from the input side and move ahead until the output is reached. While moving from the input side to the output side, we continue evaluating the output of intermediate logic gates.

从任何逻辑电路获得布尔表达式的最简单方法是遵循正向传播方法。 在这种情况下，我们从输入端开始，然后继续前进，直到达到输出为止。 从输入端移至输出端时，我们继续评估中间逻辑门的输出。

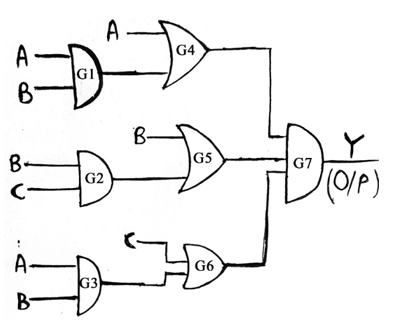
Example 1: Find out the Boolean Expression for Logic Diagram given below and simplify the output in the minimal expression, also implement the simplified expression using the AOI logic.

示例1：找出下面给出的逻辑图布尔表达式，并以最小表达式简化输出，还使用AOI逻辑实现简化表达式。

Solution:

解：

Following the forward propagation approach, we see that gate G1 is a 2-input AND Gate having inputs A and B. So, output of G1 will be AB. Similarly, G2 is an OR Gate, so output of G2 will be (B+C). Also, G3 is an AND Gate and its output will be AB.

按照前向传播方法，我们看到门G1是2输入与门，其输入A和B。因此，G1的输出将为AB。 同样，G2是“或”门，因此G2的输出为(B + C)。 同样，G3是与门，其输出将为AB。

Now, gate G4 is a 2-input OR Gate which has one of its inputs as A and the other one is the output of gate G1, thus the output of gate G4 will be (A + AB). Similarly, output for gate G5 and G6 will be (B + BC) and (C + AB) respectively. Now, gate G7 is a 3-input AND Gate, therefore output (Y) of G7 will be equal to (A+AB). (B+BC). (C+AB)

现在，门G4是2输入或门，其输入之一为A，另一个为门G1的输出，因此门G4的输出为(A + AB)。 同样，门G5和G6的输出分别为(B + BC)和(C + AB)。 现在，门G7是3输入与门，因此G7的输出(Y)等于(A + AB)。 (B + BC)。 (C + AB)

Since, we have Y = (A+AB). (B+BC). (C+AB), now we have to minimize it.

因为，我们有Y =(A + AB)。 (B + BC)。 (C + AB) ，现在我们必须将其最小化。

    Therefore, (A+AB). (B+BC). (C+AB)
= A (1 + B). B (1 +C). (C+AB)
= A. B. (C+AB)		[Since, 1+B =1 and 1+C =1]
= AB (1 + C)
= AB

Therefore, Y=AB is the minimal expression. This can be implemented using a 2-input AND Gate having inputs A and B as:

因此， Y = AB是最小表达式 。 这可以使用具有输入A和B的2输入与门实现：

翻译自: https://www.includehelp.com/basics/realization-of-boolean-expressions-using-basic-logic-gates.aspx

java 逻辑表达式 布尔