离散点自动生成等高线

有限状态机 (Finite state machine)

A finite state machine (FSM) is similar to a finite state automation (FSA) except that the finite state machine "prints" an output using an output alphabet distinct from the input alphabet. The final definition is as follow:

有限状态机(FSM)与有限状态自动化(FSA)相似，区别在于有限状态机使用与输入字母不同的输出字母“打印”输出。 最终定义如下：

A finite state machine (also called complete sequential machine ) M( A, S, Z, S0, f, g) consists of six points.

有限状态机(也称为完全顺序机) M(A，S，Z，S0，f，g)由六个点组成。

1. A finite set A of input alphabet.

   输入字母的有限集A。

2. A finite set S of internal state.

   内部状态的有限集S。

3. A finite set z of output symbol.

   输出符号的有限集z 。

4. An initial state S0 in S.

   在S上的初始状态S0，

5. A next-state function f from S X A into S.

   从SXA到S的下一状态函数f 。

6. An output function g from S X A into Z.

   从SXA到Z的输出函数g 。

有限状态机的组成 (Components of finite state machine)

Input type

输入类型

The input type is divided into a square and each square contains a single symbol from the input alphabet X. The end squares of the tape contain end markers at the left end and $ at the right end. The absence of end markers in the input tape indicates that there is an infinite length of the tape. The left to right sequence of symbol between the end markers is the input string to be processed.

输入类型分为一个正方形，每个正方形包含来自输​​入字母X的单个符号。 磁带的方格在左端包含结束标记，在右端包含$ 。 输入磁带中没有结束标记，表明磁带长度无限。 结束标记之间从左到右的符号序列是要处理的输入字符串。

Reading head

阅读头

The head examines only one square at a time and can move on square either to the left or to the right. For further analysis are restrict the movement of R head only to the right side.

头部一次只检查一个正方形，并且可以在正方形上向左或向右移动。 为了进一步分析，仅将R头的移动限制在右侧。

Finite control

有限控制

The input to the finite control will be usually symboled under the R-head say a or the present state of the machine say q to give the following output:

有限控制的输入通常用R头表示a或机器的当前状态表示q来表示以下输出：

1. A motion of R head along the tape to the next square.

   R头沿磁带移动到下一个正方形。

2. The next state of the finite state machine given by & (q, a).

   ＆(q，a)给出的有限状态机的下一个状态。

Transition system

过渡系统

The finite labeled graph in which a state is represented by the vertex or node and the directed edges indicates the transition of a state and the edges are labeled with input/output is known as transition graph or a transition system.

其中状态由顶点或节点表示且有向边表示状态的转换且边缘以输入/输出标记的有限标记图称为转换图或转换系统。

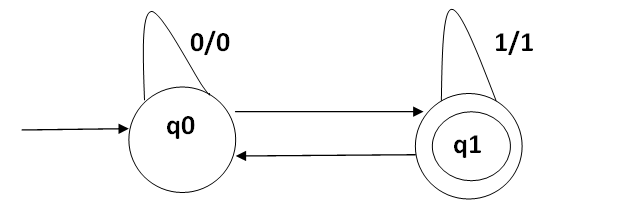
In the normal transition diagram, the initial state is represented by a circle with an arrow pointing towards it, the final state by two concentric circles and the other states are represented by just a circle.

在正常过渡图中，初始状态由带有箭头的圆形表示，最终状态由两个同心圆表示，其他状态仅由一个圆表示。

有限自动机的类型 (Types of finite Automata)

There are two types of finite automata:

有限自动机有两种类型：

1) Deterministic finite automata

1)确定性有限自动机

Some moves of the machine can be uniquely determined by the input symbol and present state. The DFA can be defined with 5 tuples (Q, X, &, q0, F). When,

机器的某些动作可以由输入符号和当前状态唯一地确定。 可以使用5个元组(Q，X，＆，q0，F)定义DFA。 什么时候，

• Q - is a finite non-empty set of states.

  Q-是有限的非空状态集。

• X - is a finite non-empty set of input called input alphabet.

  X-是一个有限的非空输入集，称为输入字母。

• & - is a function which maps Q x X into q and is usually called direct transition function. This is the function which describes the change of states driving the transition. This mapping is usually represented by a transition table or a transition diagram.

  ＆ -是将Q x X映射到q的函数，通常称为直接转移函数。 这是描述驱动过渡的状态变化的功能。 此映射通常由过渡表或过渡图表示。

• Qo E Q - is the initial state and,

  Qo EQ-是初始状态，

• F C Q - is the set of final states. It is assumed here that there may be more than one final state.

  FCQ-是最终状态集。 在此假设最终状态可能不止一个。

2) Non- deterministic finite Automata

2)非确定性有限自动机

Some moves of the machine can not uniquely determine by the input symbol and present state. The NDFA can be defined with 5 tuples. (Q, X, f, q0, F). Where,

机器的某些动作无法通过输入符号和当前状态唯一地确定。 NDFA可以定义为5个元组。 (Q，X，f，q0，F)。 哪里，

• Q - is a finite non-empty set of states.

  Q-是有限的非空状态集。

• X - is a finite non-empty set of inputs.

  X-是一组有限的非空输入。

• & - is the transition function mapping from Q x X into 2Q which is the power set of Q, the set of all subset of Q.

  ＆ -是从Q中的过渡函数映射X X成2Q是幂集Q，集合Q的所有子集中的。

• q0 E Q - is the initial state.

  q0 EQ-是初始状态。

• F C Q - is the set of final states.

  FCQ-是最终状态集。

The difference between the deterministic and non- deterministic automata is only in &. For deterministic automation, the outcome is a state i.e. an element of Q for non- deterministic automation the outcome is a subset of Q.

确定性自动机与非确定性自动机之间的区别仅在于＆ 。 对于确定性自动化，结果是状态，即Q的元素；对于非确定性自动化，结果是Q的子集。

翻译自: https://www.includehelp.com/basics/finite-automata.aspx

离散点自动生成等高线