排序，也称为排序算法，可以说是我们学习算法的过程中遇到的第一个门槛，也是实际应用中使用得较为频繁的算法，我将自己对所学的排序算法进行一个归纳总结与分享，如有错误，欢迎指正！

排序算法学习分享（一）选择排序

排序算法学习分享（二）交换排序---冒泡排序与快速排序

排序算法学习分享（三）插入排序

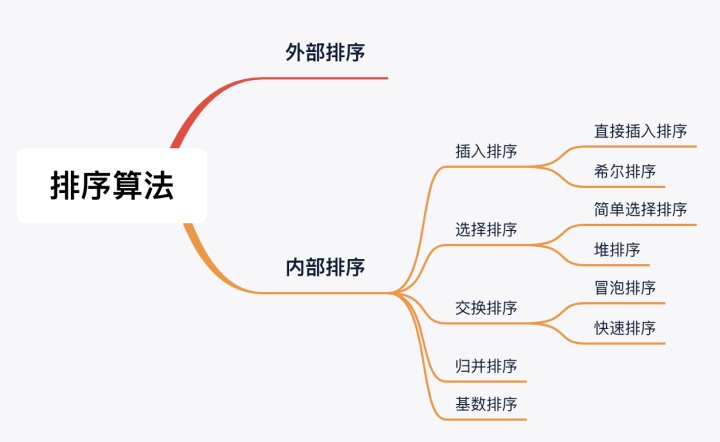
（一）排序的分类

排序算法主要分为内部排序与外部排序，当数据量大时，数据无法全部加载到内存中，因此需要接抓外部存储（文件、磁盘等）进行排序。而内部排序则是指将要处理的所有数据加载到内部存储器中，并在内存中就完成排序。

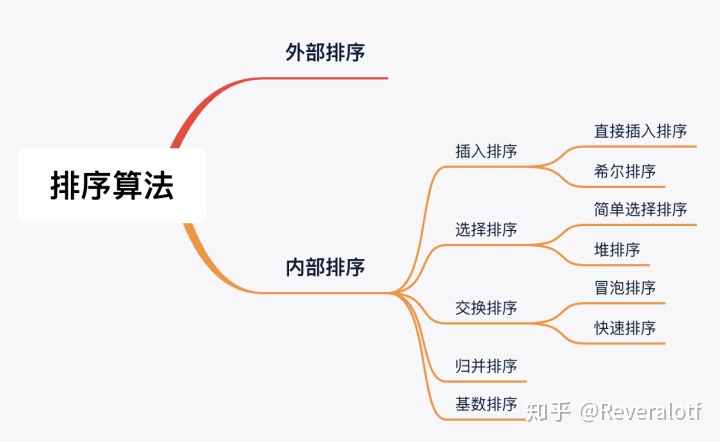
本文针对的为内部排序。

（二）内部排序

4 希尔排序

前文我介绍了插入排序，但是插入排序会出现一个问题。如果我们拿到的是一个较小的数进行插入排序，那么元素后移的次数会明显增加，那么就会严重影响整个排序的效率。

接下来介绍的希尔排序就是经典的对插入排序的一种优化。

希尔排序，也称递减增量排序，是插入排序的一种更高效的改进版本。我们都知道，插入排序对已经有序的或者是有序程度高的序列排序是非常快的，但一般情况下，由于插入排序每插入一个元素都只能一个一个元素地进行移动，因此它的效率是十分低下的。

显然要优化插入排序的移动是很困难的，而希尔排序取巧地不去优化它的移动，希尔排序的思想我用一句话去概括：尽可能的在数组进行下一轮的排序时，提高数组的有序程度。

先记住一点：在序列的排序中，元素越少，需要交换的次数越少，排序越快。

那么怎么去提高一个数组的有序程度呢？用一个很有趣的东西——增量。

这类似于分治思想，但它又不是。希尔排序利用增量这一个东西去将序列分割成若干个子序列，再将每个子序列分别排好。 那么究竟什么是增量？又要怎么利用增量？

增量就是一个等差数列的差值，比如1,3,5,7,9。它们的增量是2。一开始尽可能使用一个大的增量，使得每个子序列中的元素少，比如第一轮就尽量使得一个子序列的元素只有两个。

增量越大，那么分的组就会越多，每个组中的元素数目就会小。每一轮都比上一轮的增量按照一定的规律递减，那么分的组就会比上一轮的分的组少，而每个组中的元素就要比上一轮的元素要多，当增量一直减到1的时候，我们就会发现只有一个组了，而这个组中的元素就是整个序列的所有元素，这就是递减增量。

利用增量这样子分割序列是为了什么呢？是为了使下一轮的有序程度变高。为什么我说希尔排序是一种取巧呢？就是因为它耍赖皮，有序程度低的时候，增量就大，分组就多，组内元素就少，排序就快。当这一轮排序完成的时候，全体序列的有序程度一定是要比上一轮的有序程度要高的（有一些特殊情况，严谨地应该说是不低于）。

增量每一次发生递减，那么序列的有序程度就提高了那么一点，当增量递减到1的时候，序列的有序程度就已经很高的，这时再进行一轮插入排序，就很快了。

这么将还是有些抽象，我们举一个实例，上一些图来说明。

这是一个原始数组，可以看到它的有序程度并不高。

我们对它进行第一次增量分组，使得每组中的元素尽可能少。最少的话是一个元素一个组，但是如果组中只有一个元素，那么组内的排序根本没有意义，因此第一次的这个尽可能少，就是两两一组。此时的增量为4。

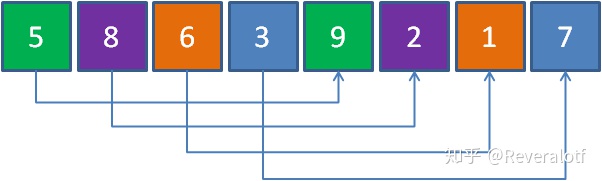
我们对每个子数组内进行排序。由于每个子数组内的元素很少，因此排序很快，排序完如下：

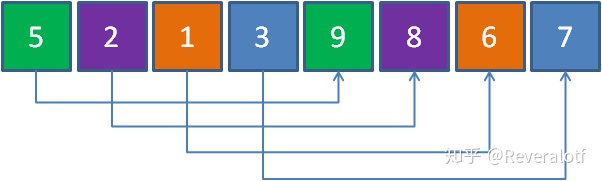
我们已经可以看到只是经过简单的几个交换后数组的有序程度就已经显著提升了，那么接下来就是进入到下一轮。

递减增量，直接使增量减半(希尔增量)，新的增量为4 / 2 = 2，将2作为新的增量重新进行分组，分组如下。

我们对每个分组内进行排序，因为经过了上一轮的排序，可以看到每个组内的有序程度比上一轮如果也按照这个增量分组的有序程度要高。

这就达到了希尔排序的目的，就是每一轮都要比上一轮的有序程度要高，这很像我们做产品时候的不断迭代。

排序好后如下：

这一轮结束后增量再递减就变成1了，最后再进行一轮插入排序即可，此时需要移动的数仅仅就是5和3，8和9。有序程度比原数组高到不知道哪里去了。再来一轮插入排序就完成啦！

其实递减增量的规则有很多种，不止折半这一种，有时候根据需求改变递减增量的方式会取得更优的性能。

下面尝试用代码实现希尔排序:

希尔排序使用的增量是折半的方式递减的，这种方式的增量叫做希尔增量。希尔排序利用增量分组粗调一般情况下是减少了插入排序的工作量，使得插入排序的时间复杂度低于O(n²)。

但是，在一种极端的情况下，希尔排序所做的粗略调整不但没有减少插入排序的工作量，反而增大的插入排序的工作量。

举一个例子：

我们利用希尔增量来分组，当增量为4时，分组为：（2，7），（1，6），（5，9），（3，8）。我们可以看到它在组内是有序的，再折半减少增量为2，分组为（2，5，7，9），（1，3，6，8），还是有序的，经过两轮增量排序，它的有序程度并没有提高，比起直接插入排序反而还增加分组排序的这一个步骤，增加了工作量。

会出现这种情况的原因在于希尔增量，希尔增量之间是等比的，这代表着等比之间是可以出现一定的盲区的，就像上面这个例子，就完美地处在了希尔增量之间的盲区。

那么才能使得增量之间没有盲区呢？最好的方式就是使得每一轮彼此的增量“互质”。而增量的方式很多，最为典型的就是Hibbard增量和Sedgewick增量。因为本文讲的是希尔排序，就不继续往下介绍了。

希尔排序是一个不稳定的排序算法，是因为在分组的过程中，两个元素的交换的跨度有时候是会很大的。比如m > i = j > k，而原数组是( i ，j ，k ，m )，那么第一轮希尔排序后，i 就到 j 后面了。

希尔排序的介绍就到这里啦！希尔排序的中心思想就是: 尽可能的在数组进行下一轮的排序前，提高数组的有序程度。即每一轮都比上一轮时候的有序程度要高。