点击上方蓝色字体,关注AI小白入门哟

作者 | 文杰
编辑 | yuquanle
本文介绍线性回归模型,从梯度下降和最小二乘的角度来求解线性回归问题,以概率的方式解释了线性回归为什么采用平方损失,然后介绍了线性回归中常用的两种范数来解决过拟合和矩阵不可逆的情况,分别对应岭回归和Lasso回归,最后考虑到线性回归的局限性,介绍了一种局部加权线性回归,增加其非线性表示能力
线性回归
A、线性回归
假设有数据有:
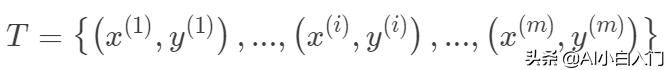
其中
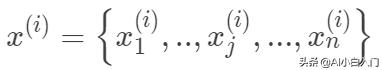
,
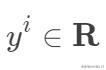
。其中m为训练集样本数,n为样本维度,y是样本的真实值。线性回归采用一个高维的线性函数来尽可能的拟合所有的数据点,最简单的想法就是最小化函数值与真实值误差的平方(概率解释-高斯分布加最大似然估计)。即有如下目标函数:
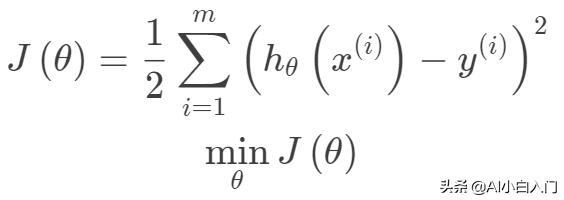
其中线性函数如下:
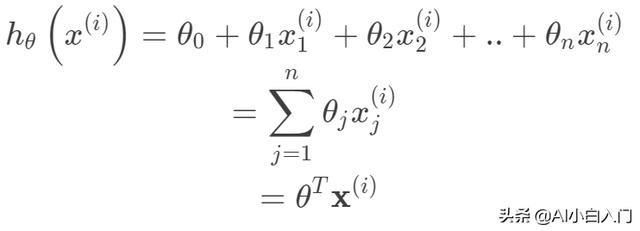
构建好线性回归模型的目标函数之后,接下来就是求解目标函数的最优解,即一个优化问题。常用的梯度优化方法都可以拿来用,这里以梯度下降法来求解目标函数。
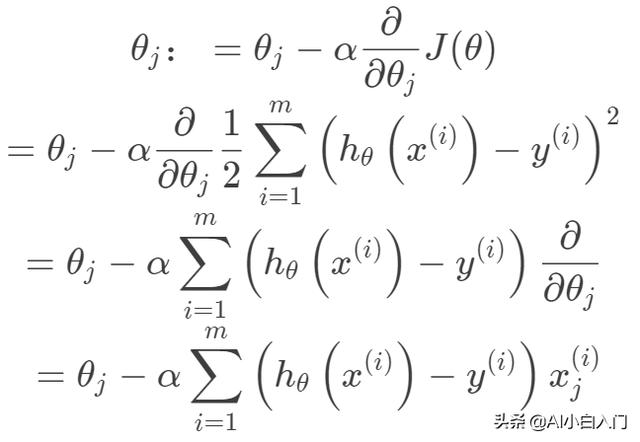
另外,线性回归也可以从最小二乘法的角度来看,下面先将样本表示向量化,
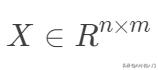
,
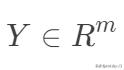
,构成如下数据矩阵。
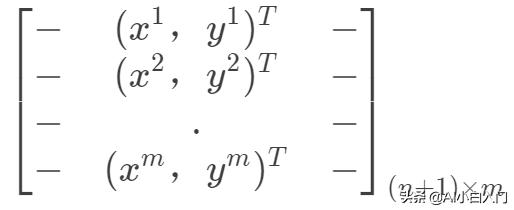
那么目标函数向量化形式如下:
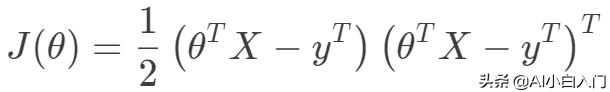
可以看出目标函数是一个凸二次规划问题,其最优解在导数为0处取到。
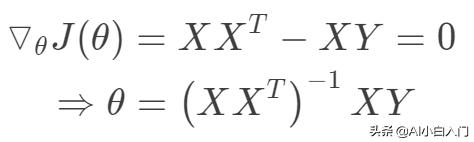
值得注意的上式中存在计算矩阵的逆,一般来讲当样本数大于数据维度时,矩阵可逆,可以采用最小二乘法求得目标函数的闭式解。当数据维度大于样本数时,矩阵线性相关,不可逆。此时最小化目标函数解不唯一,且非常多,出于这样一种情况,我们可以考虑奥卡姆剃刀准则来简化模型复杂度,使其不必要的特征对应的w为0。所以引入正则项使得模型中w非0个数最少。当然,岭回归,lasso回归的最根本的目的不是解决不可逆问题,而是防止过拟合。
B、概率解释
损失函数与最小二乘法采用最小化平方和的概率解释。假设模型预测值与真实值的误差为
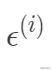
,那么预测值
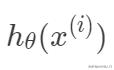
与真实值
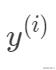
之间有如下关系:
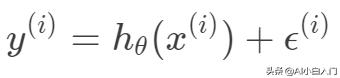
根据中心极限定理,当一个事件与很多独立随机变量有关,该事件服从正态分布 。一般来说,连续值我们都倾向于假设服从正态分布。假设每个样本的误差
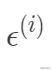
独立同分布均值为0,方差为σ的高斯分布
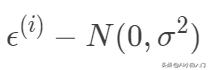
,所以有:
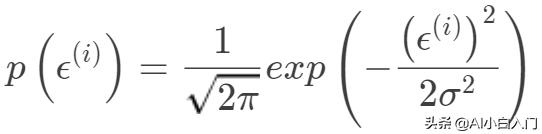
即表示
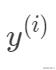
满足以均值为
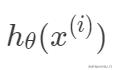
,方差为
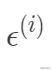
的高斯分布。
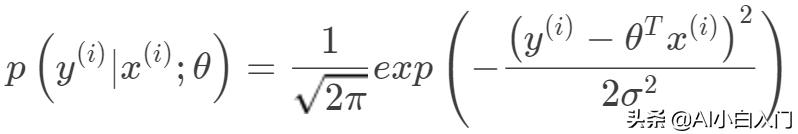
由最大似然估计有:
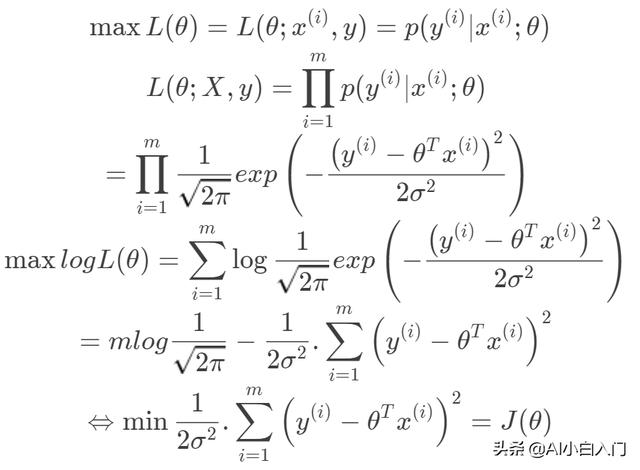
岭回归和Lasso回归
岭回归的目标函数在一般的线性回归的基础上加入了正则项,在保证最佳拟合误差的同时,使得参数尽可能的“简单”,使得模型的泛化能力强(即不过分相信从训练数据中学到的知识)。正则项一般采用一,二范数,使得模型更具有泛化性,同时可以解决线性回归中不可逆情况。
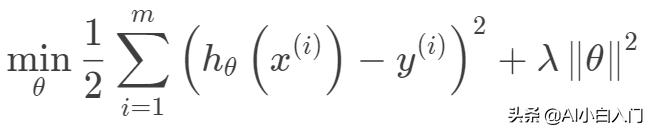
其迭代优化函数如下:
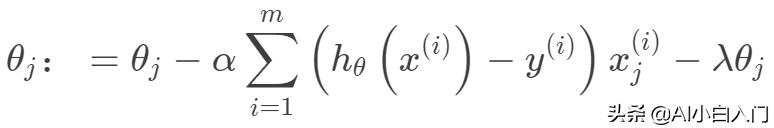
另外从最小二乘的角度来看,通过引入二范正则项,使其主对角线元素来强制矩阵可逆。
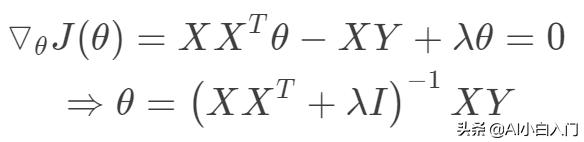
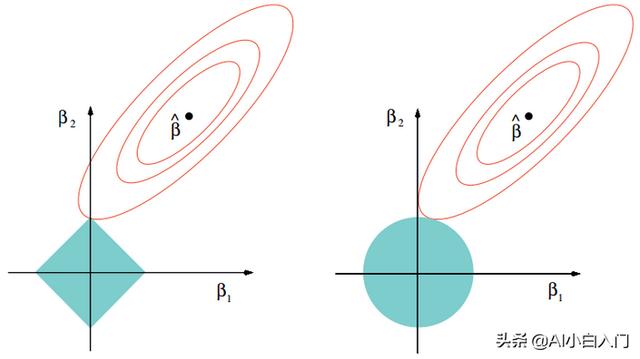
Lasso回归采用一范数来约束,使参数非零个数最少。而Lasso和岭回归的区别很好理解,在优化过程中,最优解为函数等值线与约束空间的交集,正则项可以看作是约束空间。可以看出二范的约束空间是一个球形,而一范的约束空间是一个方形,这也就是二范会得到很多参数接近0的值,而一范则尽可能非零参数最少。
值得注意的是线性模型的表示能力有限,但是并不一定表示线性模型只能处理线性分布的数据。这里有两种常用的线性模型非线性化。对于上面的线性函数的构造,我们可以看出模型在以
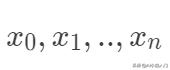
的坐标上是线性的,但是并不表示线性的模型就一定只能用于线性分布问题上。假如我们只有一个特征
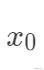
,而实际上回归值是
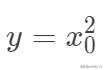
等,我们同样可以采用线性模型,因为我们完全可以把输入空间映射到高维空间
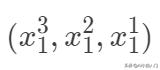
,其实这也是核方法以及PCA空间变换的一种思想,凡是对输入空间进行线性,非线性的变换,都是把输入空间映射到特征空间的思想,所以只需要把非线性问题转化为线性问题即可。另外一种是局部线性思想,即对每一个样本构建一个加权的线性模型。
局部加权线性回归
考虑到线性回归的表示能力有限,可能出现欠拟合现象。局部加权线性回归为每一个待预测的点构建一个加权的线性模型。其加权的方式是根据预测点与数据集中点的距离来为数据集中的点赋权重,当某点距离预测点较远时,其权重较小,反之较大。由于这种权重的机制引入使得局部加权线性回归产生了一种局部分段拟合的效果。由于该方法对于每一个预测点构建一个加权线性模型,都要重新计算与数据集中所有点的距离来确定权重值,进而确定针对该预测点的线性模型,计算成本高,同时为了实现无参估计来计算权重,需要存储整个数据集。
局部加权线性回归,在线性回归基础上引入权重,其目标函数(下面的目标函数是针对一个预测样本的)如下:
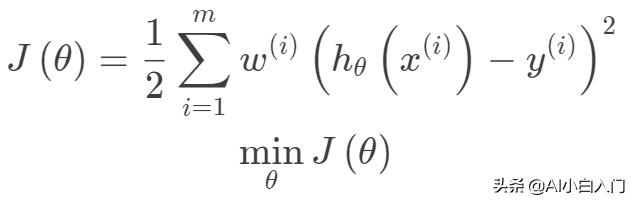
一般选择下面的权重函数,权重函数选择并非因为其类似于高斯函数,而是根据数据分布的特性,但权重函数的选取并不一定依赖于数据特性。
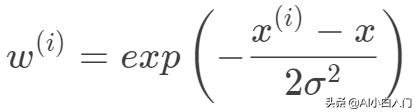
其中是待预测的一个数据点。
对于上面的目标函数,我们的目标同样是求解使得损失函数最小化,同样局部加权线性回归可以采用梯度的方法,也可以从最小二乘法的角度给出闭式解。
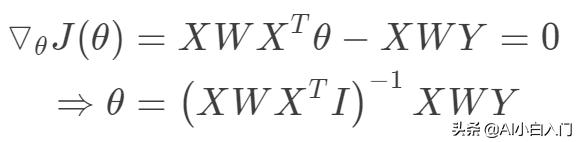
其中
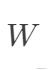
是对角矩阵,
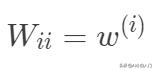
。
线性回归核心思想最小化平方误差,可以从最小化损失函数和最小二乘角度来看,优化过程可以采用梯度方法和闭式解。在闭式解问题中需要注意矩阵可逆问题。考虑到过拟合和欠拟合问题,有岭回归和lasso回归来防止过拟合,局部加权线性回归通过加权实现非线性表示。
代码实战
A、线性回归
/**线性回归函数的实现,考虑一般的线性回归,最小平方和作为损失函数,则目标函数是一个无约束的凸二次规划问题,由凸二次规划问题的极小值在导数为0处取到,且极小值为全局最小值,且有闭式解。根据数学表达式实现矩阵之间的运算求得参数w。**/int regression(Matrix x,Matrix y){ Matrix xT=x.transposeMatrix(); Matrix xTx=xTx.multsMatrix(xT,x); Matrix xTx_1=xTx.niMatrix(); Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT); Matrix ws; ws=ws.multsMatrix(xTx_1xT,y); cout<B、岭回归和Lasso回归
/**下面的岭回归函数只是在一般的线性回归函数的基础上在对角线上引入了岭的概念,不仅有解决矩阵不可逆的线性,同样也有正则项的目的,采用常用的二范数就得到了直接引入lam的形式。**/int ridgeRegres(Matrix x,Matrix y,double lam){ Matrix xT=x.transposeMatrix(); Matrix xTx=xTx.multsMatrix(xT,x); Matrix denom(xTx.row,xTx.col,lam,"diag"); xTx=xTx.addMatrix(xTx,denom); Matrix xTx_1=xTx.niMatrix(); Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT); Matrix ws=ws.multsMatrix(xTx_1xT,y); cout<C、局部加权线性回归
/**局部加权线性回归是在线性回归的基础上对每一个测试样本(训练的时候就是每一个训练样本)在其已有的样本进行一个加权拟合,权重的确定可以通过一个核来计算,常用的有高斯核(离测试样本越近,权重越大,反之越小),这样对每一个测试样本就得到了不一样的权重向量,所以最后得出的拟合曲线不再是线性的了,这样就增加的模型的复杂度来更好的拟合非线性数据。**///需要注意的是局部加权线性回归是对每一个样本进行权重计算,所以对于每一个样本都有一个权重w,所以下面的函数只是局部线性回归的一个主要辅助函数Matrix locWeightLineReg(Matrix test,Matrix x,Matrix y,const double &k){ Matrix w(x.row,x.row,0,"T"); double temp=0; int i,j; /** 根据测试样本点与整个样本的距离已经选择的核确定局部加权矩阵,采用对角线上为局部加权值 **/ for(i=0;i详细代码: https://github.com/myazi/myLearn/blob/master/LineReg.cpp
The End







)








)


