堆其实就是一种特殊的队列——优先队列。
普通的队列游戏规则很简单:就是先进先出;但这种优先队列搞特殊,不是按照进队列的时间顺序,而是按照每个元素的优先级来比拼,优先级高的在堆顶。
这也很容易理解吧,比如各种软件都有会员制度,某软件用了会员就能加速下载的,不同等级的会员速度还不一样,那就是优先级不同呀。
还有其实每个人回复微信消息也是默默的把消息放进堆里排个序:先回男朋友女朋友的,然后再回其他人的。
这里要区别于操作系统里的那个“堆”,这两个虽然都叫堆,但是没有半毛钱关系,都是借用了 Heap 这个英文单词而已。
我们再来回顾一下「堆」在整个 Java 集合框架中的位置:
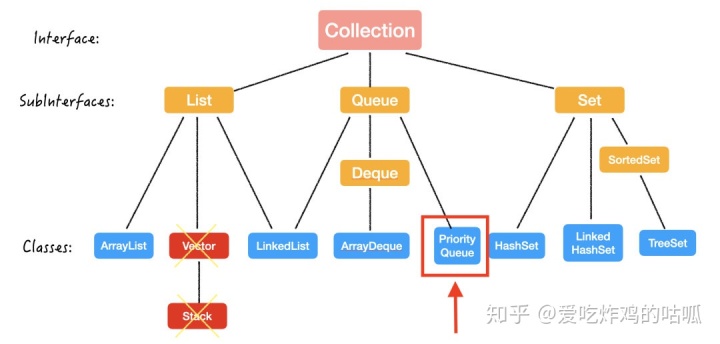
也就是说,
- PriorityQueue 是一个类 (class);
- PriorityQueue 继承自 Queue 这个接口 (Interface);
那 heap 在哪呢?
heap 其实是一个抽象的数据结构,或者说是逻辑上的数据结构,并不是一个物理上真实存在的数据结构。
heap 其实有很多种实现方式,比如 binomial heap, Fibonacci heap 等等。但是面试最常考的,也是最经典的,就是 binary heap 二叉堆,也就是用一棵完全二叉树来实现的。
那完全二叉树是怎么实现的?
其实是用数组来实现的!所以 binary heap/PriorityQueue 实际上是用数组来实现的。
这个数组的排列方式有点特别,因为它总会维护你定义的(或者默认的)优先级最高的元素在数组的首位,所以不是随便一个数组都叫「堆」,实际上,它在你心里,应该是一棵「完全二叉树」。
这棵完全二叉树,只存在你心里和各大书本上;实际在在内存里,哪有什么树?就是数组罢了。
那为什么完全二叉树可以用数组来实现?是不是所有的树都能用数组来实现?
这个就涉及完全二叉树的性质了,我们下一篇会细讲,简单来说,因为完全二叉树的定义要求了它在层序遍历的时候没有气泡,也就是连续存储的,所以可以用数组来存放;第二个问题当然是否。堆的特点
- 堆是一棵完全二叉树;
- 堆序性 (heap order): 任意节点都优于它的所有孩子。
a. 如果是任意节点都大于它的所有孩子,这样的堆叫大顶堆,Max Heap;
b. 如果是任意节点都小于它的所有孩子,这样的堆叫小顶堆,Min Heap;
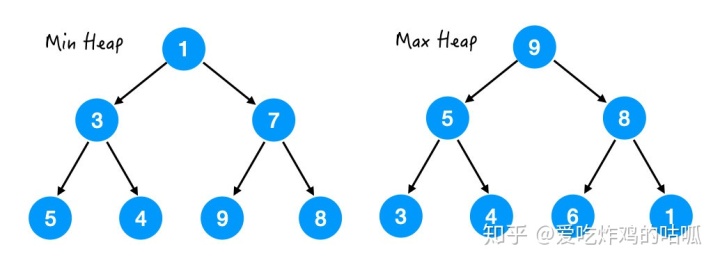
左图是小顶堆,可以看出对于每个节点来说,都是小于它的所有孩子的,注意是所有孩子,包括孙子,曾孙...
- 既然堆是用数组来实现的,那么我们可以找到每个节点和它的父母/孩子之间的关系,从而可以直接访问到它们。
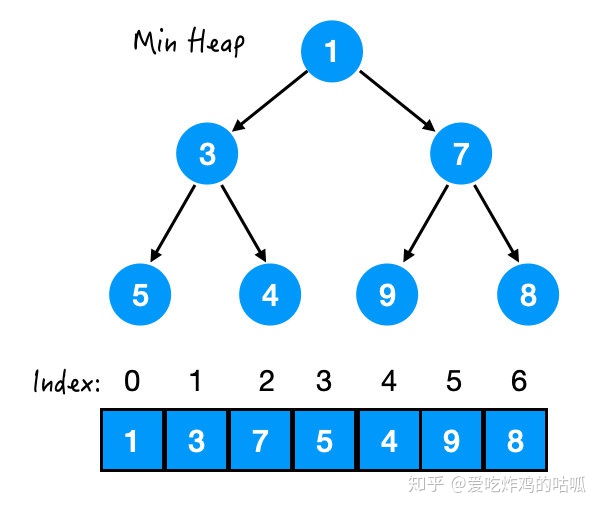
比如对于节点 3 来说,
- 它的 Index = 1,
- 它的 parent index = 0,
- 左孩子 left child index = 3,
- 右孩子 right child index = 4.
可以归纳出如下规律:
- 设当前节点的 index = x,
- 那么 parent index = (x-1)/2,
- 左孩子 left child index = 2*x + 1,
- 右孩子 right child index = 2*x + 2.
有些书上可能写法稍有不同,是因为它们的数组是从 1 开始的,而我这里数组的下标是从 0 开始的,都是可以的。
这样就可以从任意一个点,一步找到它的孙子、曾孙子,真的太方便了,在之后讲具体操作时大家可以更深刻的体会到。
那有关堆的基本操作,以及为什么 heapify() 是 O(n) 的,我们之后再聊。
作者:是小齐呀
链接:https://juejin.im/post/6880291677651599367




)








)





