【算法精讲】分享一道很不错的算法题

戳蓝字“CSDN云计算”关注我们哦！

640?wx_fmt=jpeg

技术头条：干货、简洁、多维全面。更多云计算精华知识尽在眼前，get要点、solve难题，统统不在话下！

作者：帅地

转自：苦逼的码农

分享一道leetcode上的题，当然，居然不是放在刷题贴里来讲，意味着分享的这道题不仅仅是教你怎么来解决，更重要的是这道题引发出来的一些解题技巧或许可以用在其他地方，下面我们来看看这道题的描述。

问题描述

给定一个未排序的整数数组，找出其中没有出现的最小的正整数。

示例 1:

输入: [1,2,0]
输出: 3
示例 2:

输入: [3,4,-1,1]
输出: 2
示例 3:

输入: [7,8,9,11,12]
输出: 1

说明: 你的算法的时间复杂度应为O(n)，并且只能使用常数级别的空间。

解答

这道题在 leetcode 的定位是困难级别，或许你可以尝试自己做一下，然后再来看我的解答，下面面我一步步来分析，秒杀的大佬请忽略…..

对于一道题，如果不能第一时间想到最优方案时，我觉得可以先不用那么严格，可以先采用暴力的方法求解出来，然后再来一步步优化。像这道题，我想，如果可以你要先用快速排序先把他们排序，然后在再来求解的话，那是相当容易的，不过 O(nlogn) 的时间复杂度太高，其实我们可以先牺牲下我们的空间复杂度，让保证我们的时间复杂度为 O(n)，之后再来慢慢优化我们的空间复杂度。

方法一：采用集合

我们知道，如果数组的长度为 n，那么我们要找的目标数一定是出于 1~n+1 之间的，我们可以先把我们数组里的所有数映射到集合里，然后我们从 1~n 开始遍历判断，看看哪个数是没有在集合的，如果不存在的话，那么这个数便是我们要找的数了。如果 1~n 都存在，那我们要找的数就是 n+1 了。

不过这里需要注意的是，在把数组里面的数存进集合的时候，对于小于 1 或者大于 n 的数，我们是不需要存进集合里的，因为他们不会对结果造成影响，这也算是一种优化吧。光说还不行，还得会写代码，代码如下：

    public int firstMissingPositive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] >= 1 && nums[i] <= n) {
                set.add(nums[i]);
            }
        }
        for (int i = 1; i <= n; i++) {
            if (!set.contains(i)) {
                return  i;
            }
        }
        return n + 1;
    }

采用 bitmap

方法一的空间复杂度在最块的情况下是 O(n)，不知道大家还记不记得位算法，其实我们是可以利用位算法来继续优化我们的空间的，如果不知道位算法的可以看我直接写的一篇文章：

1、[什么是bitmap算法]()。

2、[自己用代码实现bitmap算法]();

通过采用位算法，我们我们把空间复杂度减少32倍，即从 O(n) -> O(n/32)，但其实 O(n/32) 任然还算 O(n)，不过，在实际运行的时候，它是确实能够让我们运行的更快的，在 Java 中，已经有自带的支持位算法的类了，即 bitSet，如果你没学过这个类，我相信你也是能一眼看懂的，代码如下：

    public int firstMissingPositive2(int[] nums) {
        BitSet bitSet = new BitSet();
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] >= 1 && nums[i] <= n) {
                bitSet.set(nums[i]);
            }
        }
        for (int i = 1; i <= n; i++) {
            if (!bitSet.get(i)) {
                return  i;
            }
        }
        return n + 1;
    }

方法3：最终版本

如果这个数组是有序的，那就好办了，但是如果我们要把它进行排序的话，又得需要 O(nlogn) 的时间复杂度，那我们有没有啥办法把它进行排序，然后时间复杂度又不需要那么高呢？

答是可以，刚才我们说过，对于那些小于 1 或者大于 n 的数，我们是其实是可以不理的，居然我们，我们需要处理的这些数，他们都是处于 1~n 之间的，那要你给这些处于 1~n 之间的数排序，并且重复的元素我们也是可以忽略掉的，记录一个就可以了，那么你能不能在 O(n) 时间复杂度排序好呢？

不知道大家是否还记得我之间写过的下标法？

[一些常用的算法技巧总结]()。

或者是否还记得计数排序？（计数排序其实就是下标法的一个应用了）

不过学过计数排序的朋友可能都知道，计数排序是需要我们开一个新的数组的，不过我们这里不需要，这道题我们可以这样做：例如对于 nums[i]，我们可以把它放到数组下标位 nums[i] - 1 的位置上，这样子一处理的话，所有 1<=nums[i]<=n 的数，就都是是处于相对有序的位置了。注意，我指的是相对，也就是说对于 1-n 这些数而言，其他小于 1 或者大于 n 的我们不理的。例如对于这个数组 nums[] = {4, 1, -1, 3, 7}。

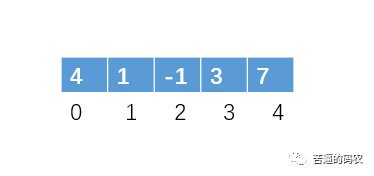
让 nums[i] 放到数组下标为 nums[i-1]的位置，并且对于那些 nums[i]<=0 或 nums > n的数，我们是可以不用理的，所以过程如下：从下标为 0 开始向右遍历

1、把 4 放在下标为 3 的位置，为了不让下标为 3 的数丢失，把下标为 3 的数与 4进行交换。

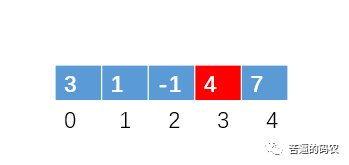
2、此时我们还不能向右移动来处下标为1的数，因为我们当前位置的3还不是处于有序的位置，还得继续处理，所以把 3 与下标为 2 的数交换

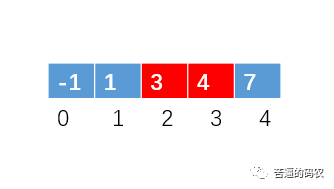
3、当前位置额数为 -1，不理它，前进到下标为 1 的位置，把 1 与下标为 0的数交换

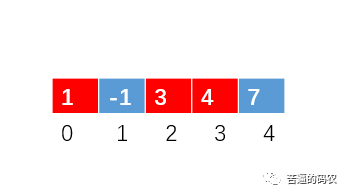
4、当前位置额数为 -1，不理它，前进到下标为 2 的位置，此时的 3 处于有序的位置，不理它继续前进，4也是处于有序的位置，继续前进。

5、此时的 7 > n，不理它，继续前进。

遍历完成，此时，那些处于 1~n的数都是处于有序的位置了，对于那些小于1或者大于n的，我们忽略它假装没看到就是了。

这里还有个要注意的地方，就是 nums[i] 与下标为 nums[i]-1的数如果相等的话也是不需要交换的。

接下来，我们再次从下标 0 到下标 n-1 遍历这个数组，如果遇到 nums[i] != i + 1 的数，，那么这个时候我们就找到目标数了，即 i + 1。

好吧，我觉得我讲的有点啰嗦了，还一步步话题展现过程给你们看，连我自己都感觉有点啰嗦了，大佬勿喷哈。最后代码如下：

    public int firstMissingPositive(int[] nums) {
        if(nums == null || nums.length < 1)
            return 1;
        int n = nums.length;
        for(int i = 0; i < n; i++){
            // 这里还有个要注意的地方，就是 nums[i] 与下标为 nums[i]-1的数如果相等的话
            // 也是不需要交换的。
            while(nums[i] >= 1 && nums[i] <= n && nums[i] != i + 1 && nums[i] != nums[nums[i]-1] ){
                // 和下标为 nums[i] - 1的数进行交换
                int tmp = nums[i];
                nums[i] = nums[tmp - 1];
                nums[tmp - 1] = tmp;
            }
        }
        for(int i = 0; i < n; i++){
            if(nums[i] != i + 1){
                return i + 1;
            }
        }
        return n + 1;
    }