摘要： 一项优化神经网络的技术，点进来了解一下？

认识上图这些人吗？这些人把自己叫做“The Myth Busters”，为什么？在他们的启发下，我们才会在Paperspace做类似的事情。我们要解决是Batch Normalization（BN）是否确实解决了Internal Covariate Shift的问题。虽然Batch Normalization已经存在了几年，并且已经成为深度神经网络的主要内容，但它仍然是深度学习中最容易被误解的概念之一。

Batch Normalization真的解决了Internal Covariate Shift问题了吗？它是用来做什么的？你所学的深度学习是真的吗？我们来看看吧！

在开始之前

我们曾经讨论过：

1、如何利用随机梯度下降来解决深度学习中局部极小值和鞍点的问题。

2、Momentum（动量）和Adam（自适应矩估计）等优化算法如何增强梯度下降以解决优化曲面中的曲率问题。

3、如何使用不同的激活函数来解决梯度消失问题。

为了有效地学习神经网络，神经网络的每一层分布都应该：均值为0、始终保持相同的分布；第二个条件意味着通过批梯度下降输入到网路层的数据分布不应该变化太多，并且随着训练的进行它应该保持不变，而不是每一层的分布都在发生变化。

Internal Covariate Shift

 Batch Normalization：通过减少Internal Covariate Shift来加快深度网络训练，其前提是解决一个称为Internal Covariate Shift的问题。

就像我们现在所称的那样，Internal Covariate Shift是指在训练过程中，隐层的输入分布老是变来变去，Internal指的是深层网络的隐层，是发生在网络内部的事情，Covariate指的是输入分布被变化的权重参数化，Shift指分布正在发生变化。

所以，让我们试着观察这件事情怎样发生的。再次，尽可能想象一下最简单的神经网络之一：线性堆叠的神经元，这样你也可以通过替换神经元网络层来扩展类比。

 

假设我们正在优化损失函数L,神经元d权重的更新规则是：

我们可以看到权重d的梯度取决于c的输出，对于神经网络中的任何层也是如此。神经元的权重梯度取决于它的输入或者下一层的输出。

然后梯度向着反方向更新权重，此过程一直重复，让我们回到d层，因为我们对d进行了梯度更新，我们期望omega_d可以有更小的损失，然而并非如此，让我们看一下原因。

我们从i开始进行初始迭代更新。假设输出c在迭代i为p_c^i ，d层更新不妨假设c的输入分布为p_c^i。在向下传递期间，c，omega_c的权重也会更新，这导致c的输出分布发生变化。在下一次迭代i+1中，假设z_c的分布已转变到p_c^{i+1}。由于d层的权重是根据p_c^i更新的，现在d层对应输入分布p_c^{i+1}，这种差异可能导致网络层产生根本不会减少损失的输出。

现在，我们可以提出两个问题：

输入分布的变化究竟如何使神经网络层更难学习？

这种分布的变化是否足够引起上述情况？

我们先回答第一个问题：

为什么Internal Covariate Shift造成上述情况？

神经网络的作用是生成映射f，将输入x映射到输出y。x的分布发生变化，为什么会使神经网络层更难学习？

下图为x标准分布图：

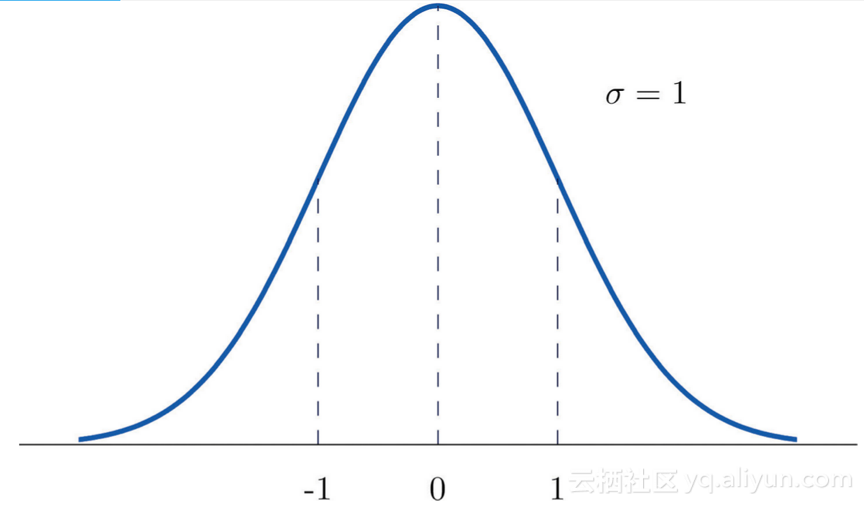
x的非标准分布如下图：

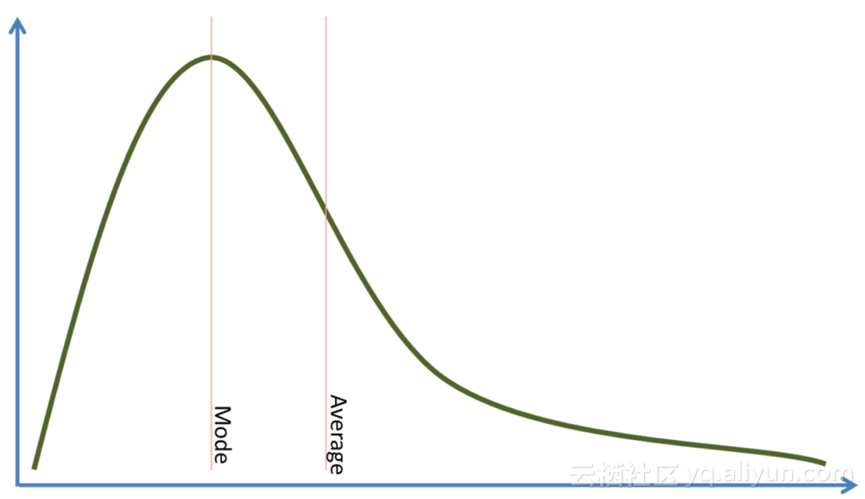
假设我们正在尝试的映射是f=2x，如果x的分布在一个地方压缩了很多密度，或者它是否均匀分布为什么那么重要？

事实证明，这很重要，现代精确的深层网络，是非常强大的曲线拟合器。假设我们有一个l层，对应输入为x，其分布如下。另外，我们假设，由层l学习的函数，由虚线表示：

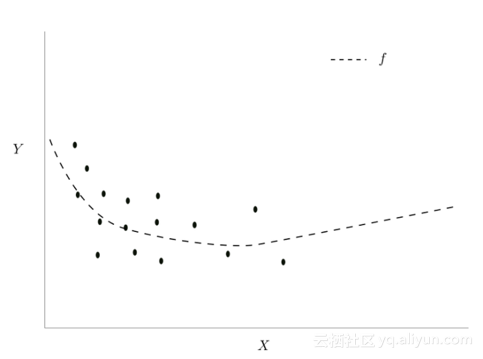
i的迭代

假设在梯度更新之后，当到下一层网络小批量梯度下降时，x的分布变为这样:

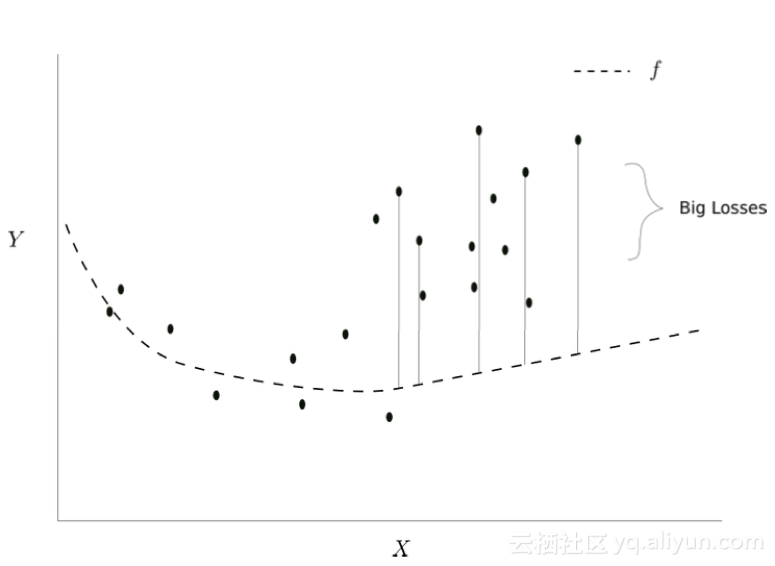
i+1迭代

注意这个小批量梯度下降的损失与之前的损失相比更多，为什么会这样？让我们回到我们之前的数据,我们最初学到的映射f可以很好地减少之前小批量梯度下降的损失。对于许多其他函数也是如此，在x不密集的区域中，这些函数差别很大。

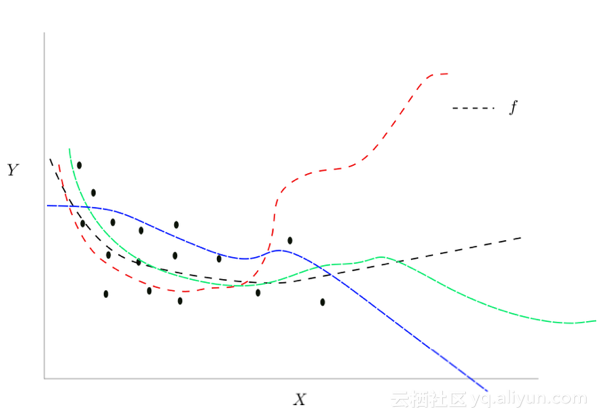
适应相同输入xi的不同函数

如果我们选择红色虚线给出的函数，下一个小批量梯度下降的损失也会很低。

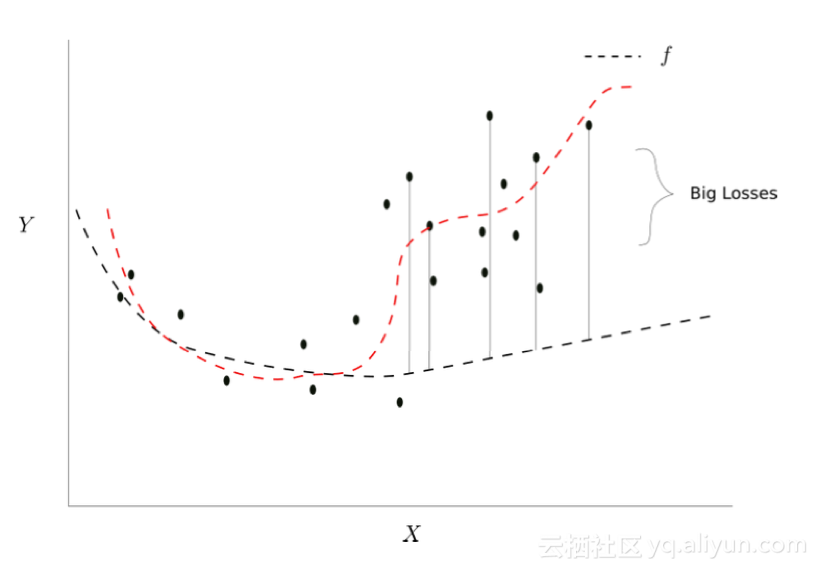
更合适的另一个函数

现在明显的问题是我们如何修改我们的算法，以便我们最终学习的映射对应红色虚线的映射？没有简单的答案，对于这种情况更好的办法是预防它们而不是等这种情况发生了再去解决它。

ICS最终搞砸我们学习的原因是我们的神经网络总是在输入分布的密集区域上表现更好。由于较密集区域中的数据点主导平均损失（我们试图最小化），因此密集区域中点的损失减少得更多。

但是，如果ICS最终在训练期间的后续批次中更改输入分布的密集区域，则网络在之前迭代期间学习的权重不再是最佳的。它可能需要非常仔细地调整超参数来获得合理的学习。这就解释了为什么ICS会出现这样的问题。

我们所说的是在小批量梯度下降中存在很大的方差。方差确保我们的映射不会在输入分布的一个区域中过度专门化，我们也希望均值在零附近。

规范化输入

解决此问题的一种方法是将输入归一化到神经网络，以使输入分布均值为0和方差为1。但是，这仅适用于网络不够深的情况。当网络变得更深，比如20层或更多层时，即使输入被归一化，超过20多个层的权重的微小波动也会导致输入到更深层的输入分布发生很大变化。

例如语言变化（不完全正确）：我们旅行距离发生变化，语言也会发生变化。 但是，较短距离内的语言有很多相似之处。比如西班牙语和葡萄牙语，它们都源于史前印欧语言。印度斯坦语也是如此，印度语是8000公里以外的地方。 但是，西班牙语和印度斯坦语之间的差异比西班牙语和葡萄牙语之间的差异要大得多。原因是小距离的微小变化已经放大了很多，深度网络也是如此。

输入批量归一化

我们现在介绍批量归一化的概念，它实际上规范了网络层的输出激活，然后做了更多的事情，下面是详细的描述：

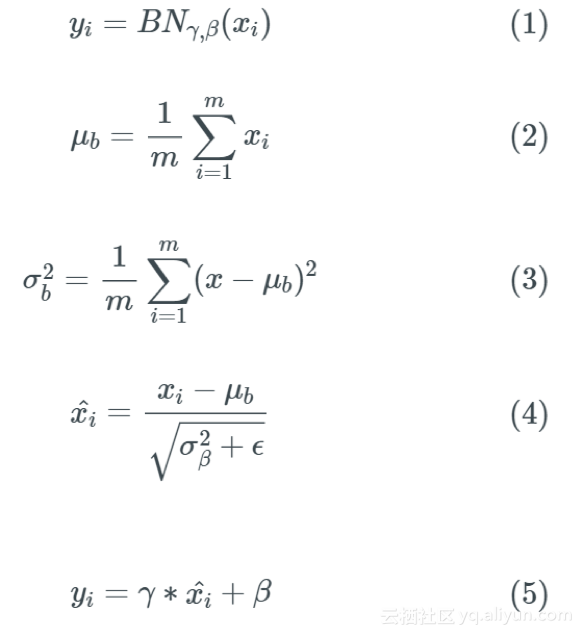
上述等式描述了BatchNorm的原理，2-4描述了某个神经元对应的原始的激活x通过减去mini-Batch内m个实例获得的m个激活x求得的均值E(x)并除以求得的方差Var(x)来进行转换，由此求出每一次小批量梯度下降激活的标准差。

等式5是中γ和β是所谓的批量归一化层的超参数。式5的输出具有β的平均值和γ的标准偏差。实际上，批量归一化层有助于优化算法来控制层的输出的均值和方差。

揭穿ICS的神秘面纱

Internal Covariate Shift是指我们训练网络时输入分布的变化。Batch Norm具有超参gamma和beta，用于调整激活的均值和方差。但是当这些超参数被训练时，它们也会发生变化，而BN导致激活分布或ICS的变化。如果它能阻止ICS，超参数gamma和beta没有任何意义。

为什么Batch Norm有效呢？

Ian Goodfellow，GANs的创始人，人工智能领域最重要的研究员之一，他在一个讲座中给出了可能的解释，在这一点上，我必须提醒你，除非我们通过具体证据支持，否则这只是猜测，不管它可能来自现代深度学习中的重量级人物之一。Goodfellow认为关键是BN的两个超参数。

 

让我们再次考虑超级简单的玩具网络：

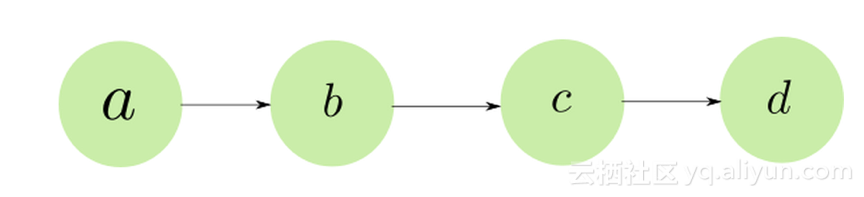
当我们对a的权重进行梯度更新时，我们只计算 frac {\ partial {L}} {\ partial {a}}，即损失函数相对于a的敏感度。但是，我们没有考虑到改变a的权重也会改变更多层的输出，如层b，c，d。

同样，由于使用这些算法的计算难度，这实际上归结为我们无法使用二阶或更高阶优化方法，梯度下降及其变型只适用于一阶。

深度神经网络具有高阶相互作用，这意味着除了损失函数之外，改变一个层的权重也可能影响其他层的统计。这些跨层在没有列入考虑的情况下交互会导致ICS。每次我们更新图层的权重时，它都有可能以不好的方式影响神经网络中图层的统计。

在这种情况下，收敛可能需要仔细初始化，调整超参数和更长的训练持续时间。但是，当我们在图层之间BN图层时，图层的统计信息仅受两个超参数gamma和beta的影响。

现在，我们的优化算法只必须仅两个超参数来控制任何层的统计数据，而不是前一层中的权重，这极大地加速了收敛，并且避免了初始化和超参数调整的需要。因此，Batch Norm更像是一个检查指向机制。

请注意，任意设置图层均值和标准差的能力也意味着如果充分地进行正确地训练，我们就可以恢复其原始分布。

激活前或激活后的BatchNorm

理论上在激活函数之前应用BN更好，但实际上已经发现在激活之后应用BN会产生更好的结果。在BN之后进行激活，BN无法完全控制进入下一层的输入的统计数据，因为BN的输出必须经过激活，在激活后应用BN却不是这种情况。

推论中的批量规范

在推理期间使用BN可能有点棘手,因为我们在推理期间可能并不总是有批处理。例如，在视频上实时运行对象检测器。一次处理一个帧，因此没有批处理。

我们需要计算批处理的均值hat {x}和方差sigma ^ 2 来生成BN的输出。在这种情况下，我们在训练期间保持均值和方差的滑动平均，然后在推理期间将这些值插入均值和方差,这很重要，也是大多数深度学习库采用的方法，可以开箱即用。

使用滑动平均的理由取决于大数定律。小批量的均值和方差是对真实均值和方差的非常粗糙的估计。批量估计称为批量统计，均值和方差的真实值（我们未知）称为人口统计。对于大量样本，批量统计数据往往会收敛于人口的统计数据，这就是为什么我们在训练时使用滑动平均。 由于我们的优化算法的小批量特性，它还有助于我们除去平均估计产生的噪声。

BNS是正则化器：

Batch Norm其实是一个正规化器，每个批次估计的均值和方差是真实均值的噪声版本，这在我们的最优搜索中注入了随机性，有助于正规化。

结论：

虽然Batch Norm现已成为深层架构的标准元素，但直到最近，研究一直致力于理解它是如何工作的。去年，我们还介绍了SELU或缩放指数线性单位激活函数，这些函数隐含地规范了通过它们的激活，这是通过BN明确完成的。

原文链接 

本文为云栖社区原创内容，未经允许不得转载。