摘要

摘要:本文提出了一种视差细化方法，通过对视差统计意义的探讨，直接细化赢者通吃视差图。根据基于分割的立体匹配的主要步骤，将参考图像过度分割为超像素，并通过改进的随机样本对每个超像素进行视差面拟合共识(RANSAC)。我们设计了一个两层优化来细化视差平面。在全局优化中，利用马尔可夫随机域(MRF)推理估计超像素点的平均视差，然后根据平均视差推导出遮挡处理的三维邻域系统。在局部优化中，采用贝叶斯推理和贝叶斯预测相结合的概率模型，隐式地实现了三维邻居间的二阶平滑。两层优化是一种纯视差细化方法，因为在细化过程中不需要立体图像对之间的相关信息。在Middlebury和KITTI数据集上的实验结果表明，该方法能够快速准确地进行立体匹配，有效地处理遮挡。由此可见，“匹配成本计算+视差细化”框架是在较低的计算成本下生成精确视差图的一种可能的解决方案。

 

 

1.相关工作

1.1MRF Stereo Methods

      马尔可夫随机场(MRF)立体视觉方法将匹配问题形式化为标签问题，其目标是优化测量标签质量的全局能量函数。传统的MRF立体方法[18]、[19]给每个像素分配一个一维离散视差标签。利用图割[20]、[21]、信念传播[22]、[23]、TRW[24]等优化方法，实现能量函数的最小化。基于图切割的扩展移动和交换移动[18]显示出良好的性能。这些移动可以同时更新所有像素的标签，因此优化很难被局部极小值捕获。一维标签立体声方法的缺点是建模高度倾斜的表面。三维标签立体方法[25][27]的提出，以建立更准确的模型。这些方法不仅可以对高度倾斜曲面进行建模，而且可以实现二阶平滑约束[25]、[28]、[29]。因此，它们通常比1D标签方法有更好的准确性。然而，像素级的全局优化使计算变得复杂。

   我们的方法在超像素层上执行一维标签MRF推理。由于超像素的数量远远小于图像中的像素数量，因此推理速度要快得多。与之前的工作不同，我们的工作是以superpixel的离散均值差作为标签。即使在高度倾斜的表面上，也能正确地估计出这种差异。

1.2 Segment-based Stereo Methods 

       基于分段的立体方法[30][32]假设场景结构为分段平面，差值映射的估计转化为为每个分段分配一个三维视差平面。首先，将参考图像分割成颜色均匀的区域。然后用已知的立体匹配方法计算初始视差图，通过对视差图的平面拟合生成候选视差平面。最后，利用图形切割和信念传播等全局优化方法，为每一段分配一个最优的平面标签。最终的结果取决于分割的质量。为了放宽路段约束，提出了若干改进措施。为了保证深度不连续只出现在段的边界上，过度分割是一种常见的解决方案。Bleyer等人提出了一个像素级的MRF公式，该公式包含了软分段约束。联合分割和视差计算[34]，[35]可以提高优化过程中的分割质量。但是这些方法有一个共同的缺点。一个段的finalplane标签是从候选标签集中分配的。有限集可能不包含正确的标记，在这种情况下，视差计划的估计是错误的，错误是无法纠正的。在wang和Zheng[36]的工作中，通过协同优化对总能量函数进行优化，并将其分解为局部优化的子目标能量函数和。优化过程是迭代的，局部优化可以修正虚规划。因此，该方法对初始拟合结果具有较强的鲁棒性。

     与以往的全局能量函数优化方法相比，该方法通过局部优化和隐式约束平滑来细化视差面。此外，视差细化方法不需要立体图像对之间的相关信息，因此可以在单一视图中进行处理。

 

2.OVERVIEW OF THE TWO LAYEROPTIMIZATION（两层优化的概述）

 

    我们提出了一个两层优化来细化WTAdisparity map。在全局优化层(第四节)，采用MRF优化算法对后向平行视差图进行估计。

3维邻域系统通过超像素的平均视差划分。在局部优化层(SectionV)中，RANSAC对超像素点拟合了倾斜平面A，并利用超像素点S的平均视差对拟合结果进行了约束。利用贝叶斯推理和贝叶斯预测的概率模型对初始倾斜视差图进行了改进。这两个优化层都在超像素级运行，具有很高的效率。

2.1. FRONT-PARALLEL DISPARITY MAP（前向-平行视差图）

我们使用全局MRF优化来估计一个前并行视差图。超像素被表示为图形节点。MRF优化的目的是最小化后续的能量。

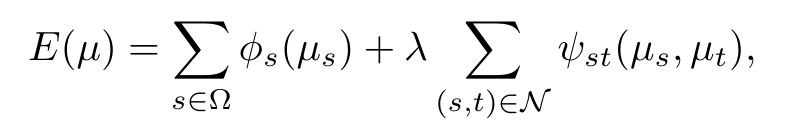
us是标签，在我们的例子中是超像素s的均值视差;n是超像素集合，N代表相邻超像素集合；g(us) 为数据项，f(us,ut)平滑项，l为平衡系数。与3D标签MRF相比，在超像素级优化1Dlabel是有效的(Section IV-B)。我们提出了一种新的基于视差分布(Section IV-A)的数据项，而不是基于左右图像之间的匹配成本或相似度度量。为了处理前-背景遮挡，由us推导出表示深度不连续的三维邻域系统(Section IV-C)。我们还研究了一个特殊的情况，证明1D标签的MRF公式不能模拟高裂纹表面(IV-D部分)。

A.视差分布的解释

   基于分段的立体视觉方法假设视差在一个分段内近似线性。在分段平面假设下，具有适当边界的平面的视差分布是均匀的。

考虑到超像素点的不规则边界形状，建立了超像素点内视差分布的数学模型超像素是正态分布。

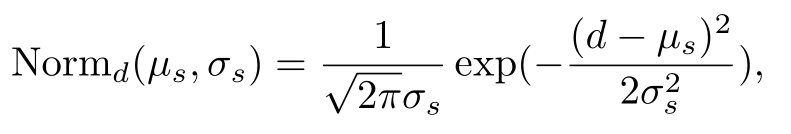
    d代表视差，us和ds分别代表超像素s的均值和方差。较高的ds表示较倾斜的表面，而对于前平行表面，ds 近似等于零。(2)的数据项基于视差分布直方图，如本节所述B

B.MRF Optimization

为了估计一个前向平行视差图，我们估计了超像素的超像素视差。front-parallel平面可以通过π=（0，0，us）获取。(2)的数据项和平滑项定义如下：

1）数据项：评估视差中心的置信度，超像素的视差分布是被分成直方图箱，我统计超像素视差落入直方图的数目，宽度为L。定义如下：

 

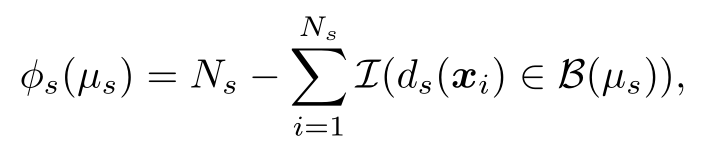
 Ns为在超像素的素数数目，us的取值为0，1l,2l......,而较低的数据项表示由于负号而较高的置信度，I是一个条件函数：

I表示是否落入Bin的直方图重。数据项的设计是基于投票的。

    落在同一个箱子里的观测次数越多，可信度越高。闭塞区域的wta差异存在噪声干扰，难以达成一致。因此，被遮挡区域的dataterm相对较高，标签以平滑项为主。

2）平滑项:平滑项使相邻超像素间的视差分布中心具有相似性，定义为：

Wst颜色相似度权重,定义为:

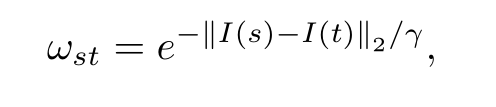
y是控制颜色权重的影响系数。I(S)为超像素的色彩平均值，E为下界截断值，L(s,t)相邻的超像素s和t是共享边界长度;T可以是一个度规或半度规，将在C部分定义。

C.3D邻域系统：

通过MRF优化估计的超像素平均视差提供了全局的场景信息。提出了表示深度不连续性的三维邻域系统：

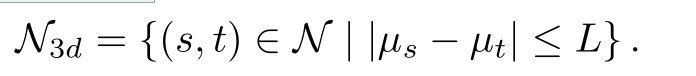
（s,t）为超像素对，如果他们均值视差不相似，那么他们的一范式大于L，那么他们不是相邻，因此，在N3d中可能存在的前-背景连接是切断的。这是遮挡处理的一个重要属性。E章节有更多的描述。

估计N3d的准确度，T是平滑项，通过定N3d ,T的定义如下：

其中τ> 2。Ts是一个半度量，它是非子模的，不能通过流行的扩展移动[18]来优化。

 

代码地址：https://github.com/TingmanYan/SDR