机器学习名词解释

1. 损失函数

损失函数是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

经验风险：一个损失函数的函数

结构风险：可简单理解为经验风险（一种损失函数的函数）+λ正则化项。

模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子：

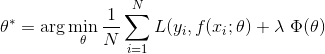
其中，前面的均值函数表示的是经验风险函数，L代表的是损失函数，后面的Φ是正则化项或者叫惩罚项，它可以是L1，也可以是L2，或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的θ值。常见的损失函数有:

n log对数损失函数（逻辑回归）

n 平方损失函数（最小二乘法）

n 指数损失函数（Adaboost）

n Hinge损失函数（SVM）

n 0-1损失

n 绝对值损失

正则化项或者叫惩罚项：

含义就是把整个模型中的所有权重w的绝对值加起来除以样本数量，其中是一个惩罚的权重，可以称为正则化系数或者惩罚系数，表示对惩罚的重视程度。如果很重视结构风险，即不希望结构风险太大，我们就加大，迫使整个损失函数向着权值w减小的方向移动，换句话说，w的值越多、越大，整个因子的值就越大，也就是越不简洁，刚才这种正则化因子叫做L1正则化项，常用的还有一种叫带有L2正则化项的损失函数。

将w做了平方后取加和。

2. 泛化能力

欠拟合和过拟合概念

欠拟合就是拟合效果非常差，比如一个一元二次方程，却用一元一次方程去拟合，这样的拟合效果肯定会很差。过拟合则是模型过于复杂，将训练数据拟合的十分到位，这样就容易拟合上许多噪音数据，这样对于训练数据他的误差会很小，但是对于预测数据即一些从来没有碰到过的数据，他的预测效果会特别差。对于未知数据的预测好坏通常叫做泛化能力。

如何判定模型是过拟合还是欠拟合

通常的办法是将训练数据分成2部分，一部分用来训练，让另一部分作为测试数据，检查他的泛化能力，如果泛化能力很差就是欠拟合，如果训练数据预测的很好，但是测试数据的精度却很差就是过拟合，我们可以通过学习曲线来将他可视化。

学习曲线

学习曲线其实就是把训练数据集取前i个样本（i 从1到训练数据样本总数）把模型的训练误差与预测误差都给表示出来，从而看误差的走势以及两者误差之间的关系，会发现最后误差一般都趋于稳定，如果模型较好，两者之间的差距也比较小。

3. 张量

想要了解张量(Tensor),首先需要对向量(Vector)有一个清晰的了解,向量通常都是这样一个箭头……用来表示一个既有幅度（magnitude）又有方向（direction）的物理量，比如重力、磁力或者一个粒子的速度。这个箭头的长度表示幅度，箭头的指向表示方向。

此外，向量还可以用来表示一个平面，表示方法就是让向量代表垂直于这个平面的方向（法线方向）。

这么看来，向量可以表示很多东西：表示力、速度甚至平面，不过仔细想想向量也只表示了幅度（magnitude）与方向（direction）两个要素而已。

还有很多物理量用向量是没法表示的（后面会提到），向量其实是一个更广泛的表示方法的特例。对的，你猜对了，这个更广泛的方法就是张量（Tensor）。为了更好的解释张量是什么，有两个概念需要先搞清楚：分量 (Components) 与基向量 (Basis Vectors）。张量是一种表示物理量的方式，这个方式就是用基向量与分量组合表示物理量（Combination of basis vector and component）。

张量是多维数组，目的是把向量、矩阵推向更高的维度。

4. 数据预处理之独热编码（One-Hot）

One-Hot编码，又称为一位有效编码，主要是采用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候只有一位有效。

One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后，每个整数值被表示为二进制向量，除了整数的索引之外，它都是零值，它被标记为1。

为什么使用one-hot编码来处理离散型特征?

在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。

而我们使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。

将离散型特征使用one-hot编码，确实会让特征之间的距离计算更加合理。

比如，有一个离散型特征，代表工作类型，该离散型特征，共有三个取值，不使用one-hot编码，其表示分别是x_1 = (1), x_2 = (2), x_3 = (3)。两个工作之间的距离是，(x_1, x_2) = 1, d(x_2, x_3) = 1, d(x_1, x_3) = 2。那么x_1和x_3工作之间就越不相似吗？显然这样的表示，计算出来的特征的距离是不合理。那如果使用one-hot编码，则得到x_1 = (1, 0, 0), x_2 = (0, 1, 0), x_3 = (0, 0, 1)，那么两个工作之间的距离就都是sqrt(2).即每两个工作之间的距离是一样的，显得更合理。

不需要使用one-hot编码来处理的情况

将离散型特征进行one-hot编码的作用，是为了让距离计算更合理，但如果特征是离散的，并且不用one-hot编码就可以很合理的计算出距离，那么就没必要进行one-hot编码。

比如，该离散特征共有1000个取值，我们分成两组，分别是400和600,两个小组之间的距离有合适的定义，组内的距离也有合适的定义，那就没必要用one-hot 编码。

离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。

5. 交叉熵

关于交叉熵在loss函数中使用的理解
交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。以前做一些分类问题的时候，没有过多的注意，直接调用现成的库，用起来也比较方便。当用到了交叉熵，发现自己对交叉熵的理解有些模糊，不够深入。遂花了几天的时间从头梳理了一下相关知识点，才算透彻的理解了，特地记录下来，以便日后查阅。

信息论
交叉熵是信息论中的一个概念，要想了解交叉熵的本质，需要先从最基本的概念讲起。

1 信息量
首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设XX是一个离散型随机变量，其取值集合为χχ,概率分布函数p(x)=Pr(X=x),x∈χp(x)=Pr(X=x),x∈χ,则定义事件X=x0X=x0的信息量为：

I(x0)=−log(p(x0))
I(x0)=−log(p(x0))

由于是概率所以p(x0)p(x0)的取值范围是[0,1][0,1],绘制为图形如下：

可见该函数符合我们对信息量的直觉
2 熵
考虑另一个问题，对于某个事件，有nn种可能性，每一种可能性都有一个概率p(xi)p(xi)
这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

序号   事件   概率p   信息量I
A   电脑正常开机   0.7   -log(p(A))=0.36
B   电脑无法开机   0.2   -log(p(B))=1.61
C   电脑爆炸了   0.1   -log(p(C))=2.30
注：文中的对数均为自然对数

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
H(X)=−∑i=1np(xi)log(p(xi))
H(X)=−∑i=1np(xi)log(p(xi))
其中n代表所有的n种可能性，所以上面的问题结果就是
H(X)===−[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))]0.7×0.36+0.2×1.61+0.1×2.300.804
H(X)=−[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))]=0.7×0.36+0.2×1.61+0.1×2.30=0.804
然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式：
H(X)==−∑i=1np(xi)log(p(xi))−p(x)log(p(x))−(1−p(x))log(1−p(x))
H(X)=−∑i=1np(xi)log(p(xi))=−p(x)log(p(x))−(1−p(x))log(1−p(x))
3 相对熵（KL散度）
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异

维基百科对相对熵的定义

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：
DKL(p||q)=∑i=1np(xi)log(p(xi)q(xi))(3.1)
(3.1)DKL(p||q)=∑i=1np(xi)log(p(xi)q(xi))

n为事件的所有可能性。
DKLDKL的值越小，表示q分布和p分布越接近
4 交叉熵
对式3.1变形可以得到：

DKL(p||q)==∑i=1np(xi)log(p(xi))−∑i=1np(xi)log(q(xi))−H(p(x))+[−∑i=1np(xi)log(q(xi))]
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：
H(p,q)=−∑i=1np(xi)log(q(xi))
H(p,q)=−∑i=1np(xi)log(q(xi))
在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||y^)DKL(y||y^)，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。