HMM 前向算法(Forward Algorithm)详细解释参考: http://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-1

http://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-2

http://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-3

http://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-4

后向算法（Backward Algorithm详细解释参考：http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-1

http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-2

http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-3

http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-4

http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-5

HMM模型参数解是HMM模型使用中的最复杂的一个问题。

HMM模型参数求解概述

HMM模型参数求解根据已知的条件可以分为两种情况。

第一种情况较为简单，就是我们已知D个长度为T的观测序列和对应的隐藏状态序列，即 $\left \{{(O_1,I_1),(O_2,I_2),...(O_D,I_D)} \right \}$ 是已知的，此时我们可以很容易的用最大似然来求解模型参数。

假设样本从隐藏状态 $q_i$ 转移到 $q_{j}$ 的频率计数是 $A_i_j$ ,那么状态转移矩阵求得为：

$\left A= [ \right a_{ij} ]$ ， $a_{ij}=\frac{A_{ij}}{\sum_{s=1}^{N}A_{is}}$

假设样本隐藏状态为 $q_j$ 且观测状态为 $v_k$ 的频率计数是 $B_j_k$ ,那么观测状态概率矩阵为：

$\left B= [ \right b_{j}(k) ]$ ， $b_{j}(k)=\frac{B_{jk}}{\sum_{s=1}^{M}B_{js}}$

假设所有样本中初始隐藏状态为 $q_i$ 的频率计数为C(i),那么初始概率分布为：

$\pi =\pi (i)=\frac{C(i)}{\sum_{s=1}^{N}C(s)}$

可见第一种情况下求解模型还是很简单的。但是在很多时候，我们无法得到HMM样本观察序列对应的隐藏序列，只有D个长度为T的观测序列，即是已知的，此时我们能不能求出合适的HMM模型参数呢？这就是我们的第二种情况，也是我们本文要讨论的重点。它的解法最常用的是鲍姆-韦尔奇算法，其实就是基于EM算法的求解，只不过鲍姆-韦尔奇算法出现的时代，EM算法还没有被抽象出来，所以我们本文还是说鲍姆-韦尔奇(Baun-Welch)算法。

Baum-Welch算法是为了解决HMM的参数估计问题而提出的，而且是没有标注也就是HMM的状态序列未知的参数估计问题。具体来说，就是已知观测序列O=(o1,o2,...,oT)，估计模型参数λ=(A,B,π)，使得在该模型下观测序列概率P(O|λ)最大。由于状态序列未知，因此这可以看做是一个含有隐变量的参数估计问题，解决这一问题的经典算法就是EM算法。Baum-Welch算法就是EM算法在隐马尔科夫模型学习中的具体体现。下面简单叙述一下该算法。

Baun-Welch算法原理

鲍姆-韦尔奇算法原理既然使用的就是EM算法的原理，那么我们需要在E步求出联合分布 $P\left (O, \right I\mid\lambda )$ 基于条件概率 $P\left (O, \right I\mid\lamb\lamb\overline{\lambda } )$ 的期望，其中 $\widetilde{\lambda }$ 为当前的模型参数，然后再M步最大化这个期望，得到更新的模型参数λ。接着不停的进行EM迭代，直到模型参数的值收敛为止。

　首先来看看E步，当前模型参数为 $\overline{ \lambda }$ , 联合分布 $P(O,I|\lambda )$ 基于条件概率 $P(I|O,\overline{\lambda })$ 的期望表达式为：

在M步，我们极大化上式，然后得到更新后的模型参数如下：

通过不断的E步和M步的迭代，直到收敛。下面我们来看看鲍姆-韦尔奇算法的推导过程。

Baun-Welch算法的推导

我们的训练数据为 $\left \{ {(O_1,I_1),(O_2,I_2),...(O_D,I_D)} \}$ ，其中任意一个观测序列 $O_d=\{ {o^{(d)}_1,o^{(d)}_2,...o^{(d)}_T} \}$ ,其对应的未知的隐藏状态序列表示为： $I_d=\{ {i^{(d)}_1,i^{(d)}_2,...i^{(d)}_T} \}$ .

首先看鲍姆-韦尔奇算法的E步，我们需要先计算联合分布 $P(O,I|\lambda )$ 的表达式如下:

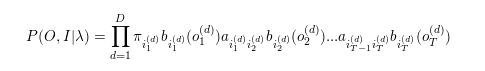
我们的E步得到的期望表达式为：

$\small L(\lambda, \overline{\lambda}) = \sum\limits_{I}P(I|O,\overline{\lambda})logP(O,I|\lambda)$

在M步我们要极大化上式。由于 $P(I|O,\overline{\lambda})=\frac{P(I,O|\overline{\lambda})}{P(O|\overline{\lambda})}$ ,而 $P(O|\overline{\lambda})$ 是常数，因此我们要极大化的式子等价于：

$\small \overline{\lambda} = arg\;\max_{\lambda}\sum\limits_{I}P(O,I|\overline{\lambda})logP(O,I|\lambda)$

我们将上面 $P(O,I|\lambda )$ 的表达式带入我们的极大化式子，得到的表达式如下：

$\small \overline{\lambda} = arg\;\max_{\lambda}\sum\limits_{d=1}^D\sum\limits_{I}P(O,I|\overline{\lambda})(log\pi_{i_1} + \sum\limits_{t=1}^{T-1}log\;a_{i_t}a_{i_{t+1}} + \sum\limits_{t=1}^Tb_{i_t}(o_t))$

我们的隐藏模型参数 $\lambda =(A,B,\Pi )$ ,因此下面我们只需要对上式分别对A,B,Π求导即可得到我们更新的模型参数 $\overline{\lambda }$ .

首先我们看看对模型参数Π的求导。由于Π只在上式中括号里的第一部分出现，因此我们对于Π的极大化式子为：

$\small \overline{\pi_i} = arg\;\max_{\pi_{i_1}} \sum\limits_{d=1}^D\sum\limits_{I}P(O,I|\overline{\lambda})log\pi_{i_1} = arg\;\max_{\pi_{i}} \sum\limits_{d=1}^D\sum\limits_{i=1}^NP(O,i_1^{(d)} =i|\overline{\lambda})log\pi_{i}$

由于 $\pi_i$ 还满足 $\sum_{i=1}^{N}\pi_i=1$ ，因此根据拉格朗日子乘法，我们得到要极大化的拉格朗日函数为：

$\small arg\;\max_{\pi_{i}}\sum\limits_{d=1}^D\sum\limits_{i=1}^NP(O,i_1^{(d)} =i|\overline{\lambda})log\pi_{i} + \gamma(\sum\limits_{i=1}^N\pi_i -1)$

其中， $\gamma$ 为拉格朗日系数。上式对 $\pi_i$ 求偏导数并令结果为0，我们得到：

$\small \sum\limits_{d=1}^DP(O,i_1^{(d)} =i|\overline{\lambda}) + \gamma\pi_i = 0$

令i分别等于从1到N，从上式可以得到N个式子，对这N个式子求和可得：

$\small \sum\limits_{d=1}^DP(O|\overline{\lambda}) + \gamma = 0$

从上两式消去,得到的表达式为：

$\small \pi_i =\frac{\sum\limits_{d=1}^DP(O,i_1^{(d)} =i|\overline{\lambda})}{\sum\limits_{d=1}^DP(O|\overline{\lambda})} = \frac{\sum\limits_{d=1}^DP(O,i_1^{(d)} =i|\overline{\lambda})}{DP(O|\overline{\lambda})} = \frac{\sum\limits_{d=1}^DP(i_1^{(d)} =i|O, \overline{\lambda})}{D} = \frac{\sum\limits_{d=1}^DP(i_1^{(d)} =i|O^{(d)}, \overline{\lambda})}{D}$

由前向概率的定义可得：

$\small P(i_1^{(d)} =i|O^{(d)}, \overline{\lambda}) = \gamma_1^{(d)}(i)$

因此最终我们在M步的迭代公式为：

$\small \pi_i = \frac{\sum\limits_{d=1}^D\gamma_1^{(d)}(i)}{D}$

现在我们来看看A的迭代公式求法。方法和Π的类似。由于A只在最大化函数式中括号里的第二部分出现，而这部分式子可以整理为：

$\small \sum\limits_{d=1}^D\sum\limits_{I}\sum\limits_{t=1}^{T-1}P(O,I|\overline{\lambda})log\;a_{i_t}a_{i_{t+1}} = \sum\limits_{d=1}^D\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}P(O,i_t^{(d)} = i, i_{t+1}^{(d)} = j|\overline{\lambda})log\;a_{ij}$

由于 $a_i_j$ 还满足 $\sum^{N}_{j=1}a_i_j=1$ 。和求解 $\pi _i$ 类似，我们可以用拉格朗日子乘法并对 $a_i_j$ 求导，并令结果为0，可以得到 $a_i_j$ 的迭代表达式为：

$a_{ij} = \frac{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T-1}P(O^{(d)}, i_t^{(d)} = i, i_{t+1}^{(d)} = j|\overline{\lambda})}{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T-1}P(O^{(d)}, i_t^{(d)} = i|\overline{\lambda})}$

给定模型λ和观测序列O,在时刻t处于状态 $q_i$ ，且时刻t+1处于状态 $q_j$ 的概率记为:

$\xi_t(i,j) = P(i_t = q_i, i_{t+1}=q_j | O,\lambda) = \frac{ P(i_t = q_i, i_{t+1}=q_j , O|\lambda)}{P(O|\lambda)}$

而 $P(i_t = q_i, i_{t+1}=q_j , O|\lambda)$ 可以由前向后向概率来表示为:

$P(i_t = q_i, i_{t+1}=q_j , O|\lambda) = \alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$

从而最终我们得到 $\xi_t(i,j)$ 的表达式如下：

$\xi_t(i,j) = \frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum\limits_{r=1}^N\sum\limits_{s=1}^N\alpha_t(r)a_{rs}b_s(o_{t+1})\beta_{t+1}(s)}$

因此可得 $b_{j}(o_t)$ 表达式：

$b_{j}(k) = \frac{\sum\limits_{d=1}^D\sum\limits_{t=1, o_t^{(d)}=v_k}^{T}\gamma_t^{(d)}(i)}{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T}\gamma_t^{(d)}(i)}$

有了 $\pi_i, a_{ij},b_{j}(k)$ 的迭代公式，我们就可以迭代求解HMM模型参数了。

Baun-Welch算法流程总结

这里我们概括总结下鲍姆-韦尔奇算法的流程。

输入： D个观测序列样本 $\{(O_1), (O_2), ...(O_D)\}$

输出：HMM模型参数

1)随机初始化所有的 $\pi_i, a_{ij},b_{j}(k)$

2) 对于每个样本 $d = 1,2,...D$ ，用前向后向算法计算 $\gamma_t^{(d)}(i), \xi_t^{(d)}(i,j), t =1,2...T$

3) 更新模型参数：

$\pi_i = \frac{\sum\limits_{d=1}^D\gamma_1^{(d)}(i)}{D}$

$a_{ij} = \frac{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T-1}\xi_t^{(d)}(i,j)}{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T-1}\gamma_t^{(d)}(i)}$

$b_{j}(k) = \frac{\sum\limits_{d=1}^D\sum\limits_{t=1, o_t^{(d)}=v_k}^{T}\gamma_t^{(d)}(i)}{\sum\limits_{d=1}^D\sum\limits_{t=1}^{T}\gamma_t^{(d)}(i)}$

4) 如果 $\pi_i, a_{ij},b_{j}(k)$ 的值已经收敛，则算法结束，否则回到第2）步继续迭代。

　　　　以上就是Baun-Welch算法的整个过程。