今天碰到了这样一个情况, 使我又去翻阅了原来课本, 在Pthon中如果输入下面这段程序:
print(sys.float_info.max - 1.0)
print(sys.float_info.max)
结果如下:
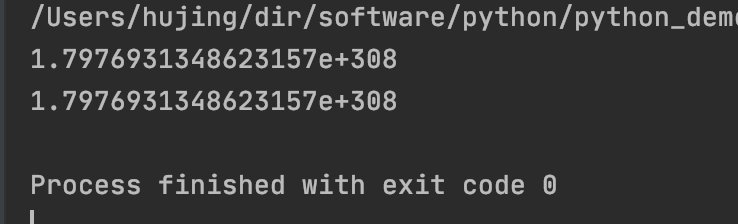
结果发现, 这数字根本没有变化. 本来这没什么, 看这数字, 10的308次方, 也就是说, 减去的1是在308位之后了, 这里没有变化很正常嘛.
但是下面的现象就不能解释了:
a = sys.float_info.max - 1.0
b = sys.float_info.max
print(a == b)
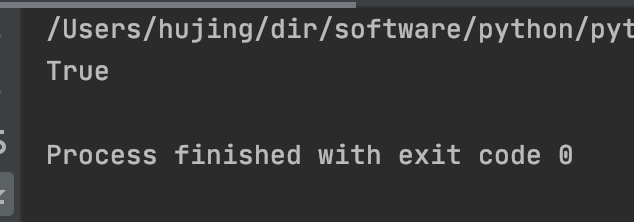
结果显示, 两个数字完全一样, 这这这, 不行, 我得去回顾一下浮点数的表示.
小数的存储
如果要存储小数, 一般来说又两种保存方式.
1. 固定位数
将小数进行放大, 进行整数化, 然后保存整数. 如果固定知道是两位小数的话, 那么将小数乘以100, 就得到了一个对应的整数.
这种方式的前提是需要确切的知道小数的位数, 但是好在精度高, 在运算的时候不会造成误差. 比较适合保存金额等.
同时, 因为固定了位数, 不管你有没有小数, 都需要占用位数, 所以就导致在位数一定的情况下, 能够存储的最大值变小了.
2. 浮点数
但是, 在正常使用的时候, 通常是不知道小数的确切位数, 怎么办呢? 科学记数法想必都不陌生 a*b^n, 浮点数其实就是根据它来, 其存储结构如下(64位):
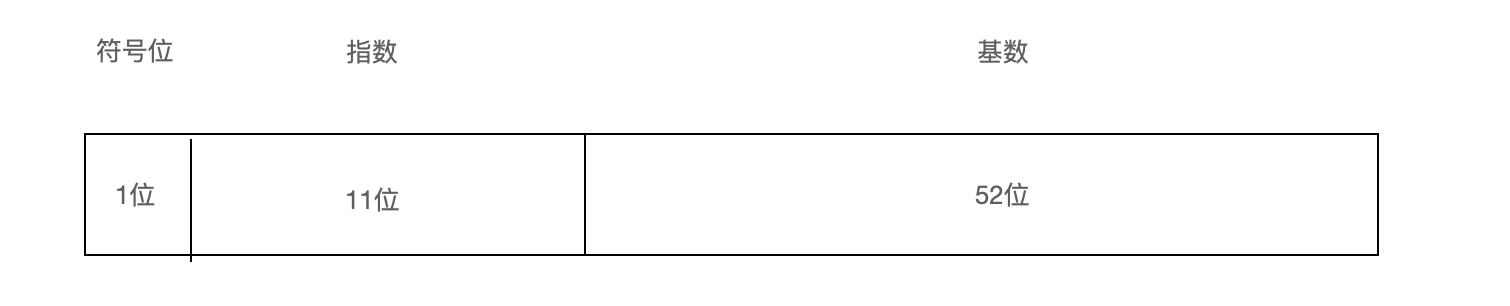
- 符号位: 标识数字的正负
- 指数: 2^n. 其中这个指数是分正负的哦, 也可以理解为小数点偏移量.
- 基数: 规定基数是一个大于等于1, 小于2的数字, 也就是基数前面有一个隐含的默认1, 基数标识小数点后面的内容
那么问题来了, 基数隐含了一个默认的1, 那浮点数如何表示0呢?
- 当指数为全0的时候, 若基数为全0, 则表示0.
- 当指数为全1的时候, 表示无穷大.
同时, 因为位数的限制, 并不能保存无穷大的数字, 包括无限小数, 就比如0.1
简单回顾一下, 足够解释今天的奇怪现象了.
再看
回顾了小数的保存之后, 再来回看之前的, 为什么浮点数最大值, 减去1之后, 本身没有任何变化呢?
要回答这个问题, 还需要知道两个浮点数在计算机中是如何进行计算的. 在两个浮点数进行运算的时候, 要先将指数部分保持一致, 然后再进行相应的运算, 也就是说:
1.0*10^4 + 1.0*10^2 要转换成: 1.0*10^4 + 0.01*10^4
如此, 上面的最大值, 其指数部分为 2^1023. 所以, 要将浮点数1.0进行转换, 而这个数字要想转换成相同指数的话, 其基数部分就要后移1023位, 导致溢出, 就变成0了. 所以就相当于和0做运算, 其结果不变.
如此说来, 浮点数的指数在进行转换的时候, 岂不是很容易丢失精度? 还真是, 看这个例子:
a = 1.0
b = 0.12345678
c = 0.11111111s = 0.0
s += a
s += b
s += cprint(s)s += 10000000.0
s += -10000000.0
print(s)
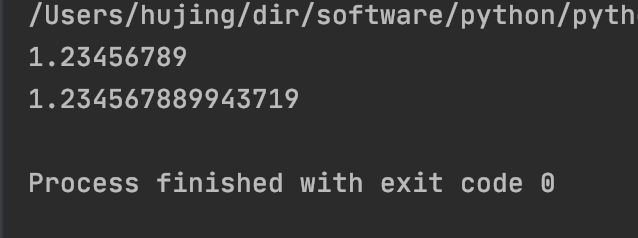
可以看到, 在开始数字之间相差不大的时候, 结果还是正确的. 但是之后只是对同一个数字做了一次加减, 就导致发生其精度丢失了. 其原因同样是因为在计算中对指数部分统一导致的.
为了验证我的猜想, 只要将计算顺序修改, 当 s 变量还没有小数部分, 不至于丢失精度的时候进行大数的运算:
a = 1.0
b = 0.12345678
c = 0.11111111s = 0.0
s += a
s += 10000000.0
s += -10000000.0
s += b
s += cprint(s)
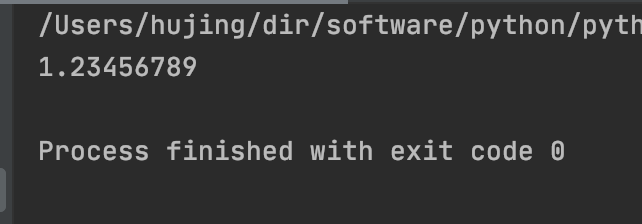
这时, 计算结果印证了之前的讨论. 如此说来, 小数在两个相差很多的数字之间进行运算的时候, 也容易导致丢失精度.
同时, 因为浮点数能表示的范围比整数要大, 在转整数的时候, 也可能会造成丢失.
最终搞懂了这个看似奇怪的现象, 唉, 基础还是不够啊.


















覆盖优化 - 附代码)
