注意力机制--转载自我的学生隆兴写的博客

原文链接为：https://a-egoist.com/posts/a44b8419/，学生自己搭建的博客，点赞！

1 Attention

1.1 什么是 Attention

灵长类动物的视觉系统中的视神经接受了大量的感官输入。在检查视觉场景时，我们的视觉神经系统大约每秒收到 $10^8$ 位的信息，这远远超过了大脑能够完全处理的水平。但是，并非所有刺激的影响都是相等的。意识的聚集和专注使灵长类动物能够在复杂的视觉环境中将注意力引向感兴趣的物体，例如猎物和天敌。

在心理学框架中，人类根据随意(有意识)线索和不随意(无意识)线索选择注意点。下面两张图展现了在随意线索和不随意线索的影响下，眼的注意力集中的位置。
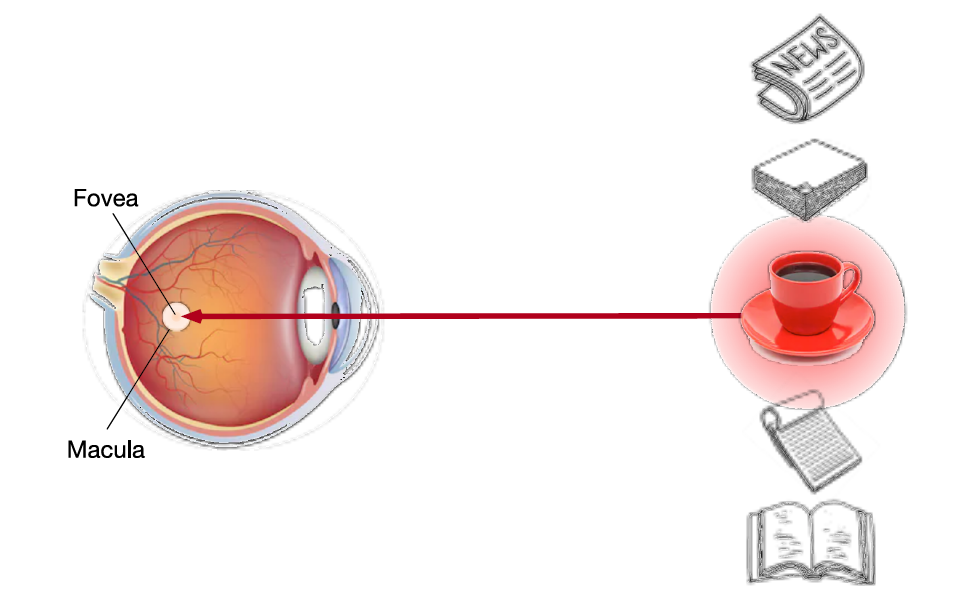
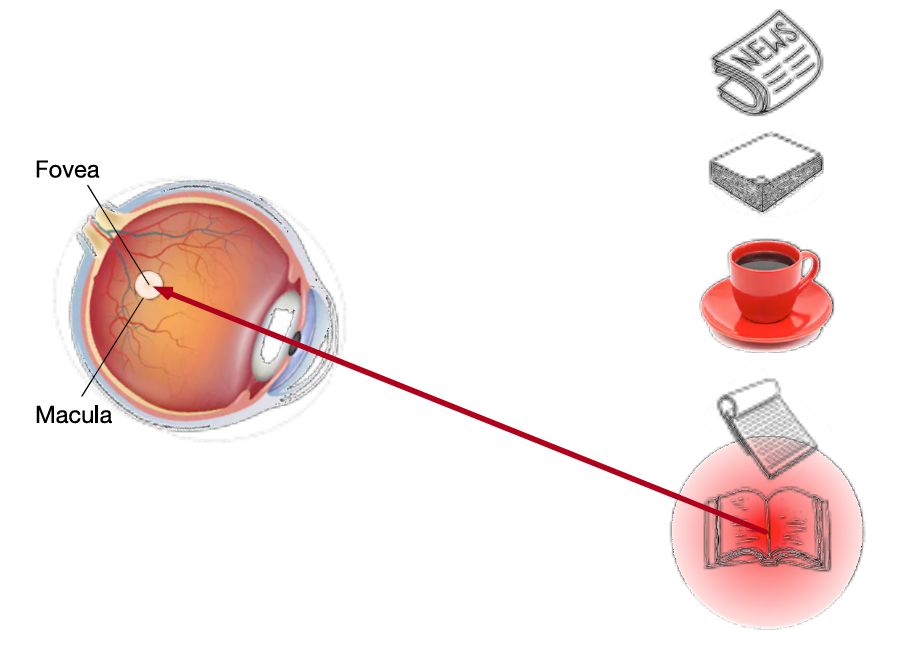
在这里插入图片描述

卷积、全连接层、池化层基本上都只考虑不随意线索，注意力机制则显式地考虑随意线索。

在注意力机制中，定义以下三点：

随意线索被称为查询(query)
每个输入是一个不随意线索(key)和值(value)的 pair
通过注意力池化层来有偏向性的选择某些输入
- 一般写作 $f(x)=∑iα(x,xi)yif(x)=\sum_i\alpha(x,x_i)y_i$ ，其中 $α(x,xi)\alpha(x,x_i)$ 表示注意力权重

1.2 非参注意力池化层

早在 60 年代就出现了非参数的注意力机制。假设给定数据 $(xi,yi),i=1,…,n(x_i,y_i),i=1,\dots,n$ ，其中 $x_i$ 表示 key， $y_i$ 表示 value，要想根据 query 将数据进行池化

最简单的方案——平均池化：
$f(x)=1n∑iyi(1)f(x)=\frac{1}{n}\sum_iy_i\tag{1}$

无论输入的 $x$ 是什么，每次都返回所有 value 的均值。

Nadaraya-Waston 核回归：
$f(x)=∑i=1nK(x−xi)∑j=1nK(x−xj)yi(2)f(x)=\sum_{i=1}^{n} \frac{K\left(x-x_{i}\right)}{\sum_{j=1}^{n} K\left(x-x_{j}\right)} y_{i}\tag{2}$
其中， $f(⋅)f(\cdot)$ 中的 $x$ 表示 query， $K(⋅)K(\cdot)$ 表示核函数，用于衡量 query $x$ 和 key $x_i$ 之间的距离。这一个方法可以类比于 K-Nearest Neighbor，对于一个 query 函数的输出跟倾向于与其最相关的 value，而这个相关性则通过 query 和 key 共同计算出来。

若公式 $(2)$ 中的 $K(⋅)K(\cdot)$ 使用的是高斯核： $K(μ)=12πexp⁡(−μ22)K(\mu)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{\mu^2}{2})$ ，那么可得：
$f(x)=∑i=1nexp⁡(−12(x−xi)2)∑j=1nexp⁡(−12(x−xj)2)yi=∑i=1nsoftmax⁡(−12(x−xi)2)yi(3)\begin{aligned} f(x) &=\sum_{i=1}^{n} \frac{\exp \left(-\frac{1}{2}\left(x-x_{i}\right)^{2}\right)}{\sum_{j=1}^{n} \exp \left(-\frac{1}{2}\left(x-x_{j}\right)^{2}\right)} y_{i} \\ &=\sum_{i=1}^{n} \operatorname{softmax}\left(-\frac{1}{2}\left(x-x_{i}\right)^{2}\right) y_{i} \end{aligned}\tag{3}$

1.3 参数化的注意力机制

在公式 $(3)$ 的基础上引入可以学习的参数 $w$ ：
$f(x)=∑i=1nsoftmax⁡(−12((x−xi)w)2)yi(4)f(x)=\sum_{i=1}^{n} \operatorname{softmax}\left(-\frac{1}{2}\left(\left(x-x_{i}\right) w\right)^{2}\right) y_{i}\tag{4}$

1.4 注意力分数

由公式 $(3)$ 可得：
$f(x)=∑iα(x,xi)yi=∑i=1nsoftmax⁡(−12(x−xi)2)yi(5)f(x)=\sum_{i} \alpha\left(x, x_{i}\right) y_{i}=\sum_{i=1}^{n} \operatorname{softmax}\left(-\frac{1}{2}\left(x-x_{i}\right)^{2}\right) y_{i}\tag{5}$
其中 $α(⋅)\alpha(\cdot)$ 表示注意力权重，根据输入的 query 和 key 来计算当前 value 的权重； $−12(x−xi)2-\frac{1}{2}\left(x-x_{i}\right)^{2}$ 表示的就是注意力分数。

计算注意力的过程如图所示：

首先根据输入的 query，来计算 query 和 key 之间的 attention score，然后将 score 进行一次 $softmax⁡\operatorname{softmax}$ 得到 attention weight，attention weight 和对应的 value 做乘法再求和得到最后的输出。

拓展到高纬度

假设 query $q∈Rq\mathbf{q} \in \mathbb{R}^{q}$ ， $m$ 对 key-value $(k1,v1),…,(\mathbf{k}_{1}, \mathbf{v}_{1}),\dots,$ 这里 $ki∈Rk\mathbf{k}_{i} \in \mathbb{R}^{k}$ ， $vi∈Rv\mathbf{v}_{i} \in \mathbb{R}^{v}$

注意力池化层：
$f(q,(k1,v1),…,(km,vm))=∑i=1mα(q,ki)vi∈Rvα(q,ki)=softmax⁡(a(q,ki))=exp⁡(a(q,ki))∑j=1mexp⁡(a(q,kj))∈R(6)\begin{array}{c} f\left(\mathbf{q},\left(\mathbf{k}_{1}, \mathbf{v}_{1}\right), \ldots,\left(\mathbf{k}_{m}, \mathbf{v}_{m}\right)\right)=\sum_{i=1}^{m} \alpha\left(\mathbf{q}, \mathbf{k}_{i}\right) \mathbf{v}_{i} \in \mathbb{R}^{v} \\ \alpha\left(\mathbf{q}, \mathbf{k}_{i}\right)=\operatorname{softmax}\left(a\left(\mathbf{q}, \mathbf{k}_{i}\right)\right)=\frac{\exp \left(a\left(\mathbf{q}, \mathbf{k}_{i}\right)\right)}{\sum_{j=1}^{m} \exp \left(a\left(\mathbf{q}, \mathbf{k}_{j}\right)\right)} \in \mathbb{R} \end{array}\tag{6}$
其中 $softmax⁡(⋅)\operatorname{softmax}(\cdot)$ 中的参数 $a(q,ki)a(\mathbf{q},\mathbf{k}_i)$ 表示注意力分数。

从公式 $(6)$ 可以看出，我们应该关注 $a(⋅)a(\cdot)$ 怎么设计，接下来介绍两种思路。

1.4.1 Additive Attention

可学参数： $Wk∈Rh×k,Wq∈Rh×q,v∈Rh\mathbf{W}_{k}\in\mathbb{R}^{h\times k},\mathbf{W}_{q}\in\mathbb{R}^{h\times q},\mathbf{v}\in \mathbb{R}^{h}$
$a(k,q)=vTtanh⁡(Wkk+Wqq)a(\mathbf{k}, \mathbf{q})=\mathbf{v}^{T} \tanh \left(\mathbf{W}_{k} \mathbf{k}+\mathbf{W}_{q} \mathbf{q}\right)$
其中 $tanh⁡(⋅)\operatorname{tanh}(\cdot)$ 表示 tanh 激活函数。等价于将 query 和 key 合并起来后放到一个隐藏层大小为 h 输出大小为 1 的单隐藏层 MLP

该方法中 query、key 和 value 的长度可以不一样。

1.4.2 Scaled Dot-Product Attention

如果 query 和 key 都是同样的长度 $q,ki∈Rd\mathbf{q},\mathbf{k}_i\in\mathbb{R}^d$ ，那么可以：
$a(q,ki)=⟨q,ki⟩/da\left(\mathbf{q}, \mathbf{k}_i\right)=\left\langle\mathbf{q}, \mathbf{k}_i\right\rangle/\sqrt{d}$
向量化版本

query $Q∈Rn×d\mathbf{Q} \in \mathbb{R}^{n \times d}$ , key $K∈Rm×d\mathbf{K} \in \mathbb{R}^{m \times d}$ , value $V∈Rm×v\mathbf{V} \in \mathbb{R}^{m \times v}$

attention score: $a(Q,K)=QKT/d∈Rn×ma(\mathbf{Q}, \mathbf{K})=\mathbf{Q K}^{T} / \sqrt{d} \in \mathbb{R}^{n \times m}$

attention pooling: $f=softmax⁡(a(Q,K))V∈Rn×vf=\operatorname{softmax}(a(\mathbf{Q}, \mathbf{K})) \mathbf{V} \in \mathbb{R}^{n \times v}$

2 Self-attention

2.1 什么是 Self-attention

下面三幅图展示了 CNN、RNN 和 self-attention 如何处理一个序列的输入。

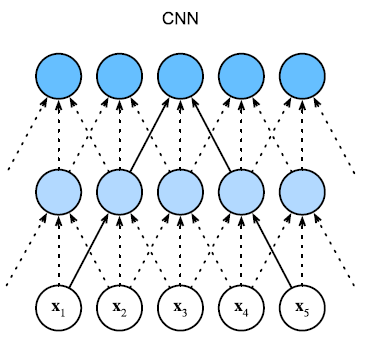
CNN 会考虑当前输入和其前面的 n 个输入以及后面 n 个输入的关系。

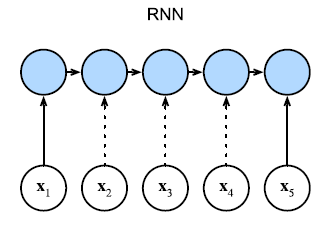
RNN 会考虑当前输入和其前面的所有输入的关系。

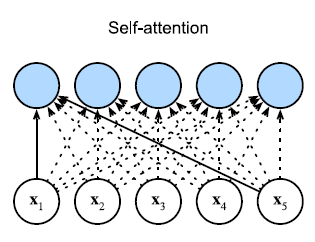
Self-attention 会考虑当前输入和全局输入的关系。

总的来说，Self-attention 可以表述为：给定序列 $x1,…,xn,∀xi∈Rd\mathbf{x}_{1},\ldots,\mathbf{x}_{n},\forall \mathbf{x}_{i}\in\mathbb{R}^{d}$ ，自注意力池化层将 $xi\mathbf{x}_{i}$ 当做 key, value, query 来对序列抽取特征得到 $y1,…,yn\mathbf{y}_{1},\ldots,\mathbf{y}_{n}$ ，这里
$yi=f(xi,(x1,x1),…,(xn,xn))∈Rd\mathbf{y}_{i}=f\left(\mathbf{x}_{i},\left(\mathbf{x}_{1}, \mathbf{x}_{1}\right), \ldots,\left(\mathbf{x}_{n}, \mathbf{x}_{n}\right)\right) \in \mathbb{R}^{d}$

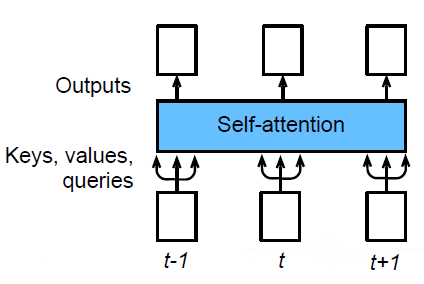
2.2 Self-attention 怎样运作

对于每一个输入 $a^i$ 在考虑其与全局的关联性之后得到 $b^i$

如何计算 $a^1$ 和 $a^2,a^3,a^4$ 的关联性？在 1.4 节中介绍的注意力分数计算方法就是用于计算 query 和 key 之间关联性的方法。即常用的 Dot-product attention 和 Additive attention。

计算 $a^1$ 和 $a^2,a^3,a^4$ 的关联性

对于输入 $a^i$ 将其分别左乘上矩阵 $W^q,W^k,W^v$ 得到 $q^i,k^i,v^i$ ，然后利用 $q^i,k^j$ 计算 $a^i,a^j$ 之间的关联性，计算结果为 attention score，将 attention score 放入激活函数后得到 attention weight，attention weight 乘上 $v^j$ 再求和可得到 $b^i$ ，即 $a^i$ 对应的输出。

矩阵化

通过上面的几张图可以看出，虽然 Self-attention 中间做了很多复杂的工作，但是在 Self-attention 中需要学习的参数只有 $W^q,W^k,W^v$ ，其他的参数都是预先设定好的。

2.3 Multi-head Self-attention

在 Self-attention 中，我们使用 query 去需要相关的 key，但是相关有很多种不同的定义，不同的定义与不同的 query 绑定，即同一个输入需要有多个 query。

在上图中，在 Self-attention 的基础上对于每个 $q^i,k^i,v^i$ 其左乘上一个矩阵可以得到 $q^{i,1},q^{i,2},k^{i,1},k^{i,2},v^{i,1},v^{i,2}$ ，然后按照 Self-attention 中相同的计算方式可以得到 $b^{i,1},b^{i,2}$ 。

然后将得到的 $b^{i,1},b^{i,2}$ 接起来左乘一个矩阵就可以得到 Multi-head Self-attention 的输出 $b^i$ 。

2.4 Position Encoding

因为 Self-attention 考虑的是全局的信息，而且即便输入的顺序改变了，也不会影响输出的结果。但是在实际的应用中，很多时候需要考虑位置信息，例如一个 sequence。因此，为了让 Self-attention 能够考虑到位置信息，为每个输入加上一个 position encoding。

其中 $e^i$ 表示在每个输入上增加的 position encoding 信息，对于每个 $a^i$ 都有一个专属的 $e^i$ 与之对应。 $e^i$ 产生的方式有很多种，在论文 Learning to Encode Position for Transformer with Continuous Dynamical Model 中提出并比较了 position encoding。

2.5 Self-attention for Image

对于一张 shape = (5, 10, 3) 的 RGB 图片，可以将其看成一个 vector set，其中的每一个 pixel 都可以看成一个 vector (r, g, b)，然后就可以将其放入 Self-attention 模型进行计算。

3 Self-attention v.s. CNN

CNN 和 Self-attention 都可以考虑一定范围内的信息，但是 CNN 只能够考虑到感受野内的信息，而 Self-attention 能够考虑到全局的信息。因此可以把 CNN 看做 Self-attention 的简化版本，Self-attention 看做 CNN 的复杂化版本。

从集合的角度来看，CNN 可以看做是 Self-attention 的子集。在论文 ON THE RELATIONSHIP BETWEEN SELF-ATTENTION AND CONVOLUTIONAL LAYERS 中详细介绍了 Self-attention 和 CNN 的关系。

从下图(出自论文 AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE)中的数据可以看出，利用较小的数据量训练时，CNN 的效果优于 Self-attention，但是随着数据量的增大，Self-attention 的效果越来越好，在数据量达到 300 Million 的时候 Self-attention 的效果会优于 CNN。

4 Summary

本篇博客对 attention 做了一个基本介绍，然后又介绍了 attention 最常用的一种实现 Self-attention，Self-attention 在 Transformer 和 BERT 中有着举足轻重的地位。我最开始学习 attention 的目的，是为了了解其在 computer vision 方向的应用，所以在之后的博客中我会更加详细的介绍目前 attention 在 computer vision 方向的应用以及遇到的问题。