1 什么是编辑距离
在计算文本的相似性时,经常会用到编辑距离(Levenshtein距离),其指两个字符串之间,由一个字符串转成另一个所需的最少编辑操作次数。在字符串形式上来说,编辑距离越小,那么两个文本的相似性越大,暂时不考虑语义上的问题。其中,编辑操作包括以下三种:
插入:将一个字符插入某个字符串
删除:将字符串中的某个字符删除
替换:将字符串中的某个字符串替换为另一个字符
为了更好地说明编辑距离的概念,我们看看一个例子,将字符串“batyu”变为“beauty”,编辑距离是多少呢?分析步骤如下:
将batyu插入字符e有:beatyu
将beatyu删除字符u有:beaty
将beaty插入字符u有:beauty
所以,字符串“batyu”与字符串“beauty”之间的编辑距离为:3.
2 数学化
先抛开具体编程语言实现,我们简单地分析一下如何计算两个字符串之间的编辑距离
当两个字符串都为空串的时候,那么编辑距离就是0
当其中一个字符串为空串时,那么编辑距离为另一个非空字符串的长度
当两个字符串A,B均为非空时(假设长度分别为i,j),那么有如下三种情况,我们取这三种情况的最小值即可:
1). 已知字符串A中长为 i - 1(从字符串首开始,以下描述字符串长默认此种描述)和字符串B长为j的编辑距离,那么在此基础上加1即可
2).长度分别为i,h和j-1的编辑距离已知,那么加1即可
3).长度分别为i-1和j-1的编辑距离已知,这个时候需要考虑两种情况,若第i个字符和第j个字符不同,那么加1即可,如果相同,那么就不需要加1.
从上面的描述,很明显可以发现是动态规划的思想。
我们将上面的叙述数学化,则有:求长度为m和n的字符A、B串编辑距离,即函数:edit(i,j),它表示第一个长度为i(从字符首开始)的字符串与第二个长度为j的字符串之间的编辑距离。动态规划表达式则有如下写法,假设i,j表示字符串A,B的字串长度:
if i==0 且 j==0,edit(i,j)=0
if (i==0 且 j>0) 或者(i>0 且j ==0),edit(i,j)=i + j
if i>= 1 且 j >= i, edit(i, j) = min(edit(i-1,j) + 1, edit(i, j-1) + 1, edit(i-1,j-1) + d(i,j);当第一个字符串的第i个字符不等于第二个字符串第j个字符时,d(i,j)=1,否则为0
字符串“batyu”与字符串“beauty”之间的编辑距离矩阵则有如下表示:
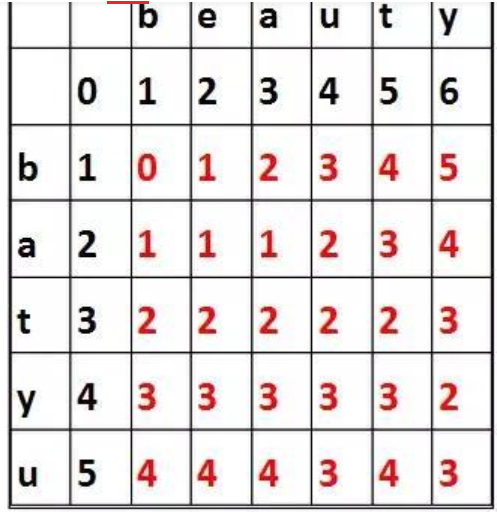
最终的编辑距离即为edit(m,n)。
3 编程实现
有了上面的思路,使用Python去实现计算两个字符串的编辑距离就简单多了。
def test(s1,s2):
edit = [[i+j for j in range(len(s2)+1)] for i in range(len(s1)+1)]
for i in range(1,len(s1)+1):
for j in range(1,len(s2)+1):
if s1[i-1]==s2[j-1]:
d=0
else:
d=1
edit[i][j] = min(edit[i-1][j]+1,edit[i][j-1]+1,edit[i-1][j-1]+d)
return edit[len(s1)][len(s2)]
t = test('batyu','beauty')
print(t)
根据最小编辑距离的算法思路很容易让我们想到生成指定编辑距离的单词,方法如下:

代码如下:
def generate_edit_one(s):
'''
生成所有距离为1的所有字符串列表
:param s:
:return:
'''
letters = 'qwertyuioplkjhgfdsazxcvbnm'
splits = [(s[:i],s[i:]) for i in range(len(s)+1)]
inserts = [L+c+R for L,R in splits for c in letters]
deletes = [L+R[1:] for L,R in splits if R]
replaces = [L+c+R for L,R in splits if R for c in letters]
return set(inserts+deletes+replaces)
def generate_edit_two(s):
'''
编辑距离不大于2的所有字符串
:param s:
:return:
'''
return [e2 for e1 in generate_edit_one(s) for e2 in generate_edit_one(e1)]

















)


