1 引言
2006-2020发表的有关推荐系统去偏的论文统计:
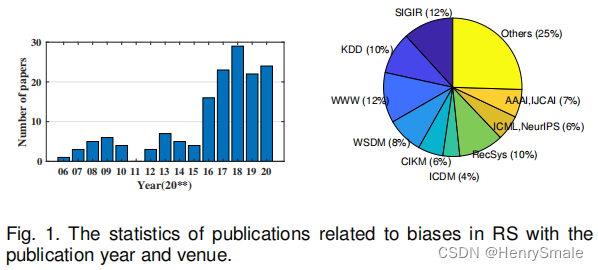
2 推荐系统的偏差
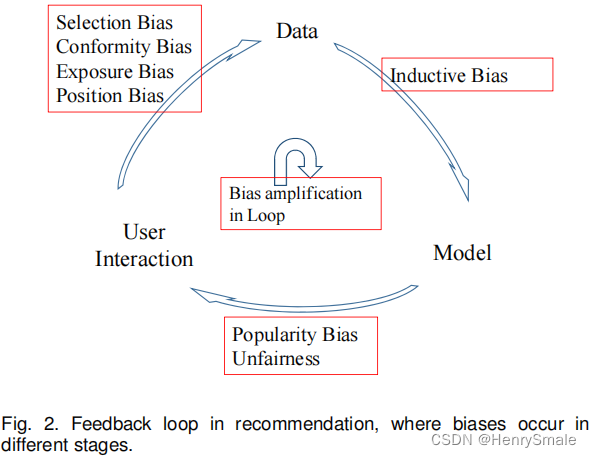
偏差发生在推荐系统的不同阶段:
- 用户交互到生成数据的阶段:
– 选择偏差:
– 一致性偏差(从众偏差):
– 曝光偏差:
– 位置偏差: - 数据到模型的阶段:
– 归纳偏差: - 模型到用户交互阶段:
– 流行度偏差:
– 不公平带来的偏差:
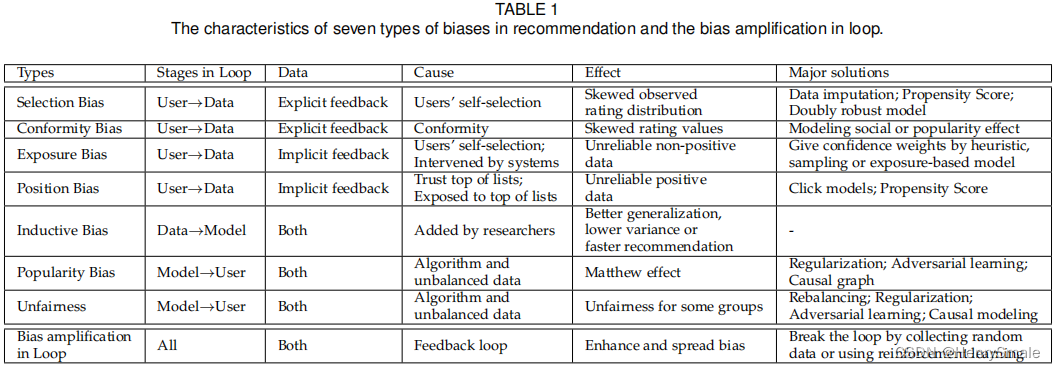
2.1 在数据上的偏差
2.1.1 在显式反馈上的偏差
(1)选择偏差
根据下图有两个发现:
- 用户倾向于选择他喜欢的商品进行评分;
- 用户尤其喜欢对他认为好的或者差的商品进行评分。
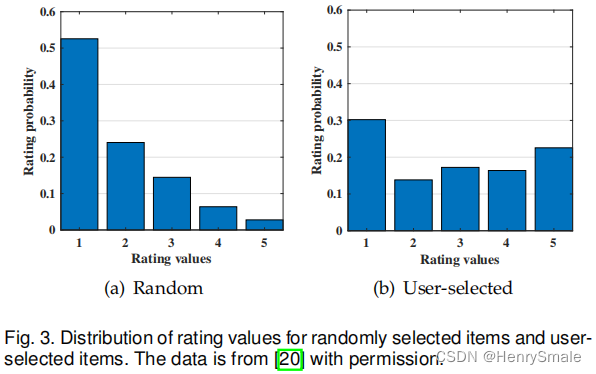
(2)一致性偏差
用户倾向于和组内的其他人评分保持一致。

2.1.2 在隐式反馈上的偏差
(1)曝光偏差
当用户只接触特定项目的一部分时,会出现暴露偏差,因此未观察到的交互并不总是代表负面偏好。


(2)位置偏差
位置偏差发生在用户倾向于与推荐列表中较高位置的项目交互时,而不管项目的实际相关性如何,因此交互的项目可能不是高度相关的。
2.2 在模型上的偏差
归纳偏差是指模型为更好地学习目标函数和对训练数据以外的数据进行泛化而做出的假设。
将预测推广到未见的例子的能力是机器学习的核心。如果没有对数据或模型的假设,就无法实现泛化,因为看不见的示例可能具有任意的输出空间。类似地,构建RS需要添加一些关于目标函数性质的假设。例如Johnson et al.[38]假设可以通过嵌入内积来估计一个交互作用,而He et al.[39]则采用神经网络作为更好的泛化方法。除了目标函数,在其他方面增加了归纳偏差。一个例子是自适应负采样器[40],[41],[42],[43],它旨在对“困难的”实例进行过采样,以提高学习速度,即使最终的损失函数将与原来的显著不同。另一个例子是离散排序模型[44],[45],[46],它将用户和商品作为二进制代码嵌入,以提高推荐效率为代价,牺牲了表示能力。
2.3 在推荐结果上的偏差和不公正
2.3.1 流行性偏差
受欢迎的项目甚至比它们的受欢迎程度更频繁地被推荐。

忽视流行偏见会导致很多问题:
-
- 它降低了个性化的水平,伤害了意外发现。由于不同用户的偏好是不同的,总是推荐流行的项目会损害用户体验,特别是对于喜欢小众项目的用户。
-
- 降低了推荐结果的公正性。受欢迎的商品并不总是高质量的。过度推荐受欢迎的商品会降低其他商品的可见性,即使它们非常匹配,这是不公平的。
-
- 大众偏见会进一步增加热门项目的曝光机会,使热门项目更加受欢迎——为未来培训收集的数据变得更加不平衡,产生所谓的“马太效应”问题。
2.3.2 不公平
推荐算法系统地、不公平地歧视某些个人或个人群体,而偏袒其他人。

2.4 反馈回路放大偏差
现实世界的推荐系统通常会产生一个有害的反馈循环。前面的小节总结了在循环的不同阶段中发生的偏差,而这些偏差可能会随着时间的推移在循环中进一步加强。以位置偏差为例,排名靠前的项目通常受益于更大的流量,这反过来提高了它们的排名突出度和接收的流量,从而导致一个更富的场景[36]。许多研究者还研究了反馈回路对受欢迎度偏差[57],[58],[59]的影响。他们的模拟结果表明,反馈循环会放大流行偏差,受欢迎的项目变得更受欢迎,不受欢迎的项目变得更不受欢迎。这些被放大的偏见还会减少多样性,加剧用户的同质化,产生所谓的“回音室”或“过滤气泡”[60],[61]。
3 推荐方法上的偏差
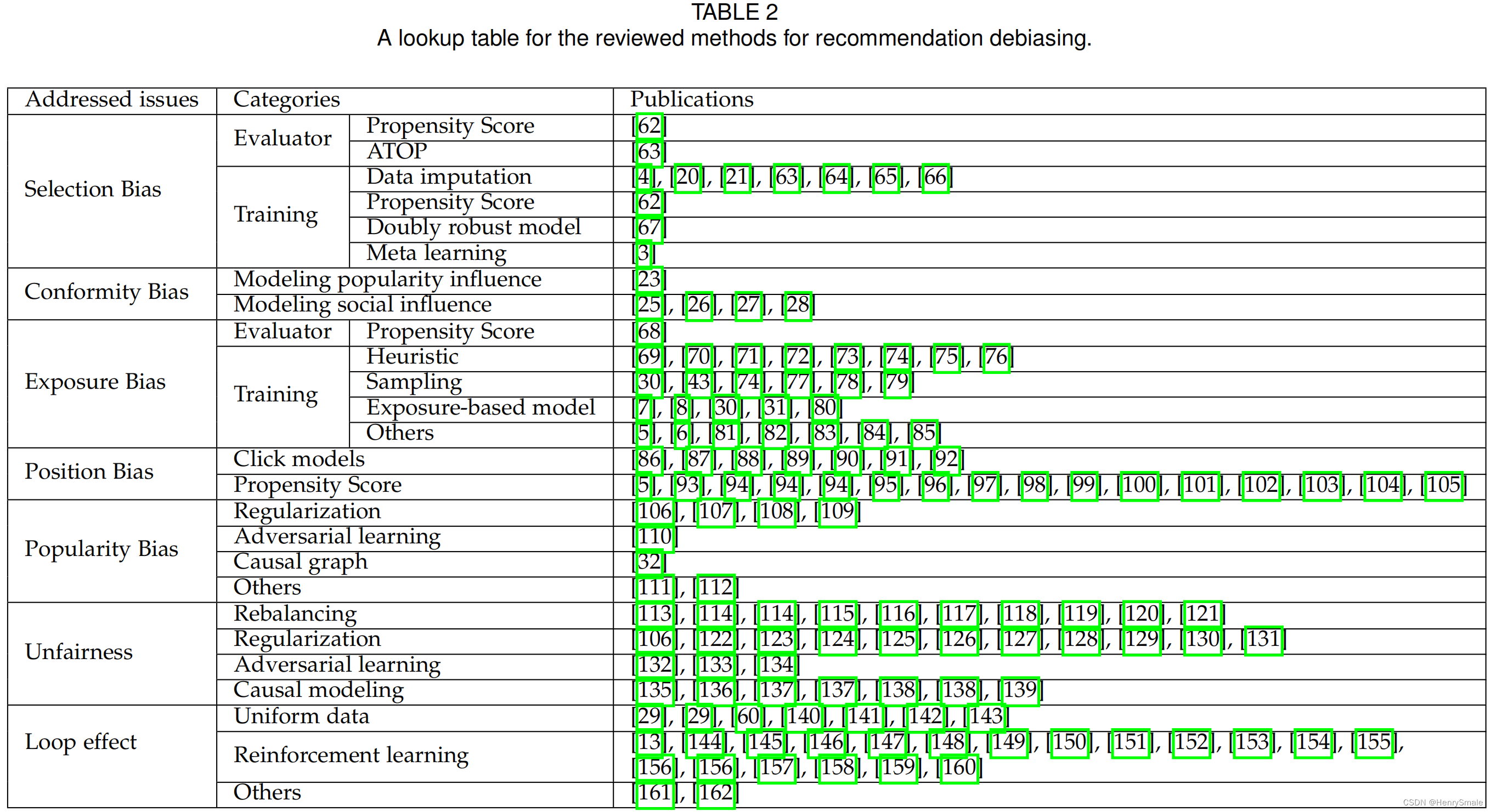
表2列出了已有的推荐算法处理的偏差类型及采用的方法:
3.1 推荐算法上的选择偏差
在观察到的评分数据上训练和测试推荐模型会产生选择偏差,因为观察到的评分并不是所有评分的代表性样本。本节首先介绍如何在有偏差的评分数据下评估推荐模型,然后回顾在推荐训练中减轻选择偏差的四种方法。
3.1.1 在评价指标上的去偏
常用的评价指标有 Mean Absolute Error (MAE), Mean Squared Error (MSE), Discounted Cumulative Gain@k (DCG@k) or Precision (Pre@k):
H(R^)=1nm∑u=1n∑i=1mδu,i(r,r^)(1)H(\hat{R})=\frac{1}{n m} \sum_{u=1}^{n} \sum_{i=1}^{m} \delta_{u, i}(r, \hat{r}) \tag1 H(R^)=nm1u=1∑ni=1∑mδu,i(r,r^)(1)
MAE:δu,i(r,r^)=∣ru,i−r^u,i∣MSE:δu,i(r,r^)=(ru,i−r^u,i)2(2)\begin{array}{c} \mathrm{MAE}: \delta_{u, i}(r, \hat{r}) & = & \left|r_{u, i}-\hat{r}_{u, i}\right| \\ \mathrm{MSE}: \delta_{u, i}(r, \hat{r}) & = & \left(r_{u, i}-\hat{r}_{u, i}\right)^{2} \end{array} \tag2 MAE:δu,i(r,r^)MSE:δu,i(r,r^)==∣ru,i−r^u,i∣(ru,i−r^u,i)2(2)
此处:
- ru,ir_{u, i}ru,i:用户uuu对商品iii的评分;
- r^u,i\hat{r}_{u, i}r^u,i:用户uuu对商品iii的预测评分。
DCG@k:δu,i(r,r^)=(I/log(rank(r^u,i)))ru,iPre@k:δu,i(r,r^)=(I/k)ru,i⋅1{rank(r^u,i)≤k}(3)\begin{array}{c} \mathrm{DCG@k}: \delta_{u, i}(r, \hat{r})&=&\left(I / \log \left(\operatorname{rank}\left(\hat{r}_{u, i}\right)\right)\right) r_{u, i}\\ \mathrm{Pre@k}: \delta_{u, i}(r, \hat{r})&=&(I / k) r_{u, i} \cdot \mathbf{1}\left\{\operatorname{rank}\left(\hat{r}_{u, i}\right) \leq k\right\} \end{array} \tag3 DCG@k:δu,i(r,r^)Pre@k:δu,i(r,r^)==(I/log(rank(r^u,i)))ru,i(I/k)ru,i⋅1{rank(r^u,i)≤k}(3)
此处: - III:?
- kkk:?
- log(rank(r^u,i))\log \left(\operatorname{rank}\left(\hat{r}_{u, i}\right)\right)log(rank(r^u,i)):?
- 1{rank(r^u,i)≤k}\mathbf{1}\left\{\operatorname{rank}\left(\hat{r}_{u, i}\right) \leq k\right\}1{rank(r^u,i)≤k}:?
由于真实评分通常是部分观察到的,传统的评价通常只使用观察到的条目的平均值:
H^naive (r^)=1∣{(u,i):Ou,i=1}∣∑(u,i):Ou,i=1δu,i(r,r^)(4)\hat{H}_{\text {naive }}(\hat{r})=\frac{1}{\left|\left\{(u, i): O_{u, i}=1\right\}\right|} \sum_{(u, i): O_{u, i}=1} \delta_{u, i}(r, \hat{r}) \tag4 H^naive (r^)=∣{(u,i):Ou,i=1}∣1(u,i):Ou,i=1∑δu,i(r,r^)(4)
这不是对真实性能的无偏估计:
EO[H^naive (r^)]≠H(r^)(5)E_{O}\left[\hat{H}_{\text {naive }}(\hat{r})\right] \neq H(\hat{r}) \tag5 EO[H^naive (r^)]=H(r^)(5)
- H^naive (r^)\hat{H}_{\text {naive }}(\hat{r})H^naive (r^)为期望除以观测概率。这种差距是由选择偏差造成的,这使得观察到的评分不是所有评分的代表性样本。
参考文献
Bias and Debias in Recommender System: A Survey and Future Directions












)




的源代码列表-1)

