1 用途

现在假如有一个需求, 把一个很长的字符串用二进制编码的形式存储, 要尽可能的占用较小空间, 那么应该怎么存储呢. 肯定是要确定每个字母的编码方法, 比如 001是A, 010是B等. 那么要怎么确定每个字符编成什么二进制码从而使得总长度最短? 一个根本思想是, 出现频率高的字母尽量编码短一些, 出现频率少的字符长一些. 这样就需要有一种方法去确定每个字符的二进制编码的方法, 需要构建一棵树 --- 哈夫曼树.

2 方法

举个例子, 现有一个字符串, 其中所有字符出现频率如下:

A: 60, B: 45, C: 13 D: 69 E: 14 F: 5 G:3

1. 把字符频率表按照频率从大到小排序

排序如下:

D: 69, A: 60, B: 45, E: 14, C: 13, F: 5, G:3

2. 把当前字符频率表的最后两个取出, 作为兄弟节点构建成二叉树, 其规则为: 频率小在左, 二者父节点为二者频率之和

取出目前频率最小的两个节点: F和G, 如图所示:

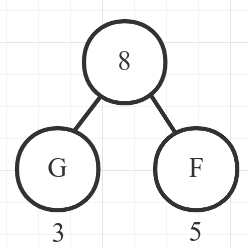
3. 把二者作为一个元素重新放入频率表(频率表还是要按照频率排序)

此时为:

D: 69, A: 60, B: 45, E: 14, C: 13, FG:8

4. 重复23步, 直至所有构建哈夫曼树完成

此时最后两个元素为C: 13和FG: 8, FG在左, C在右:

更新频率表:

D: 69, A: 60, B: 45, CFG:21, E: 14

选择E和CFG构建:

更新频率表:

D: 69, A: 60, B: 45, CFGE: 35

选择B和CFGE构建:

更新频率表:

BCFGE: 80, D: 69, A: 60

选择D和A构建:

更新频率表:

DA: 129, BCFGE: 80

选择DA, BCFGE构建, 完成:

把所有边按照左0右1进行标注:

将每个字符, 按照从根节点到其的所有边的码连接起来, 就是每个字符的编码. 对应如下:

A: 10

B: 01

C: 0011

D: 11

E: 000

F: 00101

G: 00100

这样, 利用哈夫曼树来进行字符串编码就完成了.

那么, 为什么能够保证一大长串的二进制码解析出来的是唯一的呢, 首先思考, 什么情况会导致我们解析现有编码会有多种选项呢? 假如当前正在解析二位码01, 此时已经有对应的字母了, 但是发现011或者010还可以解析成另一个字符, 这样就会有多种解码方法, 但是会发现, 哈夫曼树额每个字符都在叶节点上, 也就是说01如果对应了字符, 就不会存在010或者011也为字符的情况, 从而消除了多重解码的困惑.