1 简介
可以用阶数来描述B树, 一棵M阶B树代表着该B树最多有M个孩子节点. 如果M为2, 那么该B树就是一棵二叉搜索树. 一棵M阶B树具有以下性质:
1. 每个节点最多有M - 1个关键字. 跟普通的树不同, B树的关键字有多个.
2. 根节点最少可以只有一个关键字.
3. 非根节点至少有k个关键字, 这里的k是指ceil(M / 2) - 1.(这里面的ceil是指大于等于参数的最小整数, 从下面插入操作分析可知, 叶子节点都是由父节点分裂而来, 而分裂的条件就是分裂前节点总数已经达到了M)
4. 每个节点中的关键字都按照从小到大的顺序排列, 每个关键字在左子树中的所有关键字都小于它本身的关键字, 右子树的都大于它本身关键字.
5. 所有叶子节点都位于同一层, 或者说根节点到每个叶子节点的长度都相同.
2 插入操作
一棵M阶树的插入操作可以总结为以下步骤:
1. 根据要插入的key的值, 找到对应的叶子节点(一定要注意是叶子节点)
2. 如果被插入后的节点的key总数达到了M, 就需要对该节点, 按照key序列的中间左右分开进行分裂, 中间的key插入其父节点.
3. 对父节点进行第二步检查.
下面以一棵5阶B树的插入操作举例:
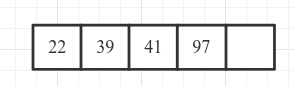
1. 首先插入39, 22, 97, 41:
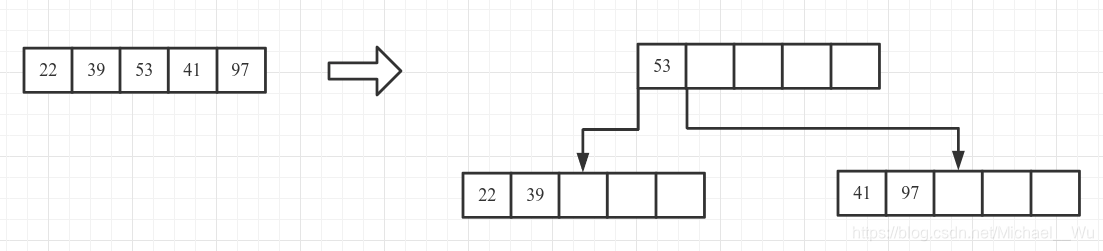
2. 插入39, 节点总key数量达到了5, 进行分裂:
3. 插入13, 21:
4. 插入40, 节点分裂, 22进入父节点:
5. 插入30, 27, 33, 其中33插入后, 该节点满, 导致其分裂, 33进入父节点:
6. 插入36, 35, 34, 其中34插入后, 该节点满, 导致节点分裂, 36进入父节点:
7. 插入24, 29:
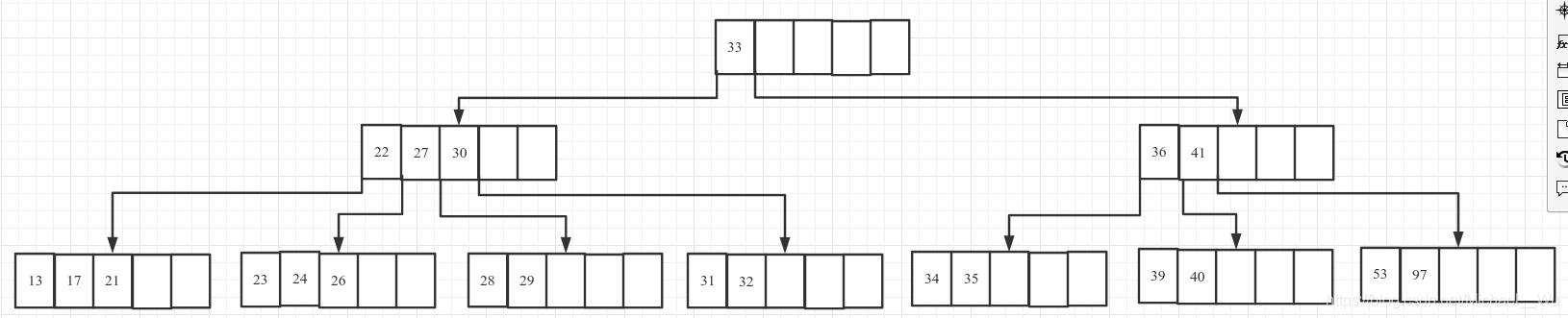
8. 插入26, 导致该节点满, 分裂, 27 进入父节点, 然后父节点也满了, 再分裂, 创建新节点:
3 删除操作
1. 首先找到要删除的点, 如果点不在树中, 那么肯定删除失败了.
2. 如果要删除的节点位于叶子节点, 那么拿掉这个节点, 如果位于非叶子节点上, 那么就要找到其后继节点, 因为后继节点肯定位于叶子节点上(因为肯定位于最左, 如果还位于非叶上面, 因其左子节点肯定存在比其大的节点, 不可能出现这种情况), 把要删除的节点替换成后继节点的值, 然后删除后继节点.
3. 因为最终删除的点位于叶子上, 所以要观察此时该叶节点是否满足B树的性质3:
非根节点至少有k个关键字, 这里的k是指ceil(M / 2) - 1
如果满足, 那么结束删除操作, 如果不满足, 那么进行4.
4. 先观察兄弟节点的情况:
如果兄弟节点的key数量大于k, 那么把父亲节点的key下移至该节点, 并把兄弟节点的一个节点上移至父节点
否则, 将父节点中的key下移与当前节点及其兄弟节点中的key合并, 形成一个新的节点. 原父节点中的key的两个孩子指针就变成了一个孩子指针, 指向这个新节点, 然后当前节点的指针指向父节点, 重复第3步.
举例说明:
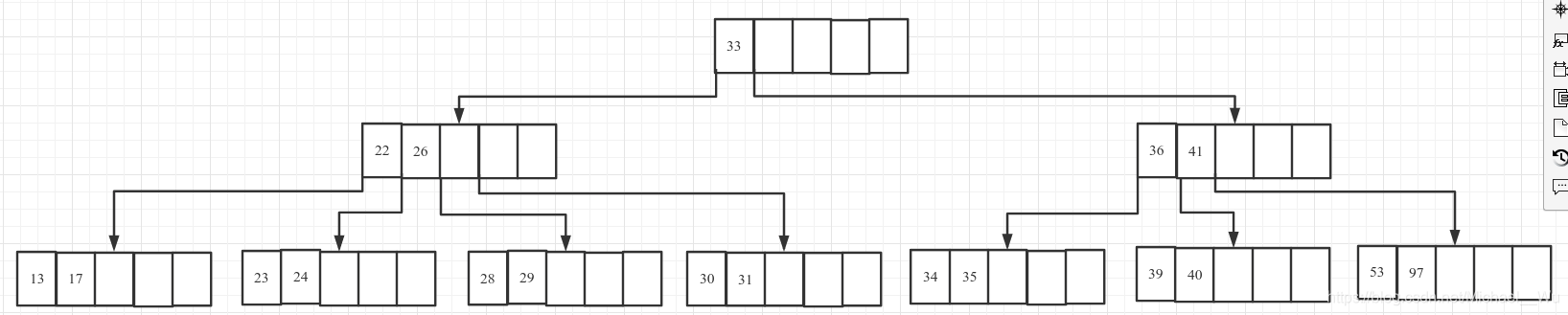
1. 原始状态5阶B树, 每个非根节点的最少关键字数量为ceil(5 / 2) - 1 = 2:
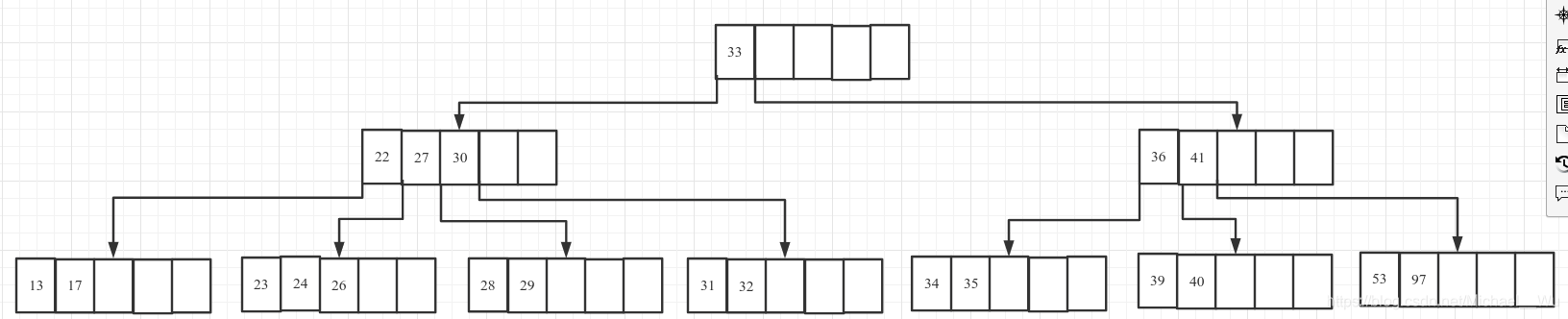
2. 删除21, 位于叶节点, 且删除完成后该节点关键字数量为2, 结束:
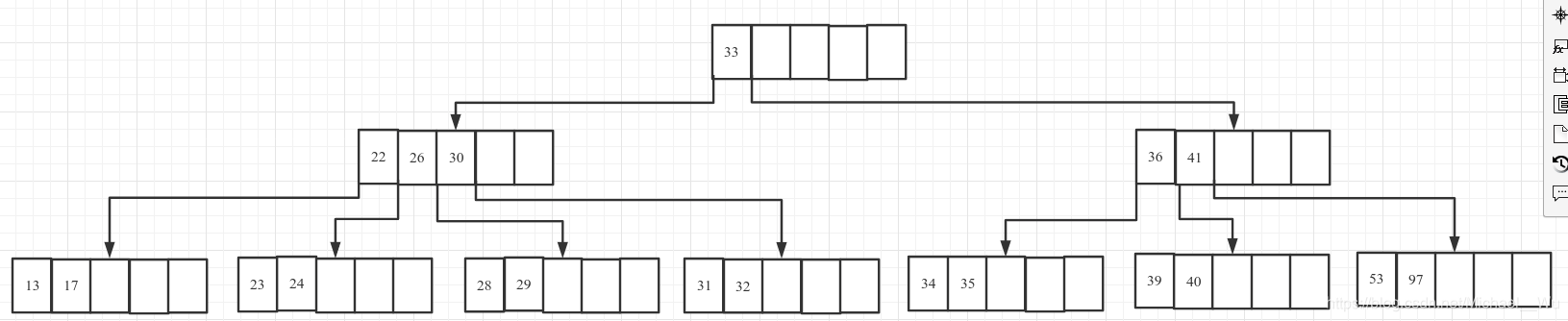
3. 删除27, 27位于非叶子节点上
3.1 首先把其值修改为后继节点28:
3.2 删除28, 28位于叶子节点上, 删去:
3.3 此时该节点key数量小于2, 其左边的兄弟节点有三个key, 可以把父节点一个key移下来, 把兄弟节点一个key移到父节点, 具体操作就是把28下移, 26上移, 完成:
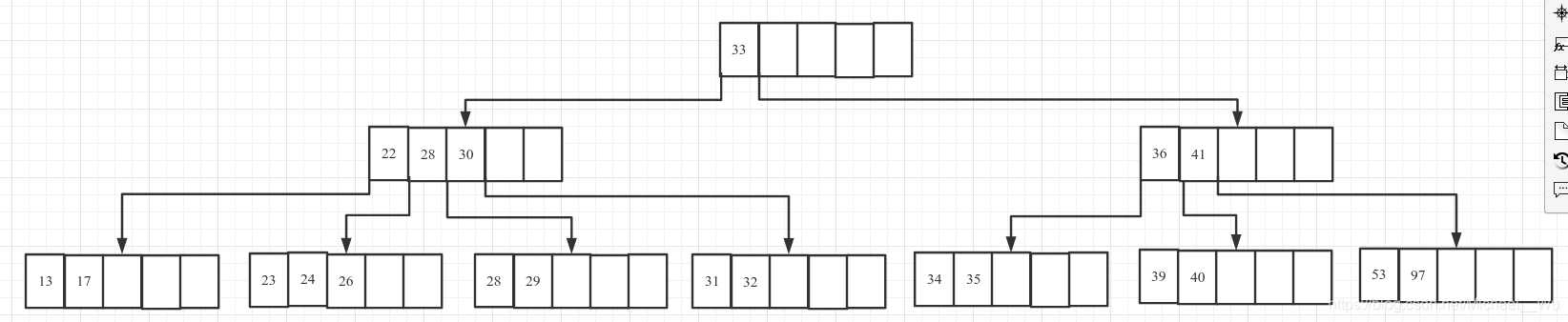
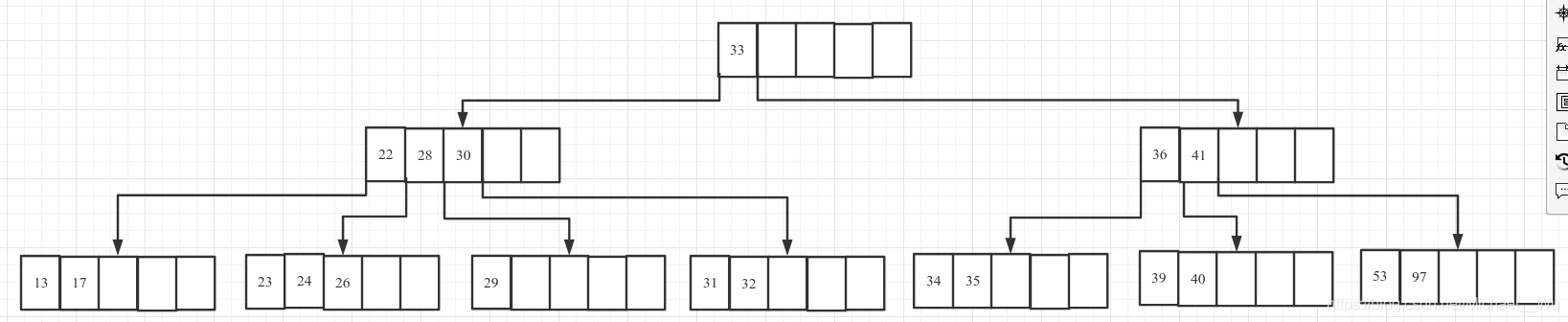
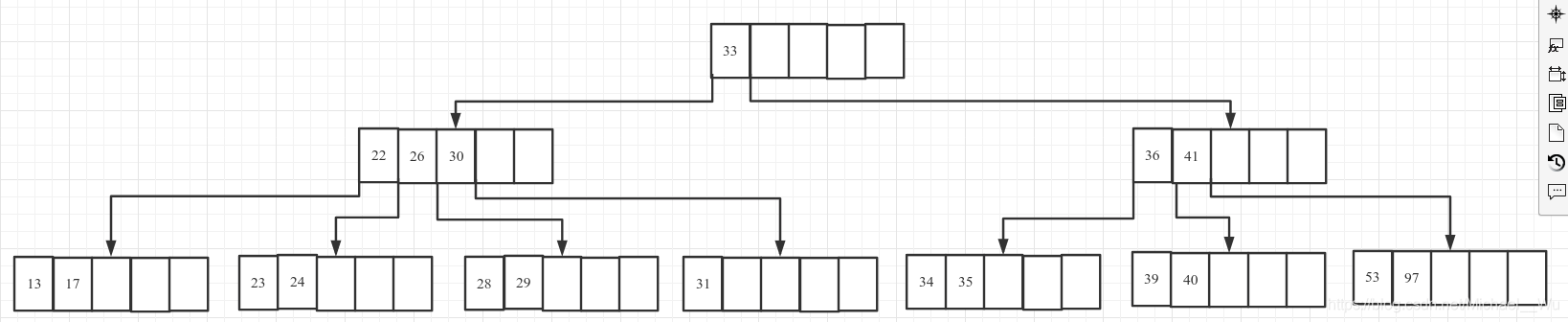
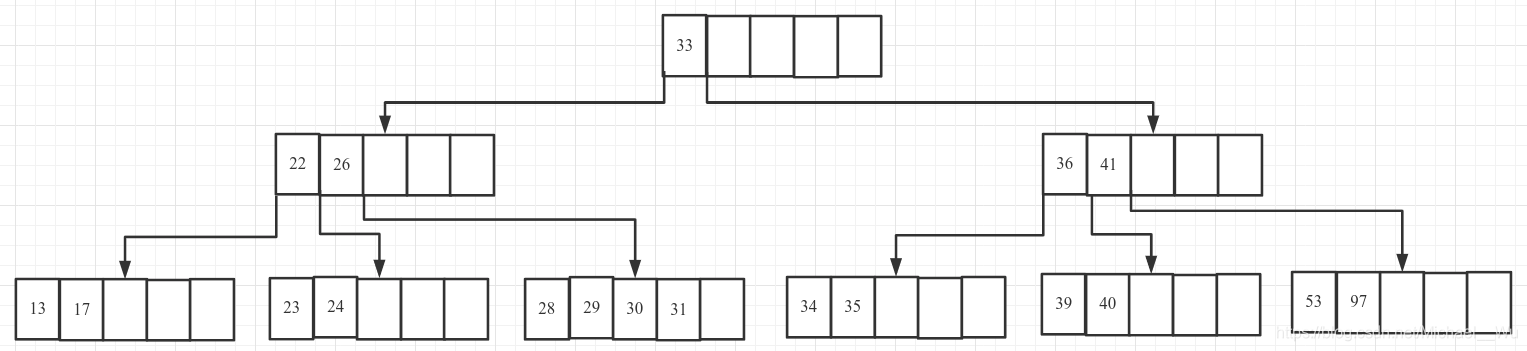
4. 删除32
4.1 首先删除32:
4.2 该节点key数量为1, 小于2, 而兄弟节点也没有大于2的了, 所以让父节点中对应的key30下移与该节点和兄弟节点合并:
