1.超前进位加法器
看了一些面经,提到会让你用基础的门搭加法器,因此首先得熟悉半加器,全加器等最基础的加法器才能理解之后的超前进位加法器,树型加法器等复杂的加法器。
半加器的输入为a,b,输出为结果s和进位c,则其关系为
全加器的输入多了一个进位cin,输出为结果位s和进位输出cout,则其关系为
使用多个全加器级联,把每一级的进位输出作为下一级的进位输入即构成了行波进位加法器,其加法过程是很好理解的,就是从最低位开始一位一位运算,并且把低位的进位加到高位上,与手算的思路是一致的。其结构如图所示。

但若是画出其门级的电路图我们会发现,由于采用级联结构,行波进位加法器的关键路径非常长,N比特行波进位加法器的最长路径位
则对于N比特超前进位加法器,其结果位和进位可写成如下的形式
则通过迭代
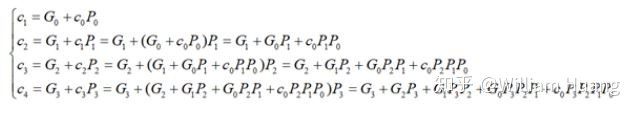
则对应的,超前进位加法器结构如图所示。
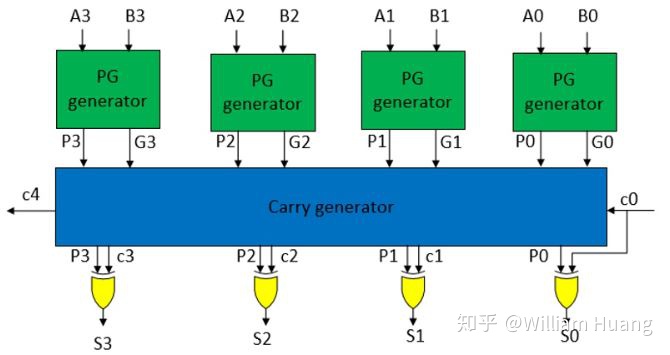
对于更大位宽的,例如32,64bit的加法运算,为了避免造成电路的扇入扇出过大,会用多个4bit超前进位加法器级联,从而获得一个折中的解决方案。
从关键路径上来看,4bit超前进位加法器的进位都只需要经过3级门电路延迟即可得到,相比较于行波进位加法器有巨大的优势,即使级联构成更大位宽的加法器仍然缩短了关键路径的长度。
2.Wallace树型结构
话说这Wallace是不是该翻译成华莱士呢,嗯~亦可赛艇啊。
要理解Wallace树需要先理解进位保存加法器。进位保存加法器以三个树作为输入,输出两个数,这两个数相加即为最终的加法结果,因此进位保存加法器相当于进行了一次压缩过程,将三个数的加法压缩为两个数的加法。然而进位保存加法器并不是什么新奇的黑科技,而是全加器的一个变形,如下图所示。
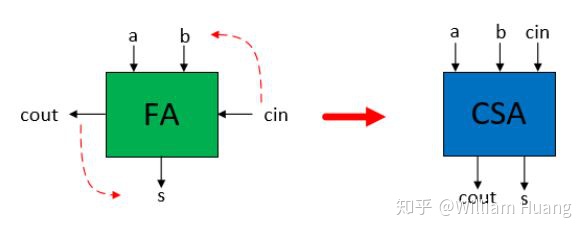
从图中可以看出,进位保存加法器就是对全加器进行重新包装。
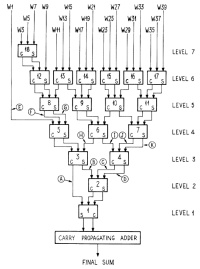
熟悉了进位保存加法器后我们就可以来看Wallace树型结构了,其总体结构如下图所示。
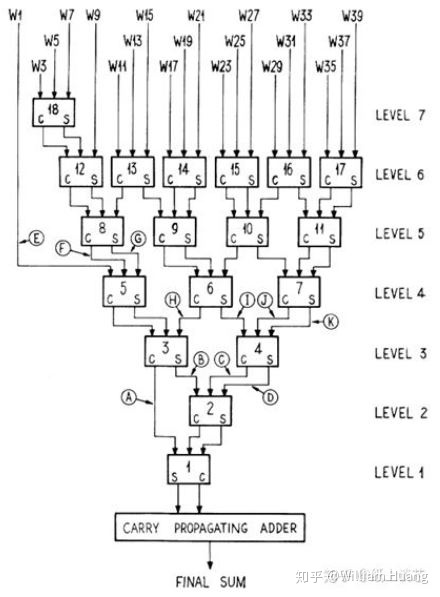
可以看出,树型结构就是将多个加数分组,每三个分为一组后,经过进位保存加法器压缩为2个数,如此迭代循环得到最终加法的结果。
在乘法器中,乘法的积是多个部分和之和,若使用普通加法器,则需等待前面的部分和计算完成才能计算后面的部分和,延迟较高,因此可以使用Wallace树型结构,对部分和进行分组计算得到最后的总和结果,即为乘法的积。
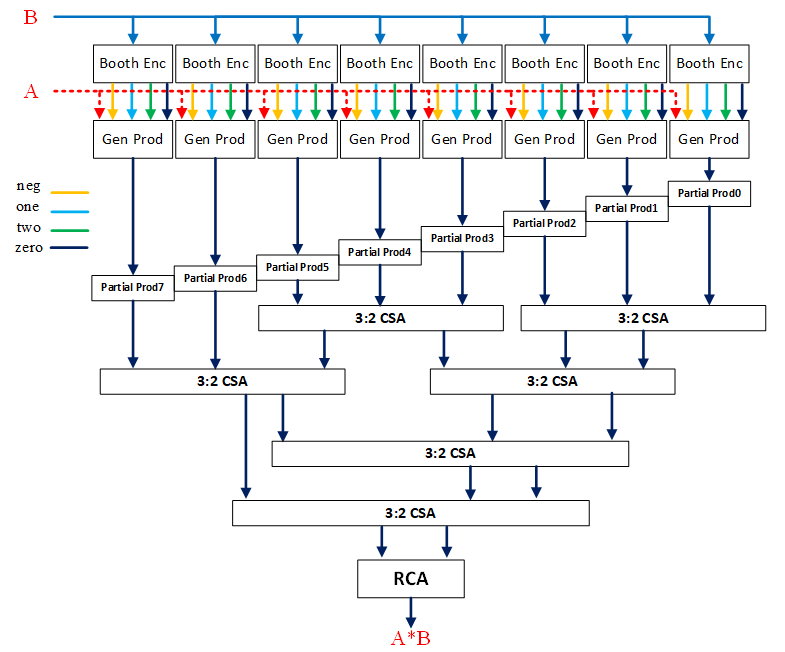
3.Booth乘法器
若是用补码表示一个数,则其转换为十进制的计算方式为
将其展开,并令
此时再计算乘法
从上式可以看出,这样变化的优势是若B的某相邻两位相同,则可以省去运算而只进行移位即可。如果
以上是Radix-2 Booth算法的推导,其算法流程如下
1.被乘数和乘数分别放入A,B寄存器,中间结果放入M,B寄存器。
2.另设置一个1bit的寄存器。将M,
寄存器初始为0。
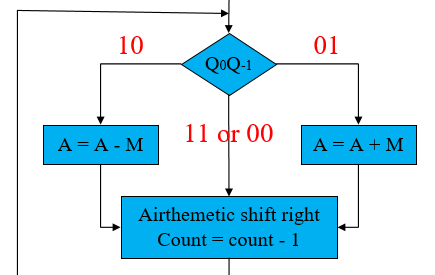
3.在每个周期检查寄存器。
4-1.若= 00 或 11,将{
}直接右移1bit。
4-2.若{} = 01,则A与M相加,将{
}直接右移1bit。
4-3.若{} = 10,则A与M相减,将{
}直接右移1bit。
5.最终的结果即为{M,B},是乘法积的补码表示。
需要注意的是,上述所有数都是补码表示,且上述右移操作需保留符号位,即保持M的最高位不变。
在实际应用中较常用的是Radix-4 Booth乘法器,与Radix-2类似,其算法可通过原始的补码计算式展开得到
上式中的
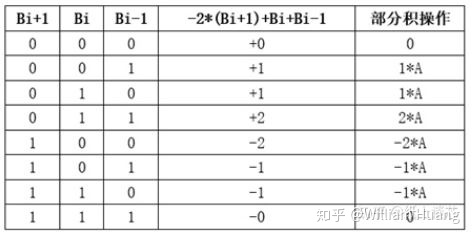
不难看出,相较于Radix-2 Booth算法,Radix-4 Booth算法需要的循环次数更少,因此在实际中应用更加广泛。
参考链接
关于乘法器和加法器,如下的专栏讲述的非常详细,可以作为参考。
纸上谈芯:【HDL系列】超前进位加法器原理与设计zhuanlan.zhihu.com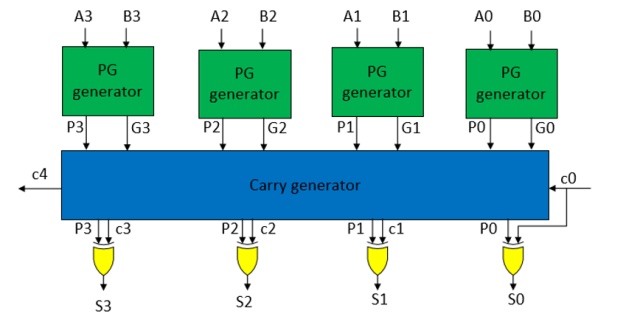
)







)




)
当被NTR剧情虐到的时候怎么办)




