目录
朴素贝叶斯==基于样本特征来预测样本属于的类别y
朴素贝叶斯算法的基本概念与核心思想
假设两个特征维度之间是相互独立的
拉普拉斯平滑=增加出现次数=保证0不出现
编辑 基于样本特征来预测样本属于的类别y
什么是拉普拉斯平滑
朴素贝叶斯==基于样本特征来预测样本属于的类别y
朴素贝叶斯算法的基本概念与核心思想
首先我们来讨论一下朴素贝叶斯算法里面涉及到的几个核心概念:先验概率、后验概率、联合概率、全概率公式、贝叶斯公式。
想象这样一个场景,在一个炎热夏天的午后,我们想整个又大又甜的西瓜来清爽一下。于是我们一路小跑的来到超市,到超市以后我们需要选一个又大又甜的西瓜。我们根据常识或是经验知道放在超市里面卖的西瓜,一般情况下是熟的,假设根据统计,在超市里面卖的西瓜成熟的概率是70%,这个概率就是先验概率,先验概率(prior probability)就是根据以往经验和分析得到的概率。
因为是西瓜成熟的概率是 70%,所以还有 30% 的西瓜没有熟,所以我们还是需要好好挑一挑。那我们根据什么选择呢?作为一个吃货,我有些经验,比如瓜蒂脱落的话,西瓜成熟的概率会更高,大概是 85%。如果把瓜蒂脱落当作一种已有的结果,然后去推测西瓜成熟的概率,
这个概率 P(瓜熟 | 瓜蒂脱落) 就被称为后验概率。后验概率类似于条件概率。


假设两个特征维度之间是相互独立的
辛苦/情书=0导致误差
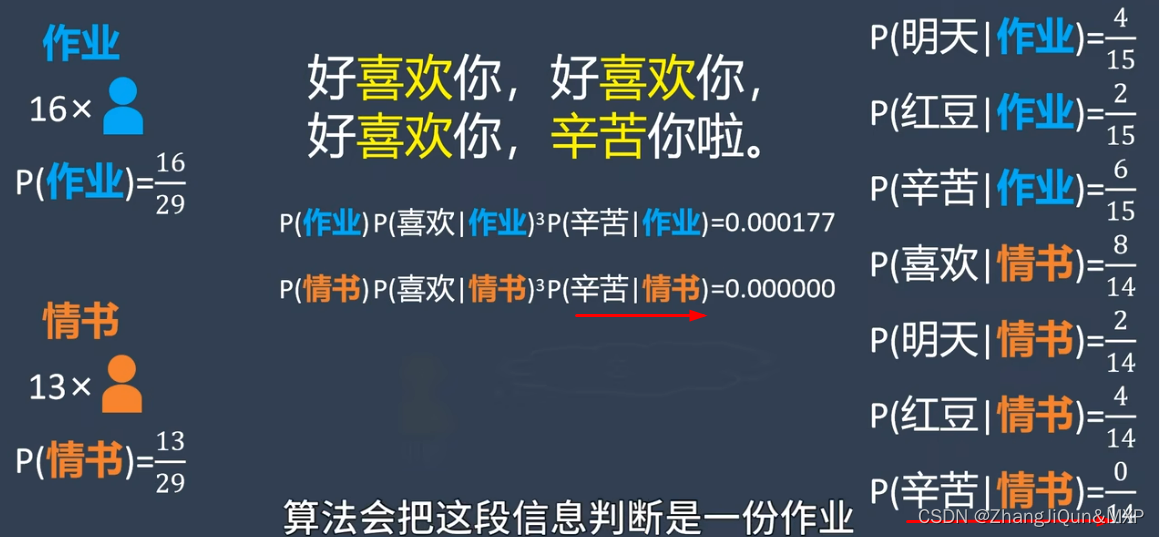
拉普拉斯平滑=增加出现次数=保证0不出现


 基于样本特征来预测样本属于的类别y
基于样本特征来预测样本属于的类别y


什么是拉普拉斯平滑
拉普拉斯平滑是朴素贝叶斯分类器中一种常用的平滑方法,它通过为每个特征的计算增加一个正数值来避免出现概率为0的情况,从而提高了分类器的准确性和可靠性。
一般情况下,在朴素贝叶斯分类器中,计算某个特征的条件概率值时,都会遇到特征值在训练集中未出现的情况,此时,如果直接根据频数统计,则估计值将为0,这一现象我们称之为“零概率问题”。拉普拉斯平滑的本质就在于对这种情况的处理。
项目范围管理 ★重点集萃★)





:虚拟机统计信息监视工具)










和逆快速傅里叶变换】生成雷达接收到的经过多普勒频移的脉冲雷达信号(Matlab代码实现))

