知识点总结

— 期末来临，你准备好了吗 —

高

等

数学

学

下

一转眼

又一学期即将结束

期末考试也悄悄地临近了

大家都准备好了吗

我们为大家带来了高等数学(下)的复习资料

来吧，展示！

1

向量代数与

空间解析几何

首先

我们看到的是向量代数与空间解析几何的重点知识

知识点导图

重点公式

该章节重点在求直线和平面的方程上

2

函数微分

学习了代数几何

让我们来看看函数微分是怎样为我们设置障碍的呐？

知识点导图

重点公式

重点公式

计算多元函数极值的方法一共有两种

第一种是普通极值

第二种条件极值(必须有条件才可以用拉格朗日乘数法)

该处的重点是偏导数，全微分已经多元复合函数求导，隐函数求导的计算，之后就是方向导数和梯度的计算以及梯度和多元函数极值之间的关系，求空间曲面的切线，法平面方程和曲面的切平面，法线方程。

3

积分

重积分部分,二重积分是必须掌握的，但是在三重积分那里难度较大，只能根据自己的掌握情况做适当的练习。在这里对三重积分不做重点的解释

 曲线积分和曲面积分，这两个积分又分别有两类，下面我们来看一下常见的解题方法

这两种曲线积分并不是毫无交集的，他们存在着一些关系，同时这里还有一个非常非常非常重要的公式，在一些题目中使用可以起到事半功倍的效果。

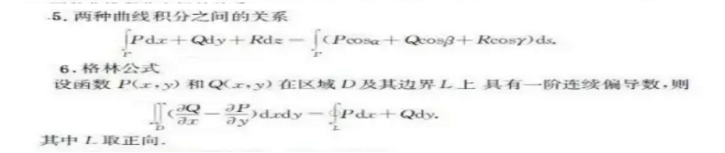
说完了曲线积分再来看看曲面积分吧！

对面积的曲面积分为第一类曲面积分，对坐标的曲面积分为第二类曲面积分，二者之间的关系如下:

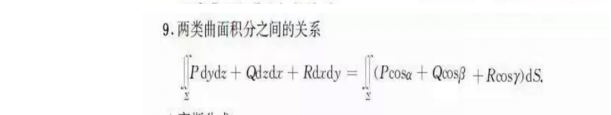
4

无穷级数

最后，我们来看一个新的知识——无穷级数

1. 在判断敛散性时，常数项级数常用比值审敛法，交错级数常用莱布尼兹定理进行判断

2. 幂级数

3. 傅里叶级数(重点掌握两个公式，一个定理)

两个公式：

一个定理：(狄利克雷充分条件)

这一章节的重点在判断级数是否收敛，求幂级数的收敛半径收敛域，求和函数，傅里叶级数

至此

高数(下)的知识就回顾完了

考试在即

大家可以找练习册上典型的题目重复练习

最后希望大家可以取得一个好的成绩

期末考试冲呀！！

END

编辑 | 王煜缇，周丰慧

审核 | 于恒海