AI应用开发基础傻瓜书系列2-神经网络中反向传播与梯度下降的基本概念

Content
01.0-神经网络的基本工作原理
01.1-基本数学导数公式
01.2-Python-Numpy库的点滴
02.0-反向传播与梯度下降
02.1-线性反向传播
02.2-非线性反向传播
02.3-梯度下降
03.0-损失函数
03.1-均方差损失函数
03.2-交叉熵损失函数
04.0-单入单出单层-单变量线性回归
04.1-最小二乘法
04.2-梯度下降法
04.3-神经网络法
04.4-梯度下降的三种形式
04.5-实现逻辑非门
05.0-多入单出单层-多变量线性回归
05.1-正规方程法
05.2-神经网络法
05.3-样本特征数据的归一化
05.4-归一化的后遗症
05.5-正确的推理方法
05.6-归一化标签值
06.0-多入多出单层神经网络-多变量线性分类
06.1-二分类原理
06.2-线性二分类实现
06.3-线性二分类结果可视化
06.4-多分类原理
06.5-线性多分类实现
06.6-线性多分类结果可视化
07.0-激活函数
07.1-挤压型激活函数
07.2-半线性激活函数
07.3-用双曲正切函数分类
07.4-实现逻辑与门和或门
08.0-单入单出双层-万能近似定理
08.1-双层拟合网络的原理
08.2-双层拟合网络的实现
09.0-多入多出双层-双变量非线性分类
09.1-实现逻辑异或门
09.2-理解二分类的工作原理
09.3-非线性多分类
09.4-理解多分类的工作原理
10.0-调参与优化
10.1-权重矩阵初始化
10.2-参数调优
10.3-搜索最优学习率
10.4-梯度下降优化算法
10.5-自适应学习率算法
11.0-深度学习基础
11.1-三层神经网络的实现
11.2-验证与测试
11.3-梯度检查
11.4-手工测试训练效果
11.5-搭建深度神经网络框架
12.0-卷积神经网络
12.1-卷积
12.2-池化
14.1-神经网络模型概述
14.2-Windows模型的部署
14.3-Android模型的部署

第二篇：神经网络中反向传播与梯度下降的基本概念

预警：本篇博客中会涉及到偏导数的概念，但是非常初级，很容易理解，建议硬着头皮看，跟着算一遍，看完之后保证会觉得人生美好了很多。

反向传播和梯度下降这两个词，第一眼看上去似懂非懂，不明觉厉。这两个概念是整个神经网络中的重要组成部分，是和误差函数/损失函数的概念分不开的。

神经网络训练的最基本的思想就是：先“蒙”一个结果，我们叫预测结果a，看看这个预测结果和事先标记好的训练集中的真实结果y之间的差距，然后调整策略，再试一次，这一次就不是“蒙”了，而是有依据地向正确的方向靠近。如此反复多次，一直到预测结果和真实结果之间相差无几，亦即|a-y|->0，就结束训练。

在神经网络训练中，我们把“蒙”叫做初始化，可以随机，也可以根据以前的经验给定初始值。即使是“蒙”，也是有技术含量的。

通俗地理解反向传播

举个通俗的例子，Bob拿了一支没有准星的步枪，或者是准星有bug，或者是Bob眼神儿不好看不清靶子，或者是雾很大…反正就是Bob很倒霉。第一次试枪后，拉回靶子一看，弹着点偏左了，于是在第二次试枪时，Bob就会有意识地向右侧偏几毫米，再看靶子上的弹着点，如此反复几次，Bob就会掌握这支步枪的脾气了。下图显示了Bob的5次试枪过程：

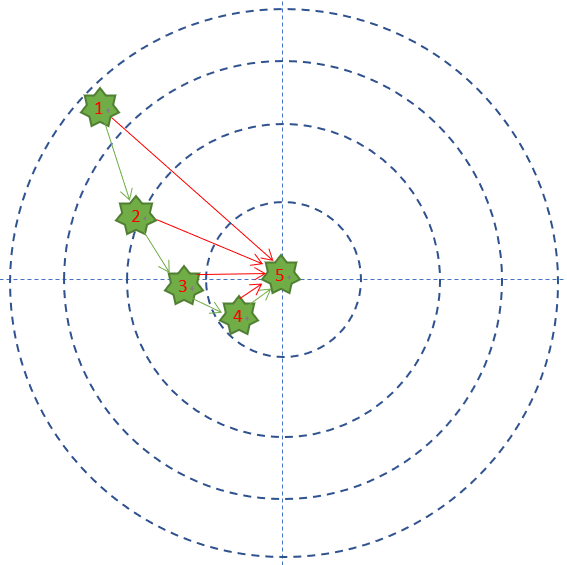
在这个例子中：

每次试枪弹着点和靶心之间的差距就叫做误差，可以用一个误差函数来表示，比如差距的绝对值，如图中的红色线。
一共试枪5次，就是迭代/训练了5次的过程。
每次试枪后，把靶子拉回来看弹着点，然后调整下一次的射击角度的过程，叫做反向传播。注意，把靶子拉回来看和跑到靶子前面去看有本质的区别，后者容易有生命危险，因为还有别的射击者。一个不恰当的比喻是，在数学概念中，人跑到靶子前面去看，叫做正向微分；把靶子拉回来看，叫做反向微分。
每次调整角度的数值和方向，叫做梯度。比如向右侧调整1毫米，或者向左下方调整2毫米。如图中的绿色矢量线。

上图是每次单发点射，所以每次训练样本的个数是1。在实际的神经网络训练中，通常需要多个样本，做批量训练，以避免单个样本本身采样时带来的误差。在本例中，多个样本可以描述为连发射击，假设一次可以连打3发子弹，每次的离散程度都类似，如下图所示：

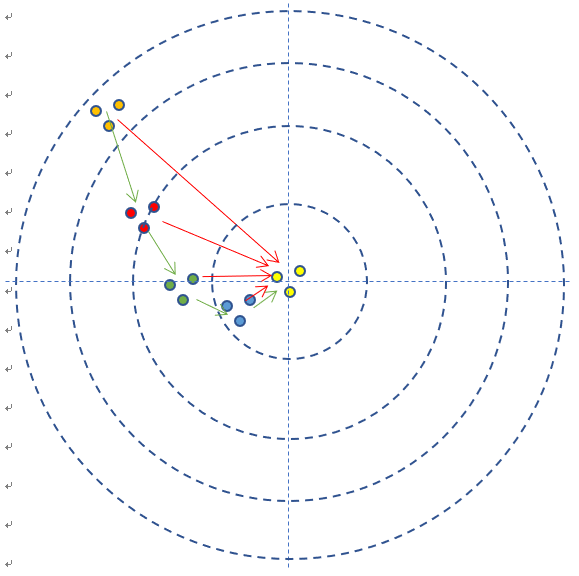
如果每次3发子弹连发，这3发子弹的弹着点和靶心之间的差距之和再除以3，叫做损失，可以用损失函数来表示。

其实损失就是所有样本的误差的总和，所以有时候损失函数可以和误差函数混用概念。

其实射击还不这么简单，如果是远距离狙击，还要考虑空气阻力和风速，在神经网络里，空气阻力和风速可以对应到隐藏层的概念上。

用数学概念理解反向传播

我们再用一个纯数学的例子来说明反向传播的概念。

假设我们有一个函数
$z = x * y ，其中 : x = w * 2 + b, y = b + 1 ，即 : z = (w * 2 + b) * (b + 1)$

关系如下图：

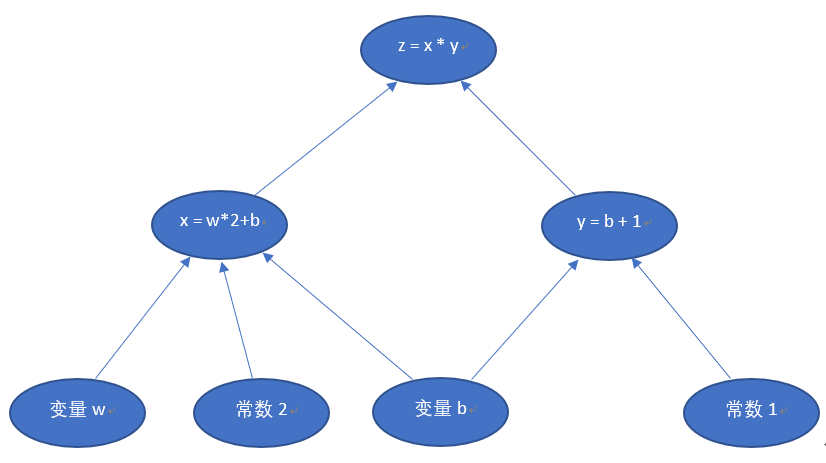
注意这里x,
y, z不是变量，w,
b是才变量，因为在神经网络中，我们要最终求解的是w和b的值，x,y,z只是样本值。

当w = 3,
b = 4时，会得到如下结果

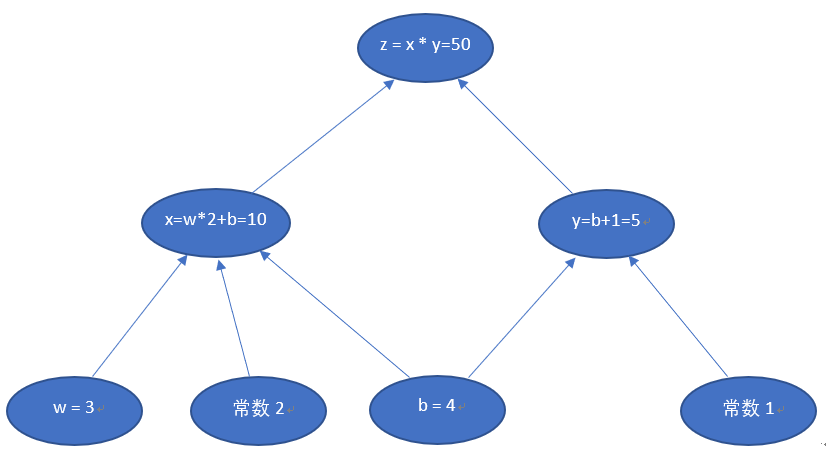
最终的z值，受到了前面很多因素的影响：变量w，变量b，计算式x，计算式y。常数是个定值，不考虑。目前的z=50，如果我们想让z变大一些，w和b应该如何变化呢？

我们从z开始一层一层向回看，图中各节点关于变量b的偏导计算结果如下图：

因为z = x

y，其中x = w
2 + b，y = b +
1

所以：

$∂z∂b=∂z∂x∗∂x∂b+∂z∂y∗∂y∂b=5∗1+10∗1=15\frac{\partial{z}}{\partial{b}}=\frac{\partial{z}}{\partial{x}}*\frac{\partial{x}}{\partial{b}}+\frac{\partial{z}}{\partial{y}}*\frac{\partial{y}}{\partial{b}}=5*1+10*1=15$

其中：

$∂z∂x=∂∂x(x∗y)=y=5\frac{\partial{z}}{\partial{x}}=\frac{\partial{}}{\partial{x}}(x*y)=y=5$

$∂z∂y=∂∂y(x∗y)=x=10\frac{\partial{z}}{\partial{y}}=\frac{\partial{}}{\partial{y}}(x*y)=x=10$

$∂x∂b=∂∂b(w∗2+b)=1\frac{\partial{x}}{\partial{b}}=\frac{\partial{}}{\partial{b}}(w*2+b)=1$

$∂y∂b=∂∂b(b+1)=1\frac{\partial{y}}{\partial{b}}=\frac{\partial{}}{\partial{b}}(b+1)=1$

有一个很有趣的问题是：z
= x * y = 10 * 5 = 50，表面看起来x=10，y=5，似乎x对z的贡献较大。那么x的微小变化和y的微小变化对z来说，哪一个贡献大呢？

我们假设只有x变化时，△x =
0.1, 则z = (x

△x) * y
= 10.1 * 5 = 50.5

我们再假设只有y变化时，△y =
0.1, 则z = x *
(y +△y) = 10

5.1 = 51

50.5 < 51，说明y的微小变化对z的贡献比较大，这个从

$∂z∂x=∂∂x(x∗y)=5<∂z∂y=∂∂y(x∗y)=10\frac{\partial{z}}{\partial{x}}=\frac{\partial{}}{\partial{x}}(x*y)=5 < \frac{\partial{z}}{\partial{y}}=\frac{\partial{}}{\partial{y}}(x*y)=10$

和这两个值的比较来看也可以证明。而△x和△y就可以理解为梯度值。

同理，我们也可以得到图中各变量对w的偏导值：

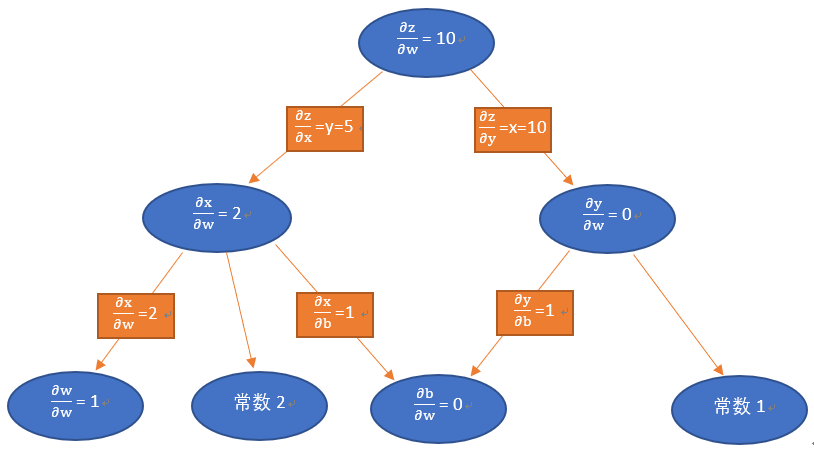
从以上两图可以看出，反向微分保留了所有变量（包括中间变量）对结果z的影响。若z为误差函数，则对图进行一次计算，可以得到所有节点对z的影响，即梯度值，下一步就可以利用这些梯度值来更新w和b的权重。

w的变化和b的变化，哪一个对z的变化贡献大？从图中还可以注意到：

$∂z∂b=15\frac{\partial{z}}{\partial{b}}=15$

$∂z∂w=10\frac{\partial{z}}{\partial{w}}=10$

所以每次w和b的变化值是不相同的，b的变化会比w大一些，也就是每一步的跨度大一些，这个是与z
= xy = (w2+b)*(b+1)这个算式相关的，并不代表神经网络中实际情况。

反向传播的实际计算过程（单变量）

还是用上面的例子，目前：

$w = 3$
$b = 4$
$x = w * 2 + b = 10$
$y = b + 1 = 5$
$z = x * y = 50$

假设我们最终的目的想让z
= 60，只改变b的值，如何实现？

答案就是偏导数：

$∂z∂b=ΔzΔb=15\frac{\partial{z}}{\partial{b}}=\frac{\Delta{z}}{\Delta{b}}=15$

目前z=50, 距离60相差10，所以我们令 $Δz=60−50=10\Delta{z}=60-50=10$ ，则：

$ΔzΔb=15=10Δb\frac{\Delta{z}}{\Delta{b}}=15=\frac{10}{\Delta{b}} \\$

所以:

$Δb=0.66667\Delta{b} = 0.66667$

再带入式子中（顺便说一句，下面这个计算过程就叫做前向计算）

$w = 3$
$b = 4 + 0.66667 = 4.66667$
$x = w * 2 + b = 10.66667$
$y = b + 1 = 5.66667$
$z = x * y = 10.66667 * 5.66667 = 60.4445$

一下子超过60了，咋办？再来一次（下面的过程就叫做反向传播）：

我们令 $Δz=60−60.4445=−0.4445\Delta{z}=60-60.4445=-0.4445$ ，则：

$ΔzΔb=15=−0.4445Δb\frac{\Delta{z}}{\Delta{b}}=15=\frac{-0.4445}{\Delta{b}} \\$

所以:

$Δb=−0.02963\Delta{b} = -0.02963$

再带入式子中：

$w = 3$
$b = 4.66667 - 0.02963 = 4.63704$
$x = w * 2 + b = 10.63704$
$y = b + 1 = 5.63704$
$z = x * y = 10.63704 * 5.63704 = 59.96$

咦哈！59.96了！再迭代几次，应该可以近似等于60了，直到误差不大于0.00001时，我们就可以结束迭代了，对于计算机来说，这些运算的执行速度很快。

有的同学会说了：这个问题不是用数学公式倒推求解一个二次方程，就能直接得到准确的b值吗？是的！但是我们是要说明机器学习的方法，机器并不会解二次方程，而且很多时候不是用二次方程就能解决实际问题的。而上例所示，是用机器所擅长的迭代计算的方法来不断逼近真实解，这就是机器学习的真谛！而且这种方法是普遍适用的。

用二维平面函数说明梯度下降原理

很多资料中会用下面这个图来说明梯度下降，但是都没有说清楚以下几个问题：

1）为啥用这个看上去像 $y = x^2$ 族的函数来说明梯度下降？

2）在最低点的左侧，梯度值是负数；在最低点的右侧，梯度值是正数。为什么说是“下降”？

3）为什么1—>2，2—>3等等的连线不是这条曲线的切线呢，而好像是弦线？

为何用$y =

x^2$函数？

这是因为有一种损失函数的形式就是均方差，亦即：

$\sum_{i}(a_i - y_i) ^ 2$

其中a是本次迭代的预测结果，y是样本中的真实结果。我们的目的就是在这个函数上求最小值，使loss最小，这样样本值和预测值就会非常非常接近，以便于我们以后预测不在样本中的真实数据。

为什么说是“梯度下降”？

“梯度下降”，刚接触这个词时，我总是往“降低难度”或“降低维度”方面去理解，因为有个“下降”的动词在里面。而实际上，“下降”在这里面的含义是“与导数相反的方向”的意思。

我们假设上面这个图形的函数是 $y = (x-1)^2+0.001$ ，则 $y’_x = 2(x-1)$ 。

在点B上，这个函数的切线（绿色）是指向下方的（Y轴方向），所以是个负数：假设 $X_B$
= 0.1, 则 $y ’ = 2 * (0.1 - 1) = - 1.8$ 。
在F点上，切线（绿色）向上：假设 $X_F$
= 1.5, 则 $y ’ = 2 * (1.5 - 1) = 1$ ，是个正数。

而在标准的权重更新公式里：

$η*\Delta{w}$

$η*\Delta{b}$

可以看到无论是w还是b，都是用上一次的权重值减去步长 $×\times$ 梯度。注意，我们在上一个例子中，是用b直接加减 $Δb\Delta{b}$ 的，并没有用到η，或者说η=1。这样的问题就是步长可能过大，一下子就跳过了极值点。

当梯度(y’)是正数时，即点F的位置， $x = x - η * 1$ ，切线向上，x值会变小，权重值会从右侧向x=1靠近；
当梯度(y’)是负数时，亦即点B的位置，切线向下，x值会变大：$x = x
η*(-1.8)
= x + η*1.8$，最终运算结果变成了加法，与切线方向相反，权重值会从左侧向x=1靠近。

所以总体上看，无论x在极值的左侧还是右侧，都会向中间（坡底）靠拢，确实是“下降”了。

不知不觉中，我们已经接触到了第一个神经网络中的超参η，即步长值，这个值对于神经网络训练非常重要，决定了训练时间的长短，它的取值一般是从0.1到0.0001，自己选择。

曲线和弦线的关系？

我们先知道了A点的切线的方向，亦即黄色的线，但是不知道长度
我们有步长值η，以及梯度下降公式 $X_1 = X_0 – η * dx$
因为 $yx′的导数dx=2(X−1),η=0.1,X0=0.2,于是有X1=X0–0.1∗2(X0−1)=0.36y'_x的导数dx = 2(X-1), η = 0.1, X_0 = 0.2, 于是有X_1 = X_0–0.1*2(X_0-1) = 0.36$ ，这就等同于我们知道了切线的长度，亦即绿色的线的长度和方向都确定了
然后我们可以画出红色的线（亦即弦线）