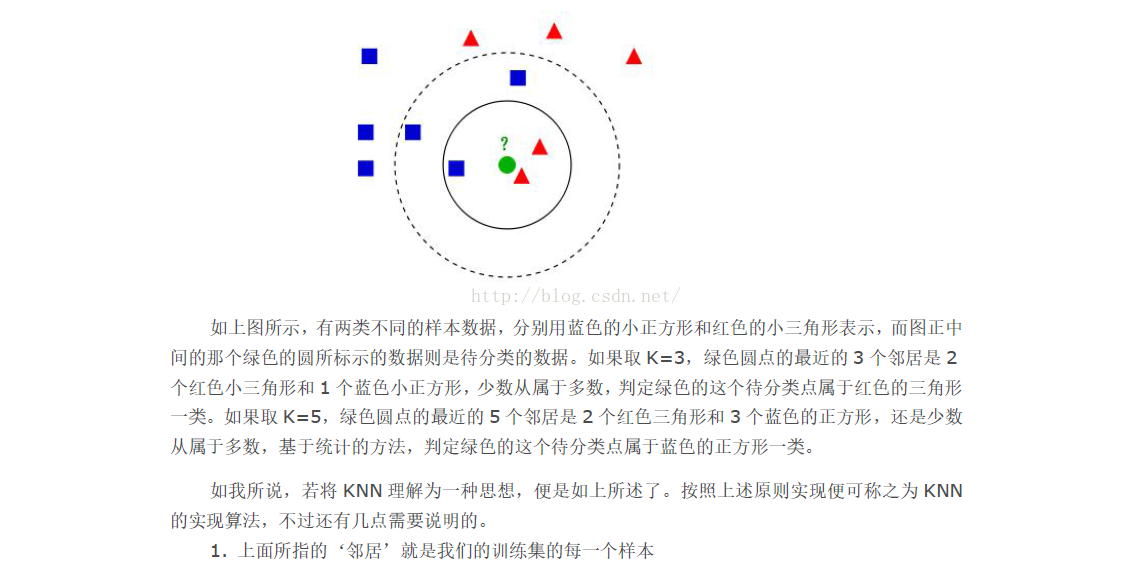
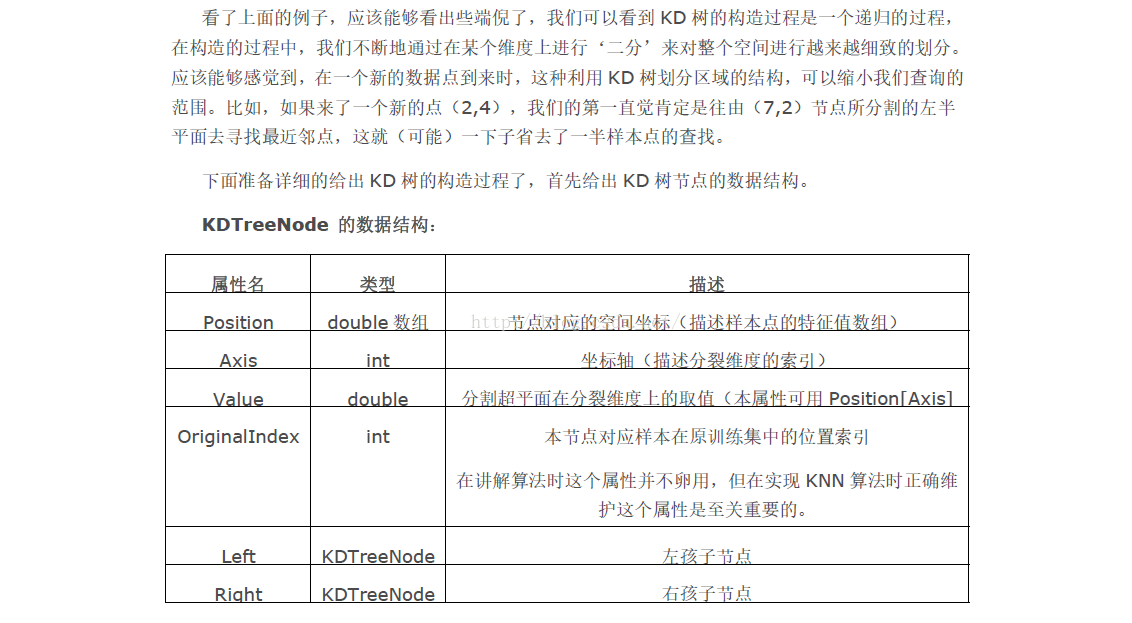
KD树节点

/// <summary>/// ＫＤ树节点/// /2016/4/1安晟添加/// </summary>[Serializable]public class KDTreeNode{/// <summary>///   获取或设置节点的空间坐标/// </summary>public double[] Position { get; set; }/// <summary>///   获取或设置分裂维度的索引///   Gets or sets the dimension index of the split. /// </summary>public int Axis { get; set; }/// <summary>///   获取或设置该节点在分裂维度上的取值/// </summary>public double Value { get; set; }/// <summary>/// 获取或设置该节点对应样本在原数据集中的索引/// 这个属性在查询k近邻元素时十分重要/// </summary>public int OriginalIndex { get; set; }/// <summary>///   获取或设置该节点的左孩子节点/// </summary>public KDTreeNode Left { get; set; }/// <summary>///   获取或设置该节点的右孩子节点/// </summary>public KDTreeNode Right { get; set; }/// <summary>/// 获取该节点是否为叶子节点（木有孩子节点）///   Gets whether this node is a leaf (has no children)./// </summary>public bool IsLeaf{get { return Left == null && Right == null; }}}

构造KD树

/// <summary>/// 构造KDTree/// </summary>/// <param name="DateSet">输入样本集（构造树的过程中样本的顺序会被修改，不过不必担心，/// 方法内部已经单独克隆一块内存区域来处理）</param>public void BuildKDTree(double[][] DataSet){KDTreeNode rootNode = new KDTreeNode();//克隆数据集，DataSet将指向新开辟的数据集//这样expand_kdTreeNode对样本顺序进行修改就不会影响到外部调用者DataSet = (double[][])DataSet.Clone();//Indexs数组用于记录每个样本对应的索引//在expand_kdTreeNode方法内部，Indexs应随着DataSet中样本数据顺序的变化相应的变动。int[] Indexs = new int[DataSet.Length];for (int i = 0; i < DataSet.Length; i++)Indexs[i] = i;//从根节点开始递归构造KD树expand_kdTreeNode(rootNode, DataSet, Indexs, 0, DataSet.Length);this.Root = rootNode;this.Dimensions = DataSet.Length;}

/// <summary>/// 递归增加kd树节点/// 按照方差选择分裂维度/// 内部样本会被打乱顺序，如有需要使用前需单独复制一块内存区域/// </summary>/// <param name="currentNode"></param>/// <param name="DataSet"></param>/// <param name="startIndex"></param>/// <param name="length"></param>private void expand_kdTreeNode(KDTreeNode currentNode,double[][] DataSet,int[] Indexs,int startIndex,int length){if(length==1){//当前只有一个样本点，无需再进行分裂//当前节点为叶子节点currentNode.Position = DataSet[startIndex];currentNode.OriginalIndex = Indexs[startIndex];currentNode.Left = null;currentNode.Right = null;//因为是叶子节点并不需要分裂，所以 分裂维度Axis属性 和 该维度对应值Value属性 随便赋一个值就好了currentNode.Axis = 0;currentNode.Value = currentNode.Position[0];}else{//else对应通常情况，即需要对当前的数据集DataSet[startIndex:startIndex+length-1]//的各个特征维度进行方差分析，找出分裂维度和分裂值，生成当前节点#region 对数据集的关心区域，按照找到的分裂维度进行排序//计算各个维度的方差，找到分裂维度int split = CalculateFeaturesVariance(DataSet, startIndex, length);//根据split维特征的取值，对数据集进行排序double[] splitValueArray = new double[length]; //记录split维的特征值数组int[] IndexArray = new int[length];            //记录对应相对索引（从0开始）for(int i=startIndex;i<startIndex+ length;i++){splitValueArray[i - startIndex] = DataSet[i][split];IndexArray[i - startIndex] = i-startIndex;  }//根据splitValueArray记录的split维的特征值数组，同时对splitValueArray和IndexArray进行排序//IndexArray排序后记录的是 startIndex:startIndex+length-1 排序时的交换顺序Array.Sort(splitValueArray, IndexArray);//根据结果对DataSet的关心区域startIndex:startIndex+length-1重新排序//首先需要克隆关心区域到内存中double[][] tempData = new double[length][];int[] tempIndex = new int[length];for(int i=startIndex;i<startIndex+length;i++){tempData[i - startIndex] = DataSet[i];tempIndex[i - startIndex] = Indexs[i];}int RelativeDataIndex = -1; //对于每一个位置，它应当插入的元素所对应的排序前的索引for (int i = startIndex; i < startIndex + length; i++){RelativeDataIndex = IndexArray[i - startIndex];DataSet[i] = tempData[RelativeDataIndex];Indexs[i] = tempIndex[RelativeDataIndex];}//将临时数组清空，本函数由于是个递归函数，//为了避免内存中可能会存众多的tempData,所以用完就清空掉，应该是合理的tempData = null;tempIndex = null;#endregion//到这里数据集的关心区域已经按照split维进行排序了#region 构造当前节点int middleIndex = startIndex + length / 2;int leftStart = startIndex;int leftlength = middleIndex - leftStart ;int rightStart = middleIndex + 1;int rightlength = startIndex + length - 1 - middleIndex;currentNode.Axis = split;currentNode.Position = DataSet[middleIndex];currentNode.Value = currentNode.Position[split];currentNode.OriginalIndex = Indexs[middleIndex];currentNode.Left = new KDTreeNode();currentNode.Right = new KDTreeNode();#endregion#region 递归//递归左孩子节点if (leftlength > 0)  //因为选取中点时采取的逻辑，这个if语句是不起作用的（leftlength永远都不会等于0），仅仅是为了便于理解代码expand_kdTreeNode(currentNode.Left, DataSet, Indexs, leftStart, leftlength);elsecurrentNode.Left = null;//递归右孩子节点if (rightlength > 0)expand_kdTreeNode(currentNode.Right, DataSet, Indexs, rightStart, rightlength);elsecurrentNode.Right = null;#endregion}}

<div style="text-align: left;"><span style="font-family: Arial, Helvetica, sans-serif;">/// <summary></span></div>        /// 获取给定样本的K个最近邻邻居/// </summary>/// <param name="DataPointX">数据点</param>/// <param name="KNNIndexs">K个最近邻邻居（在原训练样本中）的索引</param>/// <returns>返回K个最近邻邻居对应的样本</returns>public double[][] GetNearestNeighbors(double[] DataPointX, out int[] KNNIndexs){//用于维护K个最近邻节点KDTreeNodeCollection collection = new KDTreeNodeCollection(this.K);//从根节点开始递归寻找K近邻nearest(this.Root, DataPointX, collection);double[][] KNN_points = new double[collection.listNode.Count][]; //记录K近邻邻居对应数据KNNIndexs = new int[collection.listNode.Count]; //K个最近邻邻居（在原训练样本中）的索引for (int k=0;k<collection.listNode.Count;k++){KNN_points[k] = collection.listNode[k].Position;KNNIndexs[k] = collection.listNode[k].OriginalIndex;}return KNN_points;}

/// <summary>///   搜索K近邻邻居/// </summary>private void nearest(KDTreeNode current, double[] position, KDTreeNodeCollection collection){#region 判断当前节点是否是目前的K近邻邻居// 计算当前节点到指定数据点的距离double d = Distance(position, current.Position);//尝试将新得到的节点加入K近邻节点集合//如果比K个邻居中最远的距离还要大就不会被添加进去collection.Add(current, d);#endregion#region 利用深度优先的逻辑进行递归(完成初步搜索和回溯)//通过分裂维度的取值，判断指定数据点在 当前节点所决定的超平面的哪一边//若在左边，则递归左子节点，然后回溯右半平面//若在右边，则递归右子节点，然后回溯左半平面double value = position[current.Axis]; //指定数据点在分裂维度的取值double median = current.Value;         //当前节点在分裂维度的决定分割超平面的取值double u = value - median;             if (u <= 0){//指定数据点在 当前节点决定超平面的左侧//递归直至叶子节点if (current.Left != null)nearest(current.Left, position, collection);//运行到这里说明已经深度优先搜索到了叶子节点//如果从指定点出发，以当前最大距离为半径的超球面与超平面有交割//则回溯右半平面//Math.Abs(u) <= collection.MaxDistance 意味着以当前最大距离为半径能够与分割超平面有交集，需要回溯if (current.Right != null && Math.Abs(u) <= collection.MaxDistance)nearest(current.Right, position, collection);}else{//指定数据点在 当前节点决定超平面的右侧//原理与上面相同if (current.Right != null)nearest(current.Right, position, collection);if (current.Left != null && Math.Abs(u) <= collection.MaxDistance)nearest(current.Left, position, collection);}#endregion}