svm推广到多类情况

一对多的最大响应策略(one against all)
假设有A 、B、C.. D四类样本需要划分。在抽取训练集的时候，分别按照如下4种方式划分。

• A. 所对应的样本特征向量作为正集（类标签为+1), B、C、D所对应的样本特征向量作为负集（类标签为-1).
• B所对应的样本特征向量作为正集，A. C. D所对应的样本特征向量作为负集
• C所对应的样本特征向量作为正集， A. B, D所对应的样本特征向量作为负集．
• D所对应的样本特征向量作为正集， A. B、 C所对应的样本特征向量作为负集．

对上述4个训练集分别进行训练， 得到4个SVM分类器。在测试的时候， 把未知类别的测试样本又分别送入这4个分类器进行判决,取最大值

一对一的投票策略(one against one 叶th voting)
将A. B、C, D四类样本两类两类地组成训练集， 即(A,B)、(A.C)、(A,D)、(B,C)、(B,D)、{C,D), 得到6个（对于n类问题， 为n(n-1)/2个） SVM二分器。在测试的时候，把测试样本又依次送入这6个二分类器， 采取投票形式， 最后得到一组结果。投票是以如下方式进行的。

初始化： vote(A)= vote(B)= vote(C)= vote{D)=O。
投票过程：如果使用训练集(A,B)得到的分类器将f判定为A类，则vote(:A)=vote(A)+ 1 , 否则vote(B)=vote(B)+ 1; 如果使用(A,C)训练的分类器将又判定为A类，则vote(.4.)=vote(A)+ 1, 否则vote(C)=vote(C)+l; . ….. ; 如果使用(C,D)训练的分类器将又判定为C类，则
vote(C)=vote(C)+ 1 , 否则vote(D)=vote(D)+ 1。
最终判决： Max(vote(A), vote(B), vote{C), vote(D))。如有两个以上的最大值， 则一般可简单地取第一个最大值所对应的类别。

3. 一对一的淘汰策略(one against one with. eUmlnating)
这是在文献中专门针对SVM提出的一种多类推广策略，实际上它也适用于所有可以提供分类器置信度信息的二分器。该方法同样基于一对一判别策略解决多类问题， 对于这4类问题， 需训练6个分类器(A,.B)、(A,C)、(A,D）、(B,C)、(B,D)、(C,D)。显然， 对于这4类中的任意一类， 如第A类中的某一样本， 就可由(A,B）、(A,C)、(A,D)这3个二分器中的任意一个来识别，即判别函数间存在冗余。于是我们将这些二分器根据其置信度从大到小排序，置信度越大表示此二分器分类的结果越可靠， 反之则越有可能出现误判。对这6个分类器按其置信度由大到小排序并分别编号， 假设为1 # (A,C), 2# (A,B）， 3#(A,D)., 4# (B,D), 5# (C,D), 6# (B,C) 。

此时， 判别过程如下。
(1) 设被识别对象为X, 首先由1#判别函数进行识别。若判别函数h(x) = +1, 则结果为类型A, 所有关于类型C的判别函数均被淘汰；若判别函数h(x) =-1, 则结果为类型C,所有关于类型A的判别函数均被淘汰；若判别函数h(x) = 0, 为“ 拒绝决策” 的情形， 则直接选用2#判别函数进行识别。
(2)被识别对象x再由4#判别函数进行识别。若结果为类型+1, 淘汰所有关于D类的判别函数， 则所剩判别函数为6# (B,C)。
(3) 被识别对象x再由6#判别函数进行识别。若得到结果为类型+1 则可判定最终的分类结果为B。

那么， 如何来表示置信度呢？对于SVM而言，分割超平面的分类间隔越大，就说明两类样本越容易分开，表明了问题本身较好的可分性。因此可以用各个SVM二分器的分类间隔大小作为其置信度。

SVM的Matlab实现

训练一svmtrain
函数svmtrain用来训练一个SVM分类器， 常用的调用语法为：
SVMStruct = svmtrain(Tranining,Group);
• Training是一个包含训练数据的m行n列的2维矩阵。每行表示1个训练样本（特征 向量），m表示训练样本数目； n表示样本的维数．
• Group是一个代表训练样本类标签的1维向量．其元素值只能为0或1.通常1表示正例，0表示反例.Group的维数必须和Traningg的行数相等，以保证训练样本同其 类别标号的一一对应．
SVMStruct是训练所得的代表SVM分类器的结构体，包含有关最佳分割超平面的种种信息，也可以计算出分类间隔值。

除上述的常用调用形式外，还可通过＜属性名， 属性值＞形式的可选参数设置一些训练相关的高级选项， 从而实现某些自定义功能， 具体说明如下

训练结果的可视化
当训练数据是2维时可利用ShowPlot选项来获得训练结果的可视化解释， 调用形式如下：
svmtrain(…,”ShowPlot”,true);

设定错误代价C
在13.2.2小节讨论非线性可分情况下的C-SVM时， 介绍了错误代价系数C对于训练和分类结果的影响， 下面将给出设定C值的方法。由式(13-21)可知， 引入C对于二次规划问题求解的影响仅仅体现在约束条件当中， 因此通过在调用svmtrain时设置一个优化选项’boxconstraint’即可， 调用形式为：
svmStruct = svmtarin(…,”boxconstraint”,C);
其中， C 为错误代价系数，默认取值为Inf, 表示错分的代价无限大， 分割超平面将倾向于尽可能最小化训练错误。通过适当地设置一个有限的C值， 将得到一个图13.7 Cc)中所示的软超平面。

分类-svmclassify
函数svmclassify的作用是利用训练得到的SVMStruct结构对一组样本进行分类，常用调用形式为：
Group = svmclassify(SVMStruct,sample);
SVMStruct是训练得到的代表SVM分类器的结构体， 由函数svmtrain返回．
Sample是要进行分类的样本矩阵， 每行为1个样本特征向量，总行数等于样本数目，总列数是样本特征的维数，它必须和训练该SVM时使用的样本特征维数相同．Group是一个包含Sample中所有样本分类结果的列向量， 其维数与Sample矩阵的行数相同．

应用实例
svm训练分类鸢尾植物

load fisheriris;
data = [meas(:,1),meas(:,2)];    
groups = ismember(species,'setosa');    [train,test] = crossvalind('holdOut',groups);svmStruct = svmtrain(data(train,:),groups(train),'showplot',true);classes = svmclassify(svmStruct,data(test,:),'showplot',true);nCorrect = sum(classes == groups(test));    
accuracy = nCorrect/length(classes);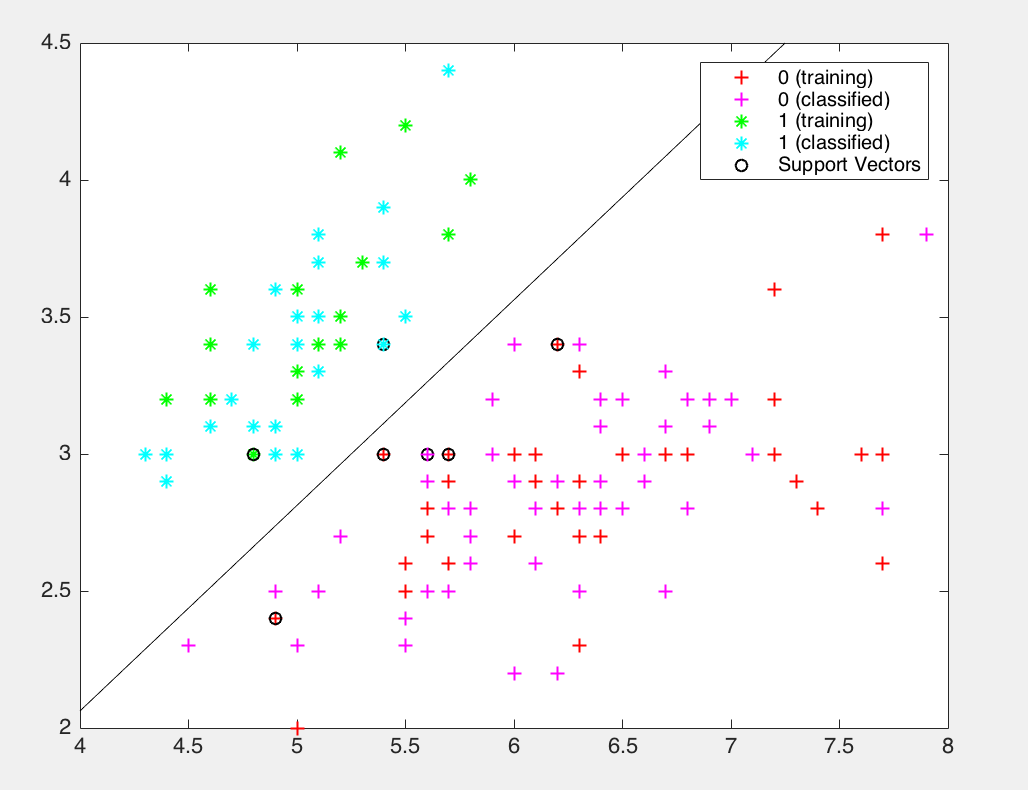

人脸识别

人脸识别简介
人脸识别技术就是以计算机为辅助手段， 从静态图像或动态图像中识别人脸。问题一般可以描述为：给定一个场景的静态或视频图像， 利用已经存储的人脸数据库确认场景中的一个或多个人。一般来说， 人脸识别研究一般分为3个部分： 从具有复杂背景的场景中检测并
分离出人脸所在的区域；抽取人脸识别特征；然后进行匹配和识别

前期处理
实验数据集仍然采用ORI人脸库。由千每幅人脸图像均包括112X92个像素（参见10.4.1小节），巨大的维数打消了我们将每幅图像直接以其像素作为特征(ANN数字字符识别中的做法）的念头。而实际上， 由于原始图像各维像素之间存在着大量的相关性这种做法也是没有必要的。因此需要首先通过主成分分析(PCA)的方法去除相关性， 我们将在1.0.4节那个基于主成份分析(PCA)的人脸特征提取工作的基础上进行本实验，将PCA降维后得到的20维特征向量作为SVM分类的特征。

前期预处理工作的具体步骤如下。
(1) 数据集的分割。
将整个数据集分为两个部分1个训练集和1个测试集。具体地说，我们将每个人的10张面部图像分成两组，前5张放入训练集，另外5张用作测试。这样训练集与测试集各有40x5 = 200个人脸样本。
(2) 读入训练图像。
将每张图像按列存储为1个10304维的行向量。这样400个人共组成一个400x10304的2维矩阵faceContainer, 每行1个人脸样本.. readFeacsO 函数封装了上述功能
(3)利用PCA降维去除像素之间的相关性。

数据规格化 (Scaling)

数据规格化又称数据尺度归一化，是指将特征的某个属性（特征向量的某一维）的取值范围投射到一个特定范围之内，以消除数值型属性因大小范围不一而影响基于距离的分类方法结果的公正性。

数据规格化的必要性
可以毫不夸张地说，Scaling在一个模式识别问题中占据着举足轻重的地位，甚至关系到整个识别系统的成败。然而如此重要的一个环节却往往易被初学者忽视。当您在同一个数据集上应用了相同的分类器却得到远不如他人的结果时，首先请确定是否进行了正确的Scaling。通常进行Scaling 一般有以下两点必要性：
(1)防止那些处在相对较大的数字范围(numeric ranges)的特征压倒那些处在相对较小的数字范围的特征。
(2)避免计算过程中可能会出现的数字问题。

数据规格化方法
(1)最大最小规格化方法。
(2)零均值规格化方法

实现人脸数据的规格化

function [SVFM, lowVec, upVec] = scaling(VecFeaMat, bTest, lRealBVec, uRealBVec)
% Input:  VecFeaMat --- 需要scaling的 m*n 维数据矩阵，每行一个样本特征向量，列数为维数
%         bTest ---  =1：说明是对于测试样本进行scaling，此时必须提供 lRealBVec 和 uRealBVec
%                       的值，此二值应该是在对训练样本 scaling 时得到的
%                    =0：默认值，对训练样本进行 scaling
%         lRealBVec --- n维向量，对训练样本 scaling 时得到的各维的实际下限信息
%         uRealBVec --- n维向量，对训练样本 scaling 时得到的各维的实际上限信息
%
% output: SVFM --- VecFeaMat的 scaling 版本
%         upVec --- 各维特征的上限(只在对训练样本scaling时有意义，bTest = 0)
%         lowVec --- 各维特征的下限(只在对训练样本scaling时有意义，bTest = 0)
if nargin < 2bTest = 0;
end% 缩放目标范围[-1, 1]
lTargB = -1;
uTargB = 1;[m n] = size(VecFeaMat);SVFM = zeros(m, n);if bTestif nargin < 4error('To do scaling on testset, param lRealB and uRealB are needed.');endif nargout > 1error('When do scaling on testset, only one output is supported.');endfor iCol = 1:nif uRealBVec(iCol) == lRealBVec(iCol)SVFM(:, iCol) = uRealBVec(iCol);SVFM(:, iCol) = 0;elseSVFM(:, iCol) = lTargB  +  ( VecFeaMat(:, iCol) - lRealBVec(iCol) ) / ( uRealBVec(iCol)-lRealBVec(iCol) ) * (uTargB-lTargB); % 测试数据的scalingendend
elseupVec = zeros(1, n);lowVec = zeros(1, n);for iCol = 1:nlowVec(iCol) = min( VecFeaMat(:, iCol) );upVec(iCol) = max( VecFeaMat(:, iCol) );if upVec(iCol) == lowVec(iCol)SVFM(:, iCol) = upVec(iCol);SVFM(:, iCol) = 0;elseSVFM(:, iCol) = lTargB  +  ( VecFeaMat(:, iCol) - lowVec(iCol) ) / ( upVec(iCol)-lowVec(iCol) ) * (uTargB-lTargB); % 训练数据的scalingendend
end

核函数的选择
到目前为止， 要送入SVM的数据已经准备就绪， 但在 “ 启动”SVM之前仍有两个问题摆在面前：
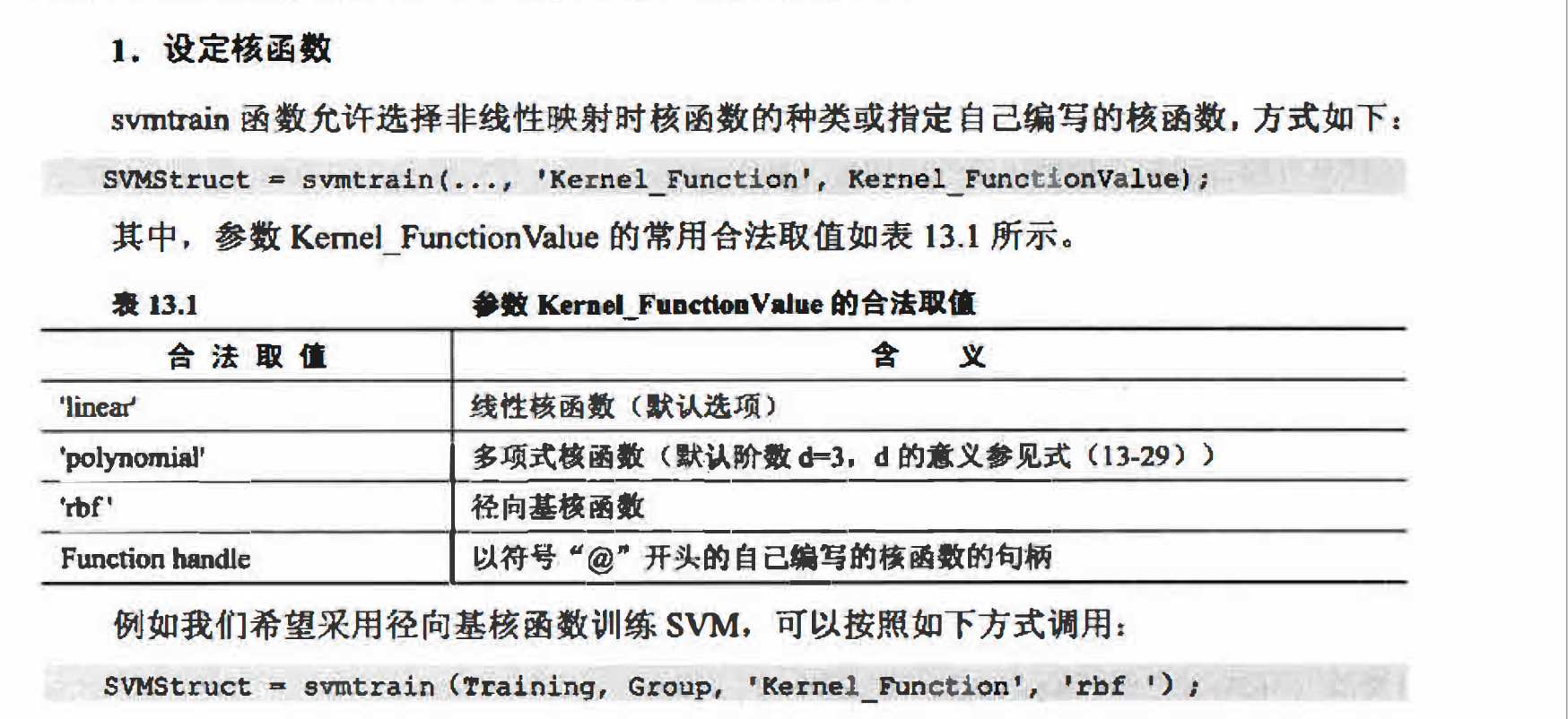
(1)选择哪一种核函数 (Kerne]);
(2)确定核函数的参数以及错误代价系数C的 最佳取值。
下面先来解决第1个问题， 第2个问题留到13.4.5中讨论。由于只有4种常用的核函数（参见13.2.3小节），将它们依次尝试并选择对测试数据效果最好的一个似乎可行， 但后续的参数选择问题将使这成为一个复杂的排列组合问题， 而远 远不是4种可能那么简单。尽管最佳核函数的选择一般与问题自身有关， 但仍有规律可循。 建议初学者在通常情况 下优先考虑径向基核函数RBF

构建多类svm分类器

首先进行训练
在多类SVM训练阶段， 我们要做的就是用n=40类样本构建n(n - 1)/2个SVM二分器，把每个SVM二分器的训练结果(SVMStruct结构体）都保存到一个结构体的细胞数组CASVMStruct中， 具体地说CASVMStruct{ii} {jj}中保存着第ii类与第jj类两类训练得到的
SVMStruct 。最终将多类SVM分类时需要的全部信息保存至结构体multiSVMStruct中返回，可以说multiSVMStruct中包含了我们的训练成果。

function multiSVMStruct = multiSVMTrain(TrainData, nSampPerClass, nClass, C, gamma)
%function multiSVMStruct = multiSVMTrain(TrainData, nSampPerClass, nClass, C, gamma)
% 采用1对1投票策略将 SVM 推广至多类问题的训练过程，将多类SVM训练结果保存至multiSVMStruct中
%
% 输入:--TrainData:每行是一个样本人脸
%     --nClass:人数，即类别数
%     --nSampPerClass:nClass*1维的向量，记录每类的样本数目，如 nSampPerClass(iClass)
%     给出了第iClass类的样本数目
%     --C:错误代价系数，默认为 Inf
%     --gamma:径向基核函数的参数 gamma，默认值为1
%
% 输出:--multiSVMStruct:一个包含多类SVM训练结果的结构体% 默认参数
if nargin < 4C = Inf;gamma = 1;
elseif nargin < 5gamma = 1;
end%开始训练，需要计算每两类间的分类超平面，共(nClass-1)*nClass/2个
for ii=1:(nClass-1)for jj=(ii+1):nClassclear X;clear Y;startPosII = sum( nSampPerClass(1:ii-1) ) + 1;endPosII = startPosII + nSampPerClass(ii) - 1;X(1:nSampPerClass(ii), :) = TrainData(startPosII:endPosII, :);startPosJJ = sum( nSampPerClass(1:jj-1) ) + 1;endPosJJ = startPosJJ + nSampPerClass(jj) - 1;X(nSampPerClass(ii)+1:nSampPerClass(ii)+nSampPerClass(jj), :) = TrainData(startPosJJ:endPosJJ, :);% 设定两两分类时的类标签Y = ones(nSampPerClass(ii) + nSampPerClass(jj), 1);Y(nSampPerClass(ii)+1:nSampPerClass(ii)+nSampPerClass(jj)) = 0;% 第ii个人和第jj个人两两分类时的分类器结构信息CASVMStruct{ii}{jj}= svmtrain( X, Y, 'Kernel_Function', @(X,Y) kfun_rbf(X,Y,gamma), 'boxconstraint', C );end
end% 已学得的分类结果
multiSVMStruct.nClass = nClass;
multiSVMStruct.CASVMStruct = CASVMStruct;% 保存参数
save('Mat/params.mat', 'C', 'gamma');

分类实现
在多类 SVM 分类阶段， 让测试样本依次经过训练得到的 n(n-1)/2 个 (n = 40) 个 SVM 二分器， 通过投票决定其最终类别归属。

function class = multiSVMClassify(TestFace, multiSVMStruct)
% 采用1对1投票策略将 SVM 推广至多类问题的分类过程
% 输入:--TestFace:测试样本集。m*n 的2维矩阵，每行一个测试样本
%     --multiSVMStruct:多类SVM的训练结果，由函数 multiSVMTrain 返回，默认是从Mat/multiSVMTrain.mat文件中读取
%
% 输出:--class: m*1 列向量，对应 TestFace 的类标签% 读入训练结果
if nargin < 2t = dir('Mat/multiSVMTrain.mat');if length(t) == 0error('没有找到训练结果文件，请在分类以前首先进行训练！');endload('Mat/multiSVMTrain.mat');
endnClass = multiSVMStruct.nClass; % 读入类别数
CASVMStruct = multiSVMStruct.CASVMStruct; % 读入两两类之间的分类器信息%%%%%%%%%%%%%%%%%%%%%%%% 投票策略解决多类问题 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
m = size(TestFace, 1);
Voting = zeros(m, nClass); % m个测试样本，每个样本nPerson 个类别的投票箱for iIndex = 1:nClass-1for jIndex = iIndex+1:nClassclasses = svmclassify(CASVMStruct{iIndex}{jIndex}, TestFace);% 投票Voting(:, iIndex) = Voting(:, iIndex) + (classes == 1);Voting(:, jIndex) = Voting(:, jIndex) + (classes == 0);end % for jClass
end % for iClass% final decision by voting result
[vecMaxVal, class] = max( Voting, [], 2 );
%display(sprintf('TestFace对应的类别是:%d',class));

开始训练

function train(C, gamma)
% 整个训练过程，包括读入图像，PCA降维以及多类 SVM 训练，各个阶段的处理结果分别保存至文件：
%   将 PCA 变换矩阵 W 保存至 Mat/PCA.mat
%   将 scaling 的各维上、下界信息保存至 Mat/scaling.mat
%   将 PCA 降维并且 scaling 后的数据保存至 Mat/trainData.mat
%   将多类 SVM 的训练信息保存至 Mat/multiSVMTrain.matglobal imgRow;
global imgCol;display(' ');
display(' ');
display('训练开始...');nPerson=40;
nFacesPerPerson = 5;
display('读入人脸数据...');
[imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson);
display('..............................');nFaces=size(FaceContainer,1);%样本（人脸）数目display('PCA降维...');
[pcaFaces, W] = fastPCA(FaceContainer, 20);% 主成分分析PCA% pcaFaces是200*20的矩阵, 每一行代表一张主成分脸(共40人，每人5张)，每个脸20个维特征
% W是分离变换矩阵, 10304*20 的矩阵
visualize_pc(W);%显示主成分脸
display('..............................');X = pcaFaces;display('Scaling...');
[X,A0,B0] = scaling(X);
save('Mat/scaling.mat', 'A0', 'B0');% 保存 scaling 后的训练数据至 trainData.mat
TrainData = X;
trainLabel = faceLabel;
W = W;
save('Mat/trainData.mat', 'TrainData', 'trainLabel','W');display('..............................');for iPerson = 1:nPersonnSplPerClass(iPerson) = sum( (trainLabel == iPerson) );
endmultiSVMStruct = multiSVMTrain(TrainData, nSplPerClass, nPerson, C, gamma);
display('正在保存训练结果...');
save('Mat/multiSVMTrain.mat', 'multiSVMStruct');
display('..............................');
display('训练结束。');

识别

function nClass = classify(newFacePath)
% 整个分类（识别）过程display(' ');
display(' ');
display('识别开始...');% 读入相关训练结果
display('载入训练参数...');
load('Mat/PCA.mat');
load('Mat/scaling.mat');
load('Mat/trainData.mat');
load('Mat/multiSVMTrain.mat');
display('..............................');xNewFace = ReadAFace(newFacePath); % 读入一个测试样本
xNewFace = double(xNewFace);
% TestFace = (TestFace-repmat(meanVec, m, 1))*V; %其中V是主成分分量，这种才是降维的方法，原代码错了
xNewFace = (xNewFace-repmat(meanVec, 1, 1))*V; % 经过pca变换降维
xNewFace = scaling(xNewFace,1,A0,B0);display('身份识别中...');
nClass = multiSVMClassify(xNewFace);
display('..............................');
display(['身份识别结束，类别为：' num2str(nClass), '。']);

测试

function test()
% 测试对于整个测试集的识别率
%
% 输出：accuracy --- 对于测试集合的识别率display(' ');
display(' ');
display('测试开始...');nFacesPerPerson = 5;
nPerson = 40;
bTest = 1;
% 读入测试集合
display('读入测试集合...');
[imgRow,imgCol,TestFace,testLabel] = ReadFaces(nFacesPerPerson, nPerson, bTest);
display('..............................');% 读入相关训练结果
display('载入训练参数...');
load('Mat/PCA.mat');
load('Mat/scaling.mat');
load('Mat/trainData.mat');
load('Mat/multiSVMTrain.mat');
display('..............................');% PCA降维
display('PCA降维处理...');
[m n] = size(TestFace);
TestFace = (TestFace-repmat(meanVec, m, 1))*V; % 经过pca变换降维
TestFace = scaling(TestFace,1,A0,B0);
display('..............................');% 多类 SVM 分类
display('测试集识别中...');
classes = multiSVMClassify(TestFace);
display('..............................');% 计算识别率
nError = sum(classes ~= testLabel);
accuracy = 1 - nError/length(testLabel);
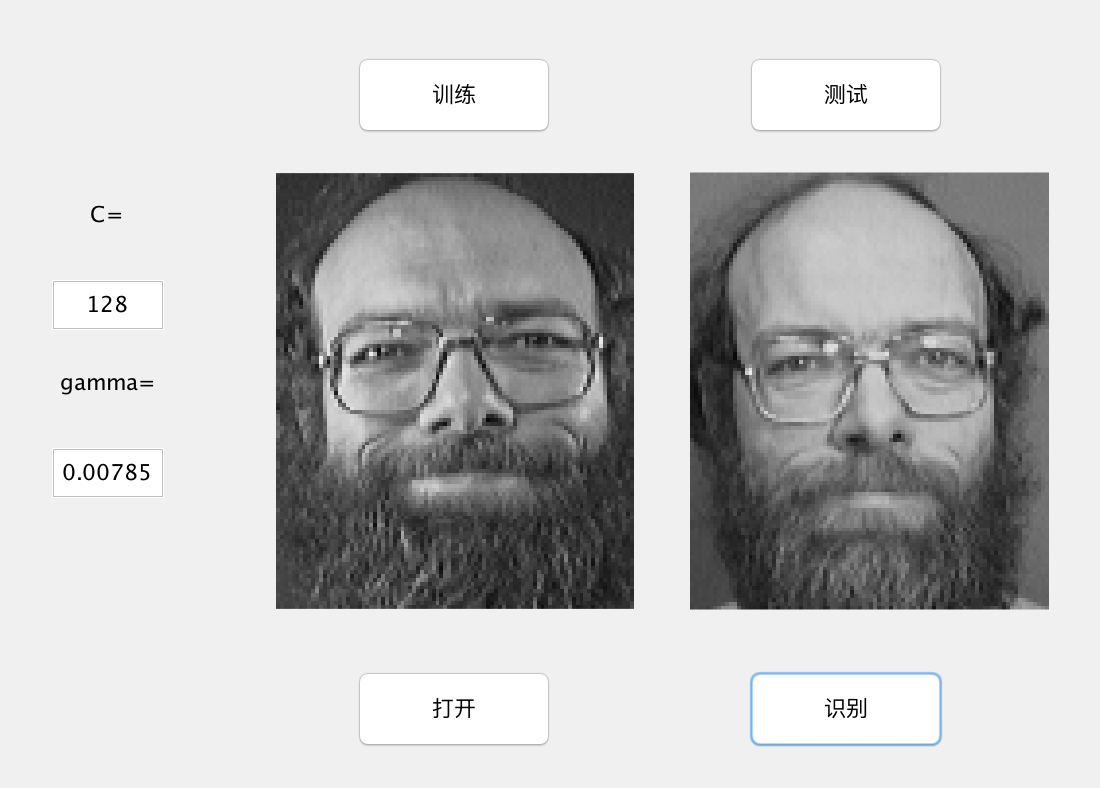
display(['对于测试集200个人脸样本的识别率为', num2str(accuracy*100), '%']);

在C=128,gamma= 0.0785的情况下，准确率大概在81.5%

源码：SourceCode