虽然不是专门研究图像分割的(峰兄才是),但多少接触了一点,并且图像分割是图像处理中的最为复杂的,通过图像分割可以很好地认识图像处理的好多方法。今天看的是边界追踪和链码的表示。网易计算机视觉工程师的第一道选择题就考察了这个,其实冈萨雷斯的书第11章就有讲,还是要多看书啊。
书中是接着图像分割讲的。我们分割完成后总要表示它,那么就有两种思路,一种是选择外部特征,表示分割部分的边界,一种是选择内部特征,找出分割主体的像素。之所以说思路,还没有上升到方法,是因为具体的方法要求描述子要对大小、旋转、平移不敏感。
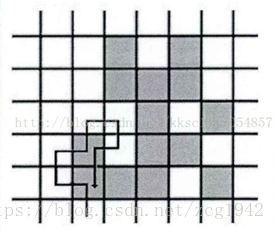
边界追踪就是一种找边界的方法,它的输出是排序过的边界点的序列。追踪方法有Moore边界追踪方法和Square跟踪算法。Moore算法是在当前点的8邻域(摩尔邻域)内顺时针找黑色像素,找到则递归进行下一步。Square则没有利于邻域进行搜索,是一个if-then规则,根据当前像素的情况进行移动方向的选择,如果当前像素是黑色,则左移一个像素;如果当前是白色,则右移。这种方法无法追踪得到只具有八邻接性而不具有四邻接性图形的边界。
边界追踪算法找到了图形边界,我们要对它进行描述和表示,其实就是进行编码。书中主要介绍了Freeman链码,基于Moore边界追踪,对下一个像素相对于当前像素的位置进行编码(有8个方向)。对8个方向依次用0~7的数字表示。就像特战队队员之间通报敌人在几点钟方向一样,链码表示了下一个边界点的方向(远近就是一个像素块的距离,像素的对角线或者边长)。
| 3 | 2 | 1 |
| 4 |
| 0 |
| 5 | 6 | 7 |
Freeman链码显然与初始点的选取有关,我们还需要使编码与初始锚点无关,即无论选择哪一个点做起始点,最后的编码都相同。注意到如果依次使用不同的点做初始点,编码之间的关系是循环移位,于是我们可以对它们进行归一化,选择其中最小的最为最终的编码(把编码看作自然数进行大小的比较)。
刚才提到了,描述子应该具有旋转、平移、缩放不变性。平移不变性很明显是满足的,缩放不变性通过重采样也可以满足。旋转不变性要通过差分编码来解决,同时减少编码长度。需要注意的是计算差值的时候不是对原始的Freeman链码的相邻两个数做减法,而是要满足逆时针关系的条件下做减法,因为在8邻域内编码是按照逆时针的顺序编码的。比如643的差分码。6到4按照逆时针的走法要6步,4到3要7步,所以差分码是67.但是这也只能满足旋转角度是45度的整数倍时的不变性。
链码所能编码的边界应该是离散的,在保持边界特征的前提下尽量短。这就是多边形近似。MPP最小周长多边形近似利用了边界区域像素内外墙之间的凹顶点和凸顶点,利用橡皮条原理完成近似。此外还有聚合技术和分裂技术。
除了链码,表示边界和形状的方法还有标记图和边界线段、骨架。标记图是边界的一维表示,描述质心到边界的距离与角度的关系。为了实现旋转不变性,可以将距离质心最远的点选为起始点,或者在本征轴上选择距离质心最远的点。注意是起始点的意思是角度轴以起始点的角度开始变化。边界线段利用了凸壳和凸缺的概念,从一个凸缺进入另一个凸缺的转折点就是分割点。骨架可以用中轴变换MAT来定义,组成骨架的点是边界上与该点有多个最近邻点的点,可以用燎原之火来形象化:大火从边界开始向中心燃烧,它们集合的地方就是骨架。
边界描述子
讲完表示,就要说到真正的边界描述子了。最简单的是描述边界的长度,偏心率,曲率。长度可以通过链码求出,垂直和水平方向长度是1,对角是根号2.偏心率是长轴和短轴之比,长轴短轴相互垂直,长轴就是直径,是其端点是边界上距离最远的点。曲率描述斜率的变化率。斜率变化非负处的点是凸线段的一部分(其实就是二阶导)。
描述子还有形状数。同样基于链码。形状数的阶n定义为链码的长度(数字个数)。差分链码也可以归一化,得到的就是形状编号。
傅里叶描绘子,将二维平面的点看作复平面的点,坐标看作是一个复数,从而将二维问题简化成一维问题。对它求傅里叶变换,然后就可以重构原来的边界信号。重构过程中可以选择部分分量(舍去高频细节)。同时借助傅里叶变换可以很好地表示选择平移缩放变换。将二维问题转换为一维问题的方法还有统计矩。矩其实是变量与均值的插值的幂的期望。我们可以将曲线旋转作为直方图,这样无论是哪个角度的曲线,都通过将断点连线转至水平方向,即实现了旋转不变性,进一步将直方图归一化为单位面积,直方图转为概率密度图,实现了尺寸的归一化。矩的实现简单,而且矩包含了对边界形状的物理解释。二阶矩是曲线关于均值的扩展程度,三阶矩度量曲线关于均值的对称性。
区域描述子
以上是边界的描述子,对于区域也有对应的一些描述子。比如使用周长和面积表示区域的致密性。圆度率也可以描述致密性,是该区域的面积与同样周长的圆的面积之比。拓扑描绘子,通过孔洞数量H和连通分量的数量C可以定义欧拉数E=C-H.欧拉数同时还可以简单地解释由直线线段表示的区域(多边形网络)。V-Q+F=C-H,V表示顶点数,Q是边数,F是面数。使用连通分量可以在已分割图像中提取最大特征。
区域的另一个特征是纹理。纹理的表示方法又有三种,统计方法、结构方法和频谱方法。
统计方法的对象是灰度直方图,方差表示度量对比度,三阶矩度量直方图偏斜度(负数表示直方图对称尺度向左偏)。直方图中无法体现像素的位置信息,我们通过共生矩阵可以表示灰度值之间的相对位置。共生矩阵其实也是一种统计,只不过统计的是当前像素右边紧邻的像素的灰度值。矩阵的元素m34表示灰度值为3的像素右边第一个元素灰度值是4的情况个数是m。
结构方法的思想是找到一些基本的纹理单元,通过一些规则可以生成复杂的纹理。
频谱方法当然是利用傅里叶频谱,进一步使用极坐标,并且分别对r和角度theta积分,得到两个一维函数。
不变矩
除了纹理,还可以使用不变矩描述区域。大小为MxN的图像的二维(p+q)阶矩定义为:
中心矩还要在求幂之前与均值做差。由二阶矩和三阶矩可以推出7个不变矩组,书中列出了7种不变矩在旋转缩放镜像平移下的表现。
使用主分量进行描绘
有时候我们可以得到多光谱下的图像,即便是单幅图像也可以分成三通道下的三个分量图像。每个像素对应一个多维的向量,于是MxN大小的图像可以得到MxN个向量,向量维数由图像的个数决定。用比较饶但是简洁的说法就是图像的大小决定向量的个数,图像的个数决定向量的大小(维数)。借助霍特林变换(离散KL变换)
A由x的协方差矩阵的特征向量构成。y的协方差矩阵是对角矩阵,主对角线的特征值就是x的协方差矩阵的特征值。可以通过y重构x,当不使用所有的特征值和其对应的特征向量重构时,误差就是剩余没有使用的特征值的和,所以我们霍特林变换是均方误差最小的,因为A的行向量对应的特征值是递减的。霍特林变换也叫主分量变换。
协方差矩阵的最大特征值对应的特征向量指向了总体方差最大的方向,第二个特征向量与第一个垂直,这样就可以找到质心,同时使用主分量变换可以对图像尺度、平移和旋转归一化。
Reference:
- Square:https://blog.csdn.net/kksc1099054857/article/details/74937731
- Freeman:https://blog.csdn.net/yang6464158/article/details/39801381





——形态学图像处理)

——空间滤波)








)





)