形态学来自于生物学,研究动植物的形态和结构。运用在图像中可提取如边界、骨架和凸壳。初学形态学都是在二值化的图像上研究,之后可以扩展到灰度图像。
膨胀和腐蚀
数学形态学与集合论分不开,因为形态学中的操作是基于两个集合的,一个是待处理的像素集合,一个我们叫做结构元SE。SE的形状有多种,原点也有多种,但一般是重心,原点在腐蚀erode和膨胀dilate中表示当前要处理的像素点。像卷积一样,结构元会在图像上遍历,所以我们要对集合A填充,使得结构元的原点在A的边界时,结构元的整体都不会落在图像之外。到现在我们已经知道了形态学基本操作(腐蚀和膨胀)是基本流程和卷积类似,就是利用一个核对像素遍历。卷积是计算卷积核中对应像素乘积之和。腐蚀和膨胀则是基于两个集合的关系。
腐蚀运算的当前像素的结果是两个集合做逻辑与运算,如果SE所占区域和A的一部分是完全重合的,即SE完全属于集合A,那么这一点就取集合A内的值。腐蚀其实是击中击不中变换的简化。击中击不中变换可用于检测图像中目标形状的原点位置,使用的前提条件是图像中的物体之间是断开的,即每个物体被至少一个像素宽的背景像素所环绕。对A和A的补集分别利用D和W-D进行腐蚀,腐蚀结果的交集就是目标的原点。D就是目标,W-D代表与背景相联系的集合。
膨胀是两个集合做或运算,只要部分重合,就把当前像素设置为集合A中的值。膨胀的最简单应用之一是桥接裂缝。而膨胀在连接处细于结构元时会断开。膨胀的一个应用是条件膨胀,可用于孔洞填充,如图像中有一些球体,但是球体中有反光,利用孔洞填充可以消除反光。具体方法是在边界内找到初始点,利用结果元进行迭代,一次迭代是膨胀后与A的补集求交集,交集的目的是寻找背景点。当膨胀之后与A取交集,这时候取的是前景点,可以用于连通分量的提取。
注意我们描述待处理图像A和结构元都是把他们当做集合,膨胀和腐蚀的具体运算也是两个集合之间的关系进行运算,得到的结果也是当做一个集合进行描述。结果的集合是结构元在图中遍历中的所有结果的集合,具体遍历的方式在腐蚀中表现为平移z,在膨胀中表现为结构元的反射(中心对称)的z平移。
还需要注意的是对一幅图(先考虑二值图)中哪些是集合A,我的理解是这个要具体问题具体分析,当结构元元素是白色时,处理的就是图像中的白色区域。
开运算和闭运算
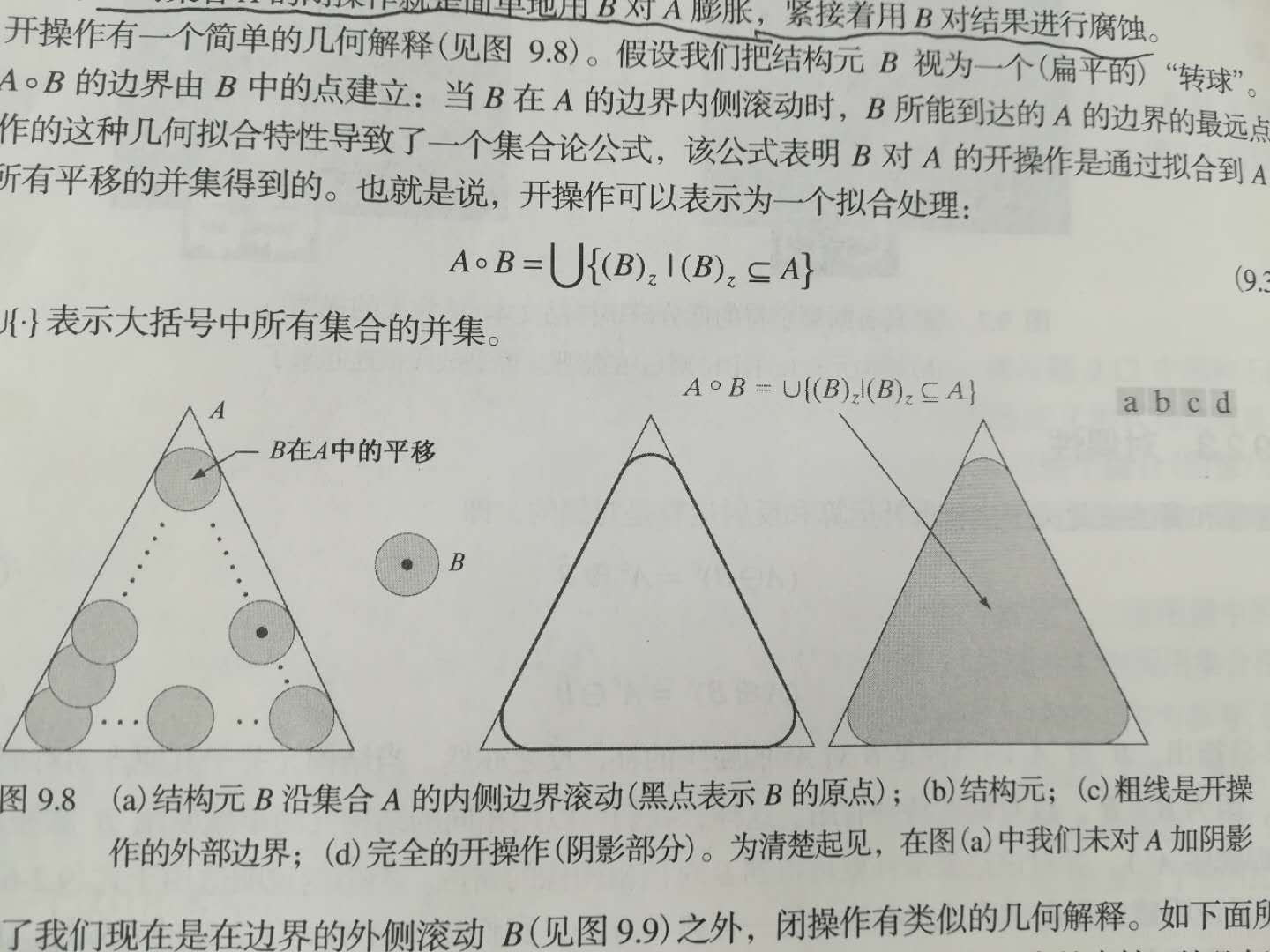
开操作,先腐蚀后膨胀。一个几何解释是开运算是结构元B在A的内侧滚动时所能达覆盖的最大面积。从公式可以看出开运算和腐蚀都是平移后进行条件判断,判断条件是平移之后完全属于集合A,但是结果的操作对象取的不再是结构元的原点,而是平移之后的结构元整体。因为结构体是在A内部平移遍历的,且取的是结构元所能覆盖的面积的最大值,这使得开操作有一个性质:开操作之后的集合是A的子集。开操作同时会断开一些窄的连接和细的突出,可用于消除椒盐噪声。
闭操作和开操作的彼此对偶的。
结构元B对A的闭操作可以看作B的反射对A的补集的开操作,得到的结果再取补集。性质同样对偶,A是闭操作结果的子集。
形态学还可以用于获得集合A的凸壳C(A)。如果A内任意两个点的连线都在A的内部,那么A就是凸集(凸形)。凸壳是包含于A的最小凸集。获得凸集的方法依然是迭代,使用多个结构体对A做击中击不中变换,执行与A的并集,得到的结果再取并集。
根据击中击不中变换,还可以达到细化和粗化。
可以用连续腐蚀和开操作得到骨架。
细化和骨架算法会保留一些寄生分量,因而需要用后处理来消除这些寄生分量。
形态学重建,设计两幅图像和结构元,一幅图像用于标记变换的起始点,一幅图像是模板,用于约束该变换。在形态学重建中,核心是测地膨胀和测地腐蚀。
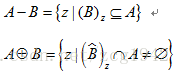


——空间滤波)








)





)


