一．卷积在计算机中实现

1.卷积

将其存入内存当中再操作（按照“行先序”）：

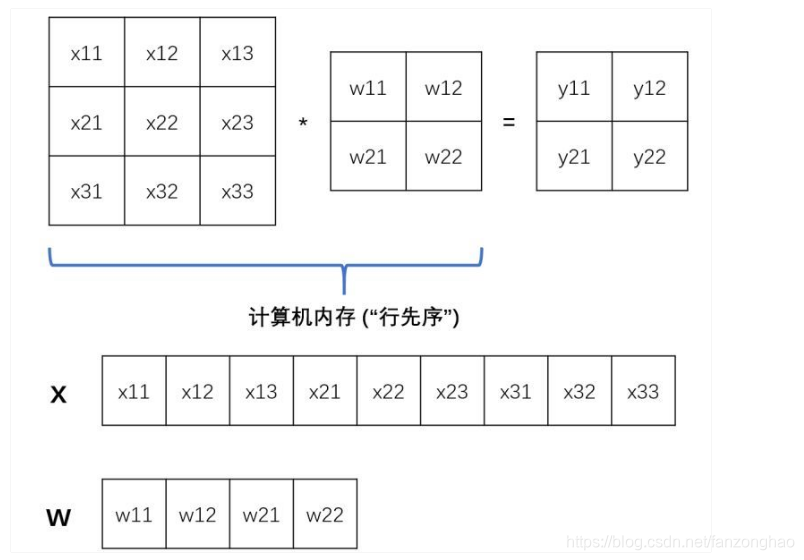
这样就造成混乱．

故需要im2col操作，将特征图转换成庞大的矩阵来进行卷积计算，利用矩阵加速来实现，牺牲了空间．

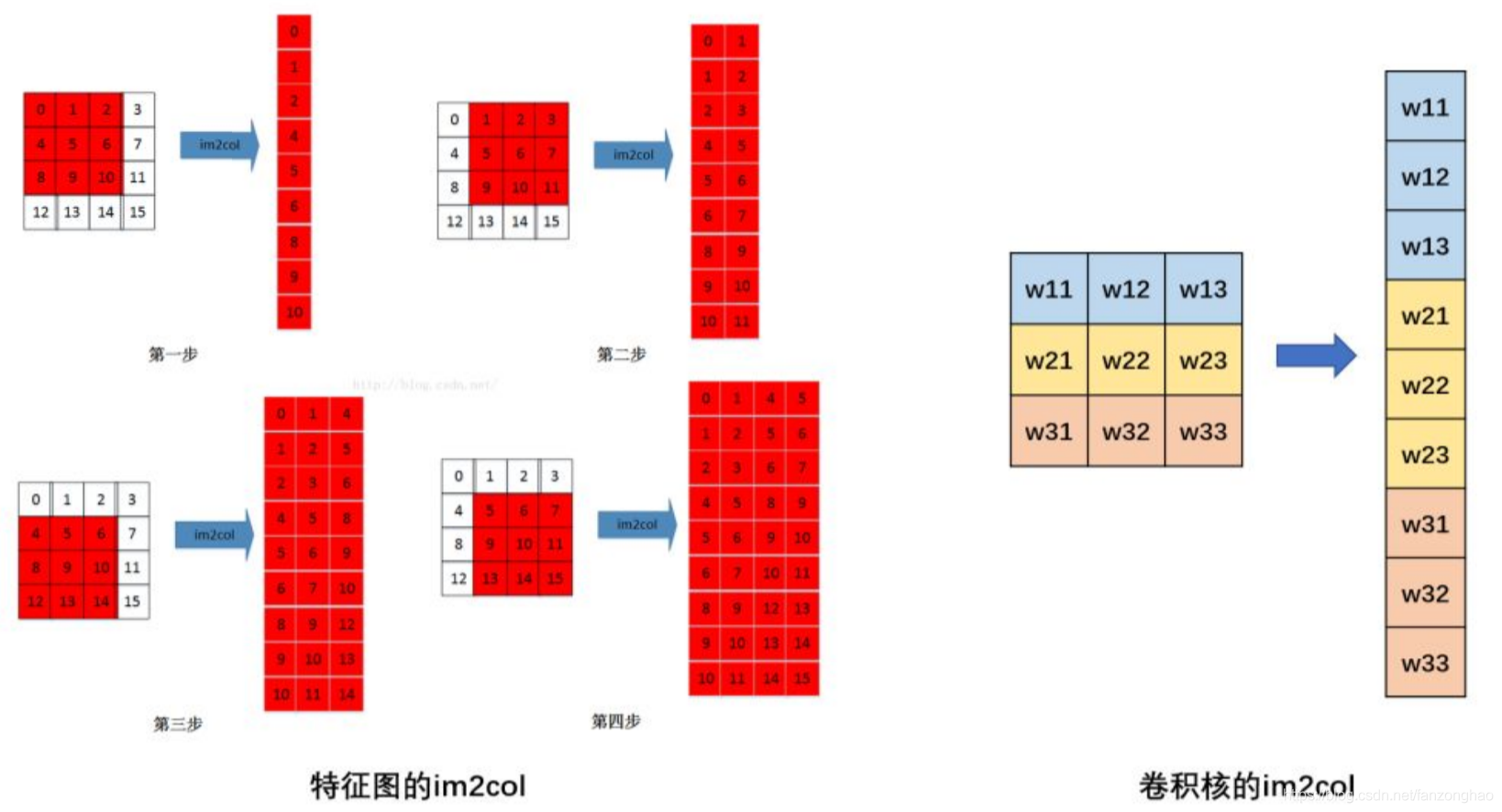
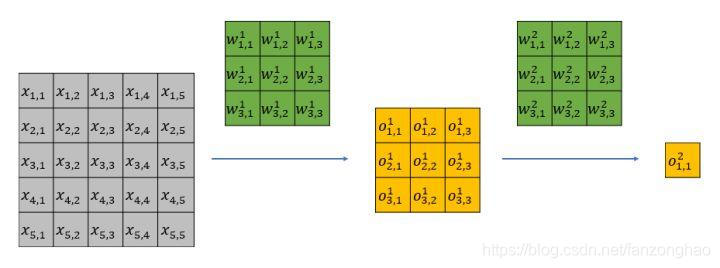
而对于１x１卷积，按照原始储存结构和im2col存储结构计算是一样的，故1x1卷积不需要im2col的过程，所以底层可以有更快的实现，大大节省了数据重排列的时间和空间。如下图所示：

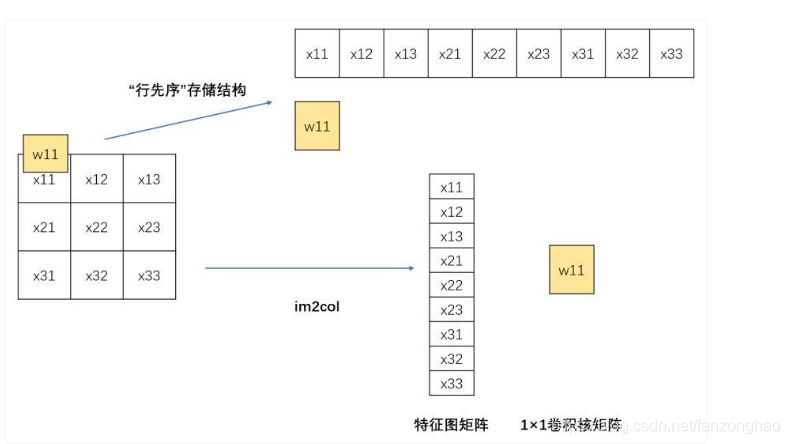
2.反卷积

作用:实现上采样,近似重构图像,卷积可视化

假设输入图像input,为4*4,元素矩阵为：

卷积核kernel尺寸为3*3,，元素矩阵为：

步长stride=1,填充padding=0,则输出图像为(n-k+2*p)/s=2 ，2*2的大小.

将输入图像X拉成一个列向量:

输出图像Y拉成一个列向量:

对于权重矩阵C,则Y=CX

则C为一个稀疏矩阵:

而反卷积就是通过C和Y去求X:

,即可以通过C和Y就可以恢复出X的尺寸.

由此可见反卷积可看为转置卷积.

例子：

     

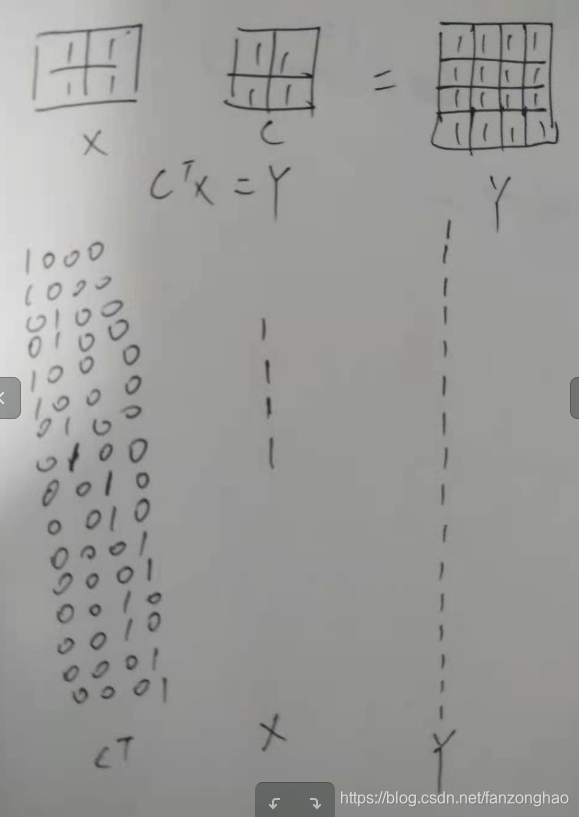
转置卷积缺点:

棋盘效应：

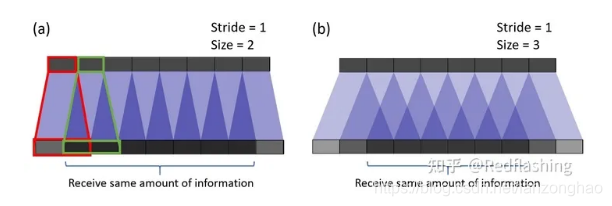
上图可看出，由于转置卷积的不均匀重叠，这是卷积核大小不能被步长整除时，导致出现的。

避免棋盘效应的手段:

（1）.卷积核大小能被步长整除;

（2）.先resize,在卷积。

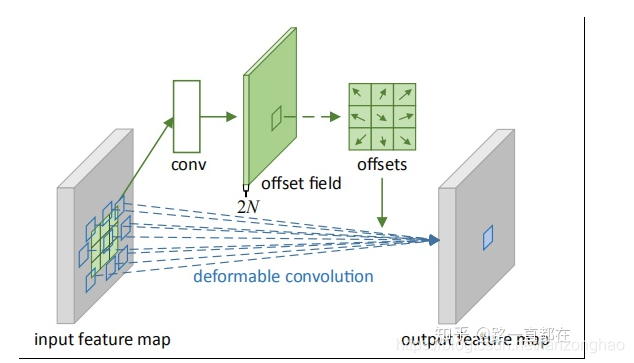
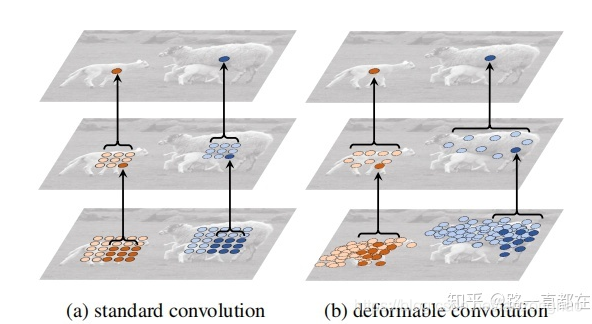
3.可行变卷积(DCN)

通过对feature的每个位置学习一个offset。

流程:

二.pool作用

1.提取对于平移和小变形不变的特征;

2.减少过拟合，提升 泛化能力;

3.减小feature map的尺寸，对于网络具有正则化作用。

三.数据预处理目的

简单的从二维来理解，首先，图像数据是高度相关的，假设其分布如下图a所示(简化为2维)。由于初始化的时候，我们的参数一般都是0均值的，因此开始的拟合y=w*x+b,基本过原点附近(因为b接近于零)，如图b红色虚线。因此，网络需要经过多次学习才能逐步达到如紫色实线的拟合，即收敛的比较慢。如果我们对输入数据先作减均值操作，如图c，显然可以加快学习。更进一步的，我们对数据再进行去相关操作，使得数据更加容易区分，这样又会加快训练，如图d。

四.特征归一化

4.1.目的

特征的单位尺度不一样，比如身高体重，会造成loss函数为椭圆形，而进行了特征归一化就消除了这种单位之间的差异，每一维特征都是平等对待。

4.2.归一化的一些手段

(1)最小最大归一化,归一化到0~1,缺点是有新数据加入导致,max和min有变化。

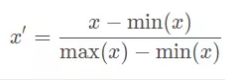
(2)标准归一化，归一化到均值为0，方差为１,其中μ为所有样本数据的均值， δ为所有样本数据的标准差。

(3)将每个样本的特征向量除以其长度，即对样本特征向量的长度进行归一化，长度的度量常使用的是欧氏距离，特点将数据归一化到单位圆上去

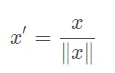
总的来说，归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时，其对解决该问题就有正向作用，反之，就会起反作用。

4.3什么时候需要

与距离计算有关系时就需要，比如梯度下降，而树模型比如决策树，随机森林等只关注当前特征怎么切分更好，与特征间的相对大小无关就不需要。

五.BN

BN可看成在网络的每一层都在做数据预处理．

tensorflow使用BN。

tensorflow中batch normalization的用法_智障变智能-CSDN博客

1,首先我们根据论文来介绍一下BN层的优点:

1）加快训练速度，这样我们就可以使用较大的学习率来训练网络。

2）提高网络的泛化能力。

3）BN层本质上是一个归一化网络层。

4）可以打乱样本训练顺序（这样就不可能出现同一张照片被多次选择用来训练）论文中提到可以提高1%的精度。
问题：深层网络训练过程中，每一层输入随着参数变化而变化，导致每一层都需要适应新的分布，这叫做内部协方差变化。

BN除了解决内部协方差变化，还能起到正则化作用。

BN通过归一化每一层的输入的均值和方差，可以有效解决梯度之间的依赖性。

2,加入γ与β的原因：

由于归一化每一层的输入可能影响该层的代表性，例如sigmoid本来用来做分类要用非线性区域，结果归一化到了线性区域，所以加入上述两个参数，当γ等于样本标准差时，β等于期望时就恢复到了未归一化状态。

3,用minibatch代表整个样本集原因：

当用整个训练集做梯度下降时是不现实的，故采用mini-batch的方式产生均值和方差的估计，通过这种方式的话可以把归一化加入到梯度回传的过程中。注意到这里提及了是计算一个minibatch每一个维度的方差，而不是整个方差。

4,mini-batch算法训练过程：

一个batch-size有m个样本。

输入：输入数据x1…xm（这些数据是准备进入激活函数的数据）
计算过程中可以看到,
1.求数据均值；
2.求数据方差；
3.数据进行归一化
4.训练参数γ，β
5.输出y通过γ与β的线性变换得到新的值
在正向传播的时候，通过可学习的γ与β参数求出新的分布值

在反向传播的时候，通过链式求导方式，求出γ与β以及相关权值。

5.预测过程中的均值和方差：

每层的γ与β两个参数, 通过训练时所得。

每一层均值和方差：

对于均值来说直接计算所有mini-batch均值的期望；然后对于标准偏差采用所有mini-batch σB期望的无偏估计。

6.pytoch 实现

看看pytorch中的实现，BN层的输出Y与输入X之间的关系是：Y = (X - running_mean) / sqrt(running_var + eps) * gamma + beta，而running_mean、running_var则是在前向时先由X计算出mean和var，再由mean和var以动量momentum来更新running_mean和running_var。所以在训练阶段，running_mean和running_var在每次前向时更新一次；在测试阶段，则通过model.eval()固定该BN层的running_mean和running_var，此时这两个值即为训练阶段最后一次前向时确定的值，并在整个测试阶段保持不变。

running_mean = running_mean*(1-momentum)+E[x]*momentum

running_var = running_var*(1-momentum)+Var[x]*momentum

7.SyncBatchNorm 的 PyTorch 实现

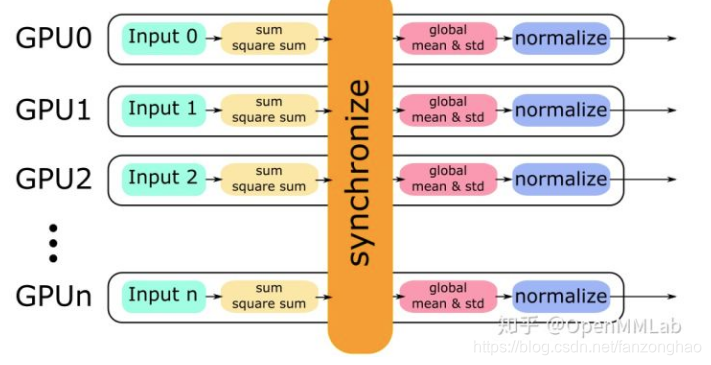
SyncBatchNorm主要用于解决多卡的bn同步问题,

1.每张卡单独计算均值，然后同步，得到全局均值;

2.用全局均值计算每张卡的方差，然后同步即可得到全局方差，但两次会消耗时间挺长，经过下面公式变换就可以一次同步好。

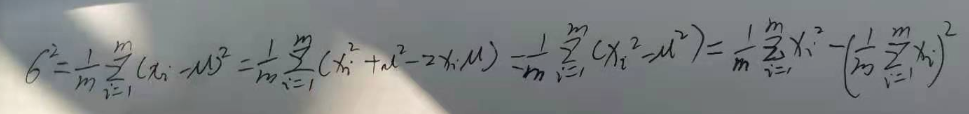
由上图可看出只需要同步计算好和就可以计算全局方差。

8.对于CNN:

如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,f,w,h)，m为min-batch sizes，f为特征图个数，w、h分别为特征图的宽高。在CNN中我们可以把每个特征图看成是一个特征处理（一个神经元），因此在使用Batch Normalization，mini-batch size 的大小就是：m*w*h，于是对于每个特征图都只有一对可学习参数：γ、β。说白了吧，这就是相当于求取所有样本所对应的一个特征图的平均值、方差，然后对这个特征图神经元做归一化。

从上就可以看出BN很受batch的影响,

9.二维数据BN推导:

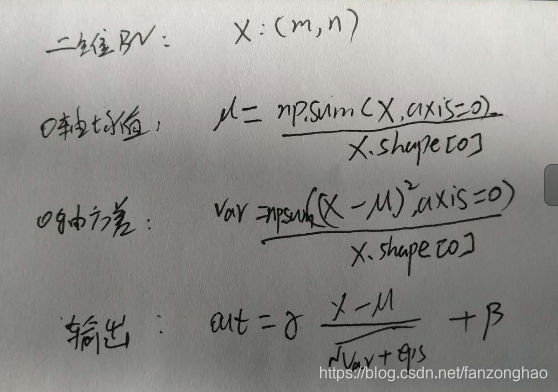
10.另一些归一化手段

由于BN容易受到batch的影响,故又发展出LayerNorm,InstanceNorm,GroupNorm等手段

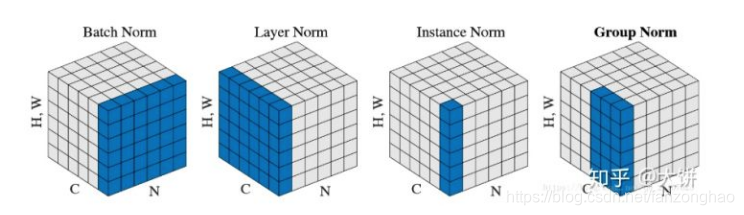
BatchNorm：batch方向做归一化，计算N*H*W的均值,得到C个值,也就是对batch样本中相对应的通道求和除于(H*W)

LayerNorm：channel方向做归一化，计算C*H*W的均值,得到N个值,也就是对batch样本中每个样本求均值,也就是针对单个训练样本进行的，如果不同输入特征不属于相似类别，比如颜色和大小，那么LN的处理就会降低模型的表达能力。Batch Normalization 不适用于变长的网络，如 RNN

InstanceNorm：一个channel内做归一化，计算H*W的均值,得到C*N个值,只利用了空间的信息,也就是对batch样本中单样本的单通道求均值.

GroupNorm：先将channel方向分group，然后每个group内做归一化，计算(C//G)*H*W的均值,得到C//G*N个值,当G==C,就变为IN,当G==1,就变为LN,GN更加适合解决batch小的问题,也就是对batch样本中单样本的C//G个group通道求均值.

11.放在relu之前还是之后？

1、before， conv1-bn1-ReLU1-conv2-bn2-ReLU2

2、after，conv1-ReLU1-bn1-conv2-ReLU2-bn2

１．放在之前:很多网络也是都把bn放到激活前面。所有的激活都是relu，也就是使得负半区的卷积值被抑制，正半区的卷积值被保留。而bn的作用是使得输入值的均值为０，方差为１，也就是说假如relu之前是bn的话，会有接近一半的输入值被抑制，一半的输入值被保留。所以bn放到relu之前的好处可以这样理解：bn可以防止某一层的激活值全部都被抑制，从而防止从这一层往前传的梯度全都变成０，也就是防止梯度消失。（当然也可以防止梯度爆炸.还有一个好处，把bn放到激活前面是有可以把卷积的weight和bn的参数进行合并的，所以它有利于网络在做前向inference时候进行加速。

2.放在之后:before中ReLU1截断了部分bn1归一化以后的数据，所以很有可能归一化的数据已经不再完全满足0均值和单位方差，而after中ReLU1之后的数据做了归一化，归一化后仍满足0均值和单位方差。所以放后边更有效也是可以理解的。

12.推理时卷积与BN融合

官方代码:

import copy
import torchdef fuse_conv_bn_eval(conv, bn):assert(not (conv.training or bn.training)), "Fusion only for eval!"fused_conv = copy.deepcopy(conv)fused_conv.weight, fused_conv.bias = \fuse_conv_bn_weights(fused_conv.weight, fused_conv.bias,bn.running_mean, bn.running_var, bn.eps, bn.weight, bn.bias)return fused_convdef fuse_conv_bn_weights(conv_w, conv_b, bn_rm, bn_rv, bn_eps, bn_w, bn_b):if conv_b is None:conv_b = torch.zeros_like(bn_rm)if bn_w is None:bn_w = torch.ones_like(bn_rm)if bn_b is None:bn_b = torch.zeros_like(bn_rm)bn_var_rsqrt = torch.rsqrt(bn_rv + bn_eps)conv_w = conv_w * (bn_w * bn_var_rsqrt).reshape([-1] + [1] * (len(conv_w.shape) - 1)) # conv_b = (conv_b - bn_rm) * bn_var_rsqrt * bn_w + bn_breturn torch.nn.Parameter(conv_w), torch.nn.Parameter(conv_b)

六.感受野

１．理解

Understanding the Effective Receptive Field in Deep Convolutional Neural Networks

特征的有效感受野（实际起作用的感受野）是远小于理论感受野的

可看出实际的感受野是呈高斯分布的.

感受野中心像素与边缘像素对于梯度的贡献是不一样的.

２．计算

具体如下图：

top往下层层迭代直到追溯回input image，从而计算出RF.

1.感受野计算:

:本层感受野;

:上层感受野;

:第i层卷积或池化的步长

k:本层卷积核大小

2.空洞卷积卷积核计算:K=k+(k-1)(r-1)，k为原始卷积核大小，r为空洞卷积参数空洞率，带入上式即可计算空洞卷积感受野；

感受野计算过程:

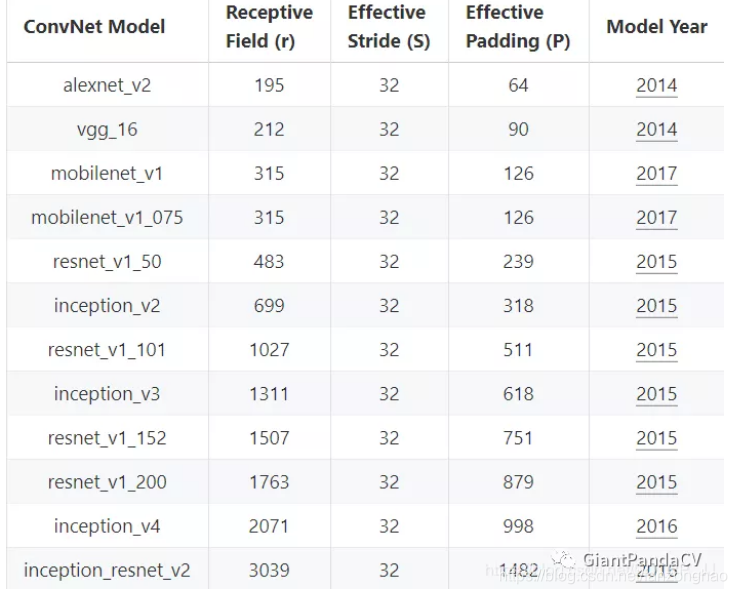
上图是常用分类模型对应的感受野的结果，我们可以发现，随着模型的不断进化，感受野在不增大，在比较新提出的网络中，感受野已经能够覆盖整个输入图像了，这就意味着最终特征图中每个点都会使用到整个图像所有得上下文信息。

一个用来计算感受野的网站：Fomoro Visual Inspection

感受野作用:

1. 目标检测：像SSD、RPN、YOLOv3等都使用了anchor，而anchor的设计正是依据感受野，如果感受野太小，只能观察到局部的特征，不足以得到整个目标的信息。如果感受野过大，则会引入过多噪声和无效信息。Anchor太大或太小均会影响性能。

2. 语义分割：最终预测的像素的感受野越大越好，涉及网络一般也是越深越好，这样才能捕获更多的上下文信息，预测才会更准。

3. 分类任务：图像分类中最后卷积层的感受野要大于输入图像，网络深度越深，感受野越大，性能越好。

计算感受野代码:

from collections import namedtuple
import math
import torch as t
import torch.nn as nnSize = namedtuple('Size', ('w', 'h'))
Vector = namedtuple('Vector', ('x', 'y'))class ReceptiveField(namedtuple('ReceptiveField', ('offset', 'stride', 'rfsize', 'outputsize', 'inputsize'))):"""Contains information of a network's receptive fields (RF).The RF size, stride and offset can be accessed directly,or used to calculate the coordinates of RF rectangles usingthe convenience methods."""def left(self):"""Return left (x) coordinates of the receptive fields."""return t.arange(float(self.outputsize.w)) * self.stride.x + self.offset.xdef top(self):"""Return top (y) coordinates of the receptive fields."""return t.arange(float(self.outputsize.h)) * self.stride.y + self.offset.ydef hcenter(self):"""Return center (x) coordinates of the receptive fields."""return self.left() + self.rfsize.w / 2def vcenter(self):"""Return center (y) coordinates of the receptive fields."""return self.top() + self.rfsize.h / 2def right(self):"""Return right (x) coordinates of the receptive fields."""return self.left() + self.rfsize.wdef bottom(self):"""Return bottom (y) coordinates of the receptive fields."""return self.top() + self.rfsize.hdef rects(self):"""Return a list of rectangles representing the receptive fields of all output elements. Each rectangle is a tuple (x, y, width, height)."""return [(x, y, self.rfsize.w, self.rfsize.h) for x in self.left().numpy() for y in self.top().numpy()]def show(self, image=None, axes=None, show=True):"""Visualize receptive fields using MatPlotLib."""import matplotlib.pyplot as pltimport matplotlib.patches as patchesif image is None:# create a checkerboard image for the backgroundxs = t.arange(self.inputsize.w).unsqueeze(1)ys = t.arange(self.inputsize.h).unsqueeze(0)image = (xs.remainder(8) >= 4) ^ (ys.remainder(8) >= 4)image = image * 128 + 64if axes is None:(fig, axes) = plt.subplots(1)# convert image to numpy and show itif isinstance(image, t.Tensor):image = image.numpy().transpose(-1, -2)axes.imshow(image, cmap='gray', vmin=0, vmax=255)rect_density = self.stride.x * self.stride.y / (self.rfsize.w * self.rfsize.h)rects = self.rects()print('==rects:', rects)for (index, (x, y, w, h)) in enumerate(rects):  # iterate RFs# show center markerprint('==x + w/2, y + w/2:', x + w/2, y + w/2)marker, = axes.plot(x + w/2, y + w/2, marker='x')# show rectangle with some probability, since it's too dense.# also, always show the first and last rectangles for reference.if index == 0 or index == len(rects) - 1 or t.rand(1).item() < rect_density:axes.add_patch(patches.Rectangle((x, y), w, h, facecolor=marker.get_color(), edgecolor='none', alpha=0.5))first = False# set axis limits correctlyaxes.set_xlim(self.left().min().item(), self.right().max().item())axes.set_ylim(self.top().min().item(), self.bottom().max().item())axes.invert_yaxis()if show: plt.show()(x_dim, y_dim) = (-1, -2)  # indexes of spatial dimensions in tensorsdef receptivefield(net, input_shape, device='cpu'):"""Computes the receptive fields for the given network (nn.Module) and input shape, given as a tuple (images, channels, height, width).Returns a ReceptiveField object."""if len(input_shape) < 4:raise ValueError('Input shape must be at least 4-dimensional (N x C x H x W).')# make gradients of some problematic layers pass-throughhooks = []def insert_hook(module):if isinstance(module, (nn.ReLU, nn.BatchNorm2d, nn.MaxPool2d)):hook = _passthrough_gradif isinstance(module, nn.MaxPool2d):hook = _maxpool_passthrough_gradhooks.append(module.register_backward_hook(hook))net.apply(insert_hook)# remember whether the network was in train/eval mode and set to evalmode = net.trainingnet.eval()# compute forward pass to prepare for gradient computationinput = t.ones(input_shape, requires_grad=True, device=device)output = net(input)if output.dim() < 4:raise ValueError('Network is fully connected (output should have at least 4 dimensions: N x C x H x W).')# output feature map sizeoutputsize = Size(output.shape[x_dim], output.shape[y_dim])if outputsize.w < 2 and outputsize.h < 2:  # note: no error if only one dim is singletonraise ValueError('Network output is too small along spatial dimensions (fully connected).')# get receptive field bounding box, to compute its size.# the position of the one-hot output gradient (pos) is stored for later.(x1, x2, y1, y2, pos) = _project_rf(input, output, return_pos=True)rfsize = Size(x2 - x1 + 1, y2 - y1 + 1)# do projection again with one-cell offsets, to calculate stride(x1o, _, _, _) = _project_rf(input, output, offset_x=1)(_, _, y1o, _) = _project_rf(input, output, offset_y=1)stride = Vector(x1o - x1, y1o - y1)if stride.x == 0 and stride.y == 0:  # note: no error if only one dim is singletonraise ValueError('Input tensor is too small relative to network receptive field.')# compute offset between the top-left corner of the receptive field in the# actual input (x1, y1), and the top-left corner obtained by extrapolating# just based on the output position and stride (the negative terms below).offset = Vector(x1 - pos[x_dim] * stride.x, y1 - pos[y_dim] * stride.y)# remove the hooks from the network, and restore training modefor hook in hooks: hook.remove()net.train(mode)# return results in a nicely packed structureinputsize = Size(input_shape[x_dim], input_shape[y_dim])return ReceptiveField(offset, stride, rfsize, outputsize, inputsize)def _project_rf(input, output, offset_x=0, offset_y=0, return_pos=False):"""Project one-hot output gradient, using back-propagation, and return its bounding box at the input."""# create one-hot output gradient tensor, with 1 in the center (spatially)pos = [0] * len(output.shape)  # index 0th batch/channel/etcpos[x_dim] = math.ceil(output.shape[x_dim] / 2) - 1 + offset_xpos[y_dim] = math.ceil(output.shape[y_dim] / 2) - 1 + offset_yout_grad = t.zeros(output.shape)out_grad[tuple(pos)] = 1# clear gradient firstif input.grad is not None:input.grad.zero_()# propagate gradient of one-hot cell to input tensoroutput.backward(gradient=out_grad, retain_graph=True)# keep only the spatial dimensions of the gradient at the input, and binarizein_grad = input.grad[0, 0]is_inside_rf = (in_grad != 0.0)# x and y coordinates of where input gradients are non-zero (i.e., in the receptive field)xs = is_inside_rf.any(dim=y_dim).nonzero()ys = is_inside_rf.any(dim=x_dim).nonzero()if xs.numel() == 0 or ys.numel() == 0:raise ValueError('Could not propagate gradient through network to determine receptive field.')# return bounds of receptive fieldbounds = (xs.min().item(), xs.max().item(), ys.min().item(), ys.max().item())if return_pos:  # optionally, also return position of one-hot output gradientreturn (*bounds, pos)return boundsdef _passthrough_grad(self, grad_input, grad_output):"""Hook to bypass normal gradient computation (of first input only)."""if isinstance(grad_input, tuple) and len(grad_input) > 1:# replace first input's gradient onlyreturn (grad_output[0], *grad_input[1:])else:  # single inputreturn grad_outputdef _maxpool_passthrough_grad(self, grad_input, grad_output):"""Hook to bypass normal gradient computation of nn.MaxPool2d."""assert isinstance(self, nn.MaxPool2d)if self.dilation != 1 and self.dilation != (1, 1):raise ValueError('Dilation != 1 in max pooling not supported.')# backprop through a nn.AvgPool2d with same args as nn.MaxPool2dwith t.enable_grad():                               input = t.ones(grad_input[0].shape, requires_grad=True)output = nn.functional.avg_pool2d(input, self.kernel_size, self.stride, self.padding, self.ceil_mode)return t.autograd.grad(output, input, grad_output[0])def run_test():"""Tests various combinations of inputs and checks that they are correct."""# this is easy to do for convolutions since the RF is known in closed form.# for kw in [1, 2, 3, 5]:  # kernel width#   for sx in [1, 2, 3]:  # stride in x#     for px in [1, 2, 3, 5]:  # padding in x#       (kh, sy, py) = (kw + 1, sx + 1, px + 1)  # kernel/stride/pad in y#       for width in range(kw + sx * 2, kw + 3 * sx + 1):  # enough width#         for height in range(width + 1, width + sy + 1):#           # create convolution and compute its RF#           print('=(kh, kw), (sy, sx), (py, px):', (kh, kw), (sy, sx), (py, px))#           print('== height, width:', height, width)kh, kw = 3, 3sy, sx = 1, 1py,px = 0, 0height, width = 5, 5net = nn.Conv2d(3, 2, (kh, kw), (sy, sx), (py, px))rf = receptivefield(net, (1, 3, height, width))print('Checking: ', rf)assert rf.rfsize.w == kw and rf.rfsize.h == khassert rf.stride.x == sx and rf.stride.y == syassert rf.offset.x == -px and rf.offset.y == -pyrf.show()assert 1 == 0print('Done, all tests passed.')if __name__ == '__main__':run_test()

代码中以5*5图像,3*3,步长为1kernel为例:

x号是感受野中心,由于感受野很密集,这里就主要展示开始框与结束框.

import torchvision
from receptivefield import receptivefield
import torchif __name__ == '__main__':# get standard ResNetnet = torchvision.models.resnet18()print('===net:', net)# ResNet block to compute receptive field forblock = 2# change the forward function to output convolutional features only.# otherwise the output is fully-connected and the receptive field is the whole image.def features_only(self, x):x = self.conv1(x)x = self.bn1(x)x = self.relu(x)x = self.maxpool(x)if block == 0: return xx = self.layer1(x)if block == 1: return xx = self.layer2(x)if block == 2: return xx = self.layer3(x)if block == 3: return xx = self.layer4(x)return xnet.forward = features_only.__get__(net)  # bind methodprint('====net===', net)x = torch.rand(4, 3, 64, 64)y = net(x)# print('==y.shape:', y.shape) #/4 /4, block = 1print('==y.shape:', y.shape)  # /8 /8, block = 2# # compute receptive field for this input shaperf = receptivefield(net, (1, 3, 480, 480))## # print to console, and visualizeprint(rf)rf.show()

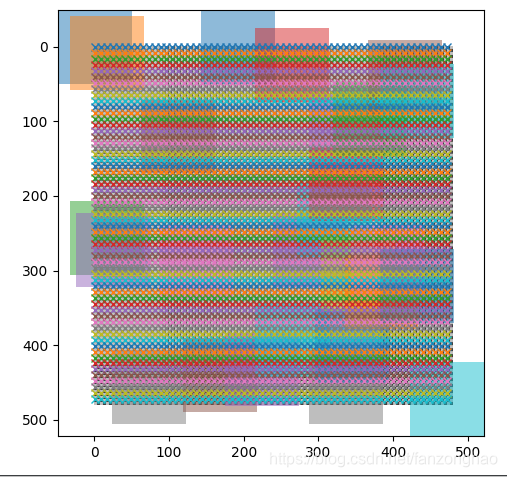
可看出感受野为99.

一些CNN自注意力:

由于卷积核关注的像素太少，故有文献提出，基于预测像素与其他像素之间的协方差，将每个像素视为随机变量。参与的目标像素只是所有像素值的加权和，其中的权值是每个像素与目标像素的相关。

自注意力机制：

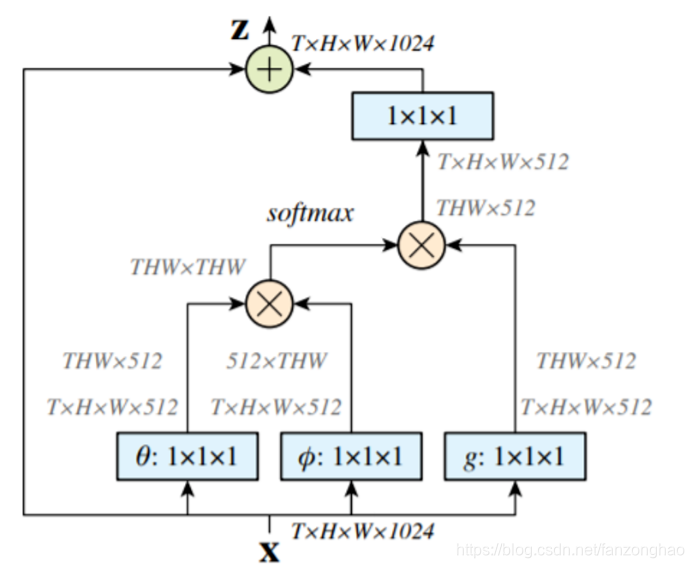
自注意机制 简化版：

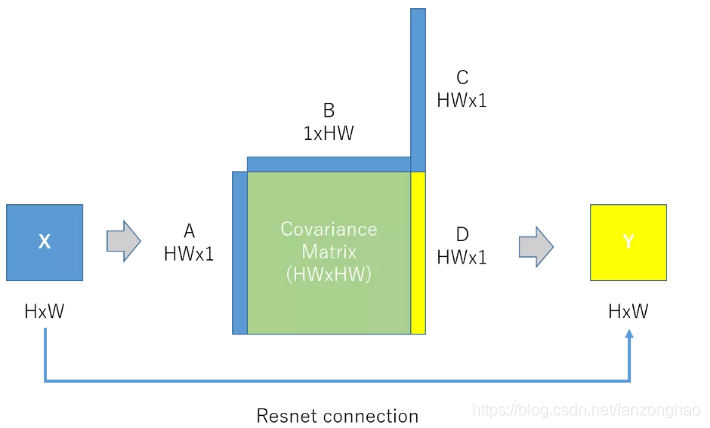
首先输入高度为H、宽度为w的特征图X，然后将X reshape为三个一维向量A、B和C，将A和B相乘得到大小为HWxHW的协方差矩阵。最后，我们用协方差矩阵和C相乘，得到D并对它reshape，得到输出特性图Y，并从输入X进行残差连接。这里D中的每一项都是输入X的加权和，权重是像素和彼此之间的协方差。

故利用自注意力机制，可以在模型训练和预测过程中实现全局参考。

七.梯度回传

1.平均池化梯度回传

平均池化层的前向传播就是把一个patch中的值求取平均来做池化，那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层，这样就保证池化前后的梯度之和保持不变。

2.最大池化梯度回传

最大池化也必须满足梯度之和不变的原则，最大池化的前向传播是把patch中最大的值传递给后一层，而其他像素的值直接被舍弃掉.那么反向传播也就是把梯度直接传给前一层某一个像素，而其他像素不接受梯度，也就是为0。最大池化与平均池化前向传播有一个不同点在于最大池化时需要记录下池化操作时到底哪个像素的值是最大。

3.次梯度回传

例如:Relu在x = 0处的梯度

对于ReLU函数, 当x>0的时候,其导数为1; 当x<0时,其导数为0. 则ReLU函数在x=0的次梯度范围是0到1  ,这里是次梯度有多个,可以取0,1之间的任意值. 工程上为了方便取c=0即可.

八.NMS/soft NMS

1.NMS

代码

每个选出来的Bounding Box检测框（既BBox）用（x,y,h,w, confidence score，Pdog,Pcat）表示，confidence  score表示background和foreground的置信度得分，取值范围[0,1]。Pdog,Pcat分布代表类别是狗和猫的概率。如果是100类的目标检测模型，BBox输出向量为5+100=105。

NMS主要就是通过迭代的形式，不断的以最大得分的框去与其他框做IoU操作，并过滤那些IoU较大（即交集较大）的框。如下图所示NMS的计算过程。

如果是two stage算法，通常在选出BBox有BBox位置(x,y,h,w)和confidence score，没有类别的概率。因为程序是生成BBox，再将选择的BBox的feature map做rescale (一般用ROI pooling)，然后再用分类器分类。NMS一般只能在CPU计算，这也是two stage相对耗时的原因。

但如果是one stage作法，BBox有位置信息(x,y,h,w)、confidence score，以及类别概率，相对于two stage少了后面的rescale和分类程序，所以计算量相对少。

NMS缺点：

1、NMS算法中的最大问题就是它将相邻检测框的分数均强制归零(既将重叠部分大于重叠阈值Nt的检测框移除)。在这种情况下，如果一个真实物体在重叠区域出现（比如人抱着猫），则将导致对该物体的检测失败并降低了算法的平均检测率（average precision, AP）。

2、NMS的阈值也不太容易确定，设置过小会出现误删，设置过高又容易增大误检。

3、NMS一般只能使用CPU计算，无法使用GPU计算。

2.soft NMS

NMS算法是略显粗暴，因为NMS直接将删除所有IoU大于阈值的框。soft-NMS吸取了NMS的教训，在算法执行过程中不是简单的对IoU大于阈值的检测框删除，而是降低得分。算法流程同NMS相同，但是对原置信度得分使用函数运算，目标是降低置信度得分，其IOU越大，得分就下降的越厉害。

参考:

深度学习之17——归一化(BN+LN+IN+GN) - 知乎

反卷积(Transposed Convolution)详细推导 - 知乎

关于感受野的总结 - 简书

你知道如何计算CNN感受野吗？这里有一份详细指南 - 知乎

目标检测和感受野的总结和想法 - 知乎