小孔成像中四个坐标系转换

一.小孔成像基础知识:

1.1透镜成像原理

如图所示：

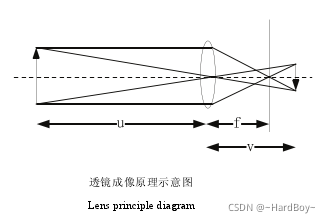
其中 u 为物距， f 为焦距，v 为相距。三者满足关系式：

$1/f = 1/u+1/v$

相机的镜头是一组透镜，当平行于主光轴的光线穿过透镜时，会聚到一点上，这个点叫做焦点，焦点到透镜中心的距离叫做焦距 f。数码相机的镜头相当于一个凸透镜，感光元件就处在这个凸透镜的焦点附近，将焦距近似为凸透镜中心到感光元件的距离时就成为小孔成像模型。小孔成像模型如图所示。

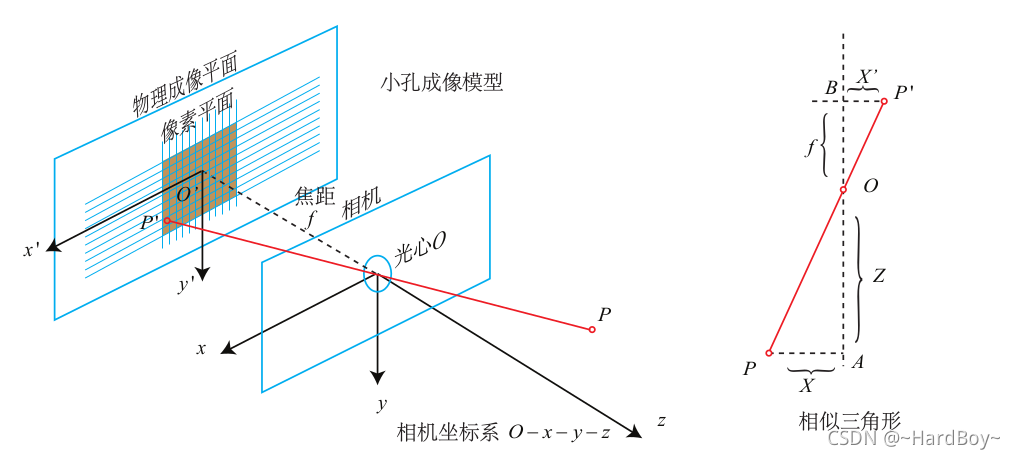
为了计算方便一般采用对称成像平面来进行计算．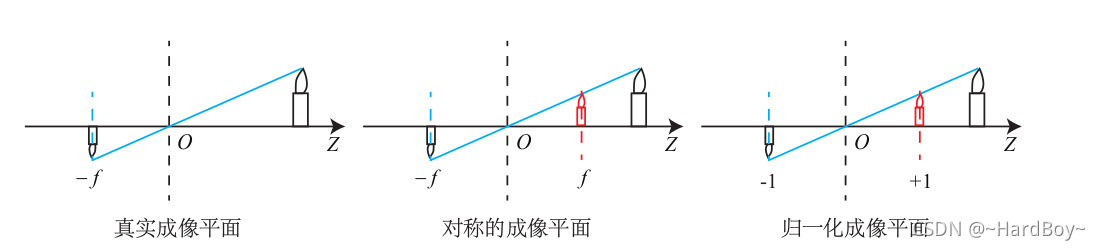

二．四个坐标系转换

2.1 背景

世界坐标系，相机坐标系，图像坐标系，像素坐标系如下图所示：

1：世界坐标系：根据情况而定，可以表示任何物体，此时是由于相机而引入的。单位m。

2：相机坐标系：以摄像机光心为原点（在针孔模型中也就是针孔为光心），z轴与光轴重合也就是z轴指向相机的前方（也就是与成像平面垂直），x轴与y轴的正方向与物体坐标系平行，其中上图中的f为摄像机的焦距。单位m

3：图像物理坐标系（也叫平面坐标系）：用物理单位表示像素的位置，坐标原点为摄像机光轴与图像物理坐标系的交点位置。坐标系为图上o-xy。单位是mm。单位毫米的原因是此时由于相机内部的CCD传感器是很小的，比如8mm x 6mm。但是最后图像照片是也像素为单位比如640x480.这就涉及到了图像物理坐标系与像素坐标系的变换了。

4：像素坐标系：以像素为单位，坐标原点在左上角。这也是一些opencv，OpenGL等库的坐标原点选在左上角的原因。当然明显看出CCD传感器以mm单位到像素中间有转换的。举个例子，CCD传感上上面的8mm x 6mm，转换到像素大小是640x480. 假如dx表示像素坐标系中每个像素的物理大小就是1/80. 也就是说毫米与像素点的之间关系是piexl/mm.

2.2世界坐标系到相机坐标系

物体之间的坐标系变换都可以表示坐标系的旋转变换加上平移变换，则世界坐标系到相机坐标系的转换关系也是如此。绕着不同的轴旋转不同的角度得到不同的旋转矩阵。如下：

那么从世界坐标系到相机坐标系的转换关系如下所示：

2.3相机坐标系到图像坐标系

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

此时投影点p的单位还是mm，并不是pixel，需要进一步转换到像素坐标系。

2.4图像坐标系到像素坐标系

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm.

那么通过上面四个坐标系的转换就可以得到一个点从世界坐标系如何转换到像素坐标系的