来源：孙天任算数学苑

素数的分布密度为 ρ(x)~1/ln(x)，从而在 x 以内的素数个数——通常用 π(x) 表示——为： 
π(x) ~ Li(x) 
其中 Li(x) ≡ ∫ 1/ln(x) dx 是对数积分函数 。这个结果有些读者可能也认出来了，它正是著名的素数定理。
……
素数定理是简洁而优美的，但它对于素数分布的描述仍然是比较粗略的，它给出的只是素数分布的一个渐近形式——即小于 N 的素数个数在 N 趋于无穷时的分布形式。从有关素数分布与素数定理的图示（如下图）中我们也可以看到，π(x) 与 Li(x) 之间是有偏差的， 而且这种偏差的绝对值随着 x 的增加似有持续增加的趋势。

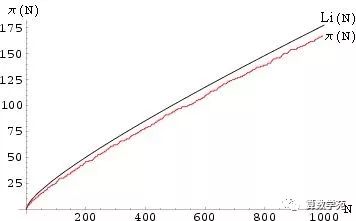
从素数分布与素数定理的图示以及从大范围的计算中人们都发现  Li(x)-π(x) 大于零， 这使得有人猜测 Li(x) 不仅是素数分布的渐近形式， 而且还是其严格上界，  即 Li(x)-π(x) 恒大于零。 这种猜测在 1914 年被英国数学家 John Littlewood  (1885-1977) 所推翻， Littlewood 证明了 Li(x)-π(x) 是一个在正与负之间振荡无穷多次的函数。
……
对于迄今所有被验证过的情形，Li(x)-π(x)>0 都成立，但 Littlewood 却运用分析的力量，不仅证明它不成立，而且证明了它会被违反无穷多次！那么所有验证过的情形说明什么呢？说明虽然有无穷多个 x 违反 Li(x)-π(x)>0，但其中哪怕最小的 x也大得异乎寻常。事实上，我们直到今天也不知道这个最小的 x 究竟有多大，目前对它的估计约为。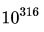  

注：这个最小的 x 被 Hardy 称为 Skewes 数 (Skewes' number)，因为最早对它进行数值估计的是 Littlewood 的学生、 南非数学家 Stanley Skewes (1899–1988）。