这里以 2D Michalewicz function 为对象来演示粒子群算法。

1、Michalewicz function

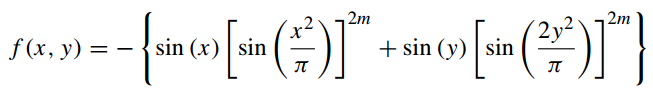
2、代码详解

2.1 画Michalewicz函数的网格图形

f=@(x,y)(-sin(x).*(sin(x.^2/3.1415926)).^(2*m)...-sin(y).*(sin(2*y.^2/3.1415926)).^(2*m));range=[0 4 0 4];
Ngrid=100;
dx=(range(2)-range(1))/Ngrid;
dy=(range(4)-range(3))/Ngrid;
xgrid=range(1):dx:range(2);
ygrid=range(3):dy:range(4);
[x,y]=meshgrid(xgrid,ygrid);
z=f(x,y);
figure(1);
%subplot(1,2,1);
surfc(x,y,z);
hold on;

2.2 粒子群优化算法的子函数

粒子群初始化

function [xn,yn]=init_pso(n,range)
xrange=range(2)-range(1);
yrange=range(4)-range(3);
xn=rand(1,n)*xrange+range(1);
yn=rand(1,n)*yrange+range(3);
end

粒子群的移动

function [xn,yn]=pso_move(xn,yn,xo,yo,a,b,range)
nn=size(yn,2);
xn=xn.*(1-b)+xo.*b+a.*(rand(1,nn)-0.5);
yn=yn.*(1-b)+yo.*b+a.*(rand(1,nn)-0.5);
[xn,yn]=findrange(xn,yn,range);
end

确保粒子群不会出界

function [xn,yn]=findrange(xn,yn,range)
nn=length(yn);
for i=1:nnif xn(i)<=range(1)xn(i)=range(1);endif xn(i)>=range(2)xn(i)=range(2);endif xn(i)<=range(3)xn(i)=range(3);endif xn(i)>=range(4)xn(i)=range(4);end
end
end   

2.3 粒子群算法的主体函数

%n = number of particles
% Num_iterations = number of iterations
n=10;
Num_iterations =50;
best=zeros(Num_iterations,3);
[xn, yn]=init_pso(n,range);
figure(2);
for i = 1:Num_iterationscontour(x,y,z,15); %show the contour of the objectvie functionhold on;%find the current best location(xo,yo)zn=f(xn,yn);zn_min=min(zn);xo=min(xn(zn==zn_min));yo=min(yn(zn==zn_min));zo=min(zn(zn==zn_min));plot(xn,yn,'.',xo,yo,'*');axis(range);beta=0.5;gamma=0.7;alpha=gamma.^i;[xn,yn]=pso_move(xn,yn,xo,yo,alpha,beta,range);drawnow;hold off;best(i,1)=xo;best(i,2)=yo;best(i,3)=zo;
end

3 图形展示，粒子数设为10，迭代次数设为50

Michalewicz function的网格图

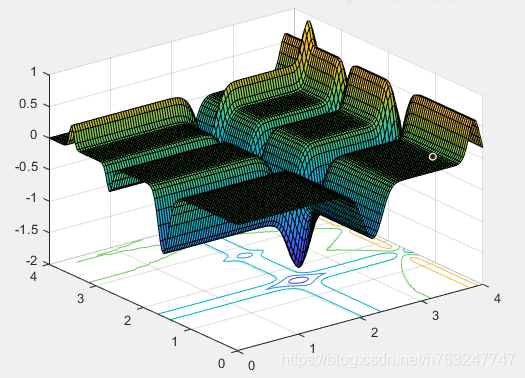
粒子群初始化图，‘点’表示粒子，‘星’表示群中最小的粒子

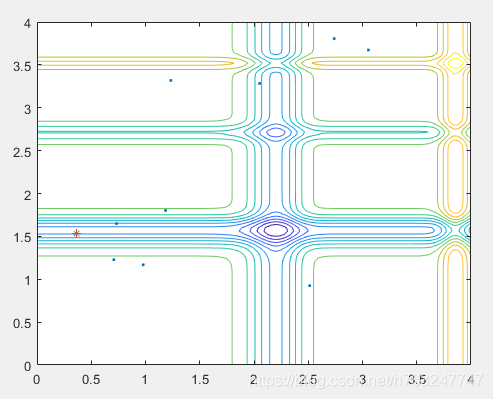
 粒子群运动结束图，最后粒子都运动到了 '星' 点处

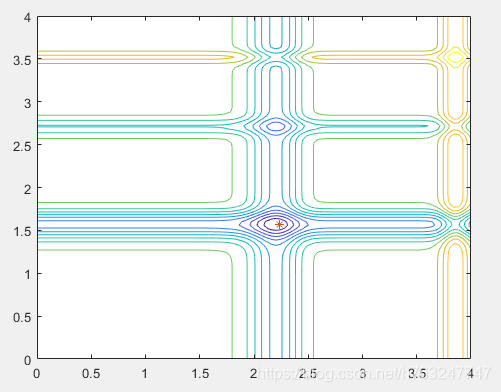
4 粒子群优化算法的优缺点

粒子群优化算法应用范围广，不要求目标函数可导。如果粒子群不够大（比如把粒子数设为2），迭代次数不够多（迭代次数设为5），最后可能无法得到最优解。由于算法初始化时随机生成粒子群，多次运行，粒子群不一样，最终的结果也可能会不一样（进入不同的局部最优解）。