一、图像的傅里叶变换
目的与用途
图像变换的目的：
- 使得图像处理问题简化；
- 有利于图像特征提取；（我们知道特征提取的目的是为了对影像进行分析，根据特征从影像中提取目标等有用信息，特征提取对影像中提取目标非常重要）
- 有助于从概念上增强对图像信息的理解。
图像变换其实就是对图像的另一种表达，正如我们可以将一个函数分解表示为奇偶函数等一系列不同系数的正交函数和等多种方式一样。图像变换通常采用的是一种二维正交变换。其一般要求如下：
- 正交变换必须是可逆的；
- 正变换和反变换的算法不能太复杂；
- 正交变换的特点是变换域中图像将集中分布在低频率成分上，边缘、线状信息反映在高频率成分上，有利于图像处理。
傅里叶变换：将空间域转换为频率域的变换。
任一函数都可以展成三角函数的无穷级数，任何周期函数都可以表示为不同频率的正弦和余弦和的形式，每个正弦和余弦乘以不同的系数（即傅里叶级数展开）。
定义：如果一个周期为T的函数在[-T/2,T/2]满足狄利克雷条件，则在[-T/2,T/2]可以将函数f(t)展开为无穷个正交三角函数的和，如下所示：周期为大写T函数f(t)被展开表示成了无穷多个不同频率的三角函数的加权和，an和bn即为权重系数。
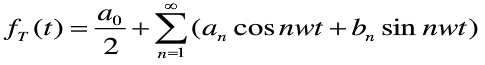
依据欧拉公式
，上面的三角函数形式可以转换成复数形式
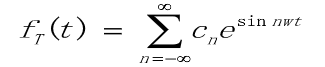
其中，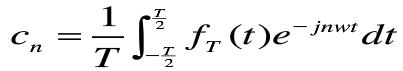
每个nw就代表一个频率分量，不同的n代表不同的频率，Cn为每个频率分量的系数，代表各频率分量的权重。可见，傅里叶级数清楚的表明了信号由哪些频率分量组成及其所占的比重，从而有利于度信号进行分析和处理。
通过上述分析，可将傅里叶变换形象地比作一个玻璃棱镜，可将光分解成不同颜色的物理仪器，每个成分的颜色由波长（或频率）来决定
傅里叶变换可以看成数学上的棱镜，将函数基于频率分解成不同的成分，使得我们能通过频率成分来分析一个函数。
2.连续函数的傅里叶变换
图像作为一个特殊的二维空间信号，可以看成是一维信号的组合，故我们首先来认识以为傅里叶变换及其反变换。
- 一维连续傅里叶变换及其反变换
另f(x）为实变量x的连续函数，f(x)的傅里叶变换F(u）表示，则其定义为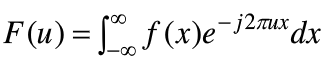
若已知F(u),则傅里叶反变换为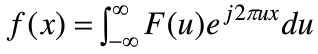
以上两个公式称为傅里叶变换对。
一般情况下，实际信号f(x)是实函数，它的傅里叶变换F(u)通常是复函数。故，F(u)可以表示成实部和虚部的形式或者振幅与相位的形式，以及通过F(u）来表示信号的能量，同样根据欧拉公式
具体表示如下：
傅里叶变换出现的变量u通常称为频率变量。
- 二维连续函数的傅里叶变换
一维傅里叶变换很容易推广到二维的情况，如果f(x,y)是连续可积的 且F(u,v)是可积的，则二维傅里叶变换对为：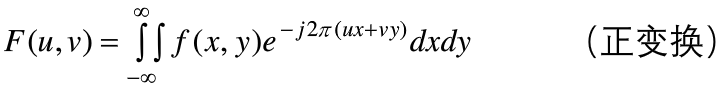
二维函数的傅里叶变换的幅度、相位和能量谱分别为
连续信号可以等间隔抽样进行处理，这样便于计算机处理。
这里我们可以用f(n)的长度为N,则离散信号的傅里叶变换定义式为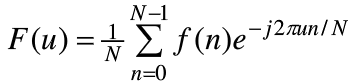
式中u=0,1,2,...,N-1。反变换为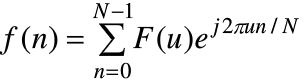
，式中n=0,1,2,...N-1
二维离散函数的傅里叶变换
在二维离散的情况下，比如大小为M*N的图像信号f(m,n)的傅里叶变换对表示为
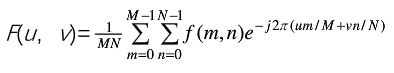，式中u=0,1,2,...,M-1;v=0,1,2,...,N-1。
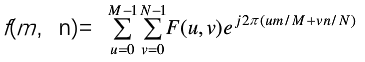,式中m=0,1,2,...,M-1;n=0,1,2,...,N-1。
这里的u,v是频率变量，m和n是空间变量。
一般来说，对一幅图像进行傅里叶变换运算量很大，特别是对大幅面的遥感影像，不直接采用以上公式计算，而是采用快速傅里叶变换算法（FFT）,快速傅里叶变换大大减少了计算量，通过软件编程或者专门的硬件来实现。也是傅里叶变换得到更广泛应用的原因之一。
从二维傅里叶变换的定义式知道，一个M行N列的二维图像的傅里叶变换结果也是一个M*N大小的二维矩阵，与原空间域图像像素坐标对应，频率域图像的左上角坐标也为（0,0），该坐标处的值F(0,0)根据傅里叶变换的定义式可以得到，F(0,0)表示，
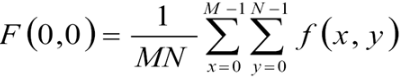这说明：假设f(x,y)是一幅图像，在原点的傅里叶变换等于图像的平均灰度级。
因此，傅里叶变换的原点值反映了图像的平均灰度，即平时信号理论中所说的直流分量。
3.二维离散傅里叶变换的性质
1.可分离性
二维离散傅里叶变换DFT可分离性的基本思想是二维DFT可分离为两次一维DFT。
用通过计算两次一维的FFT来得到二维快速傅里叶变换FFT算法。根据快速傅里叶变换的计算要求，需要图像的行列数均满足2的n次，如果不满足，在计算FFT之前先要对图像补零以满足2的n次。
一个M行N列的二维图像f(x,y),先按照行对列变量y做一次长度为N的一维离散傅里叶变换，再将计算结果按列向对变量x做一次长度为M傅里叶变换就可以得到该图像的傅里叶变换结果，如下式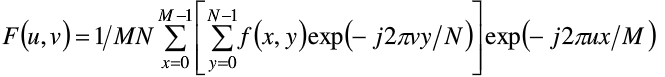
将上式分解开就是如下两个部分，首先得到F(x,v)再由F(x,v)得到F(u,v):
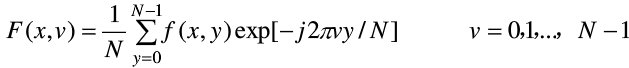
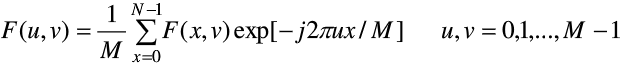
