1.图像的数学变换
空间域:图像的代数运算和几何运算都是利用对输入图像进行加工而得到输出图像
转换空间:最典型的有离散傅里叶变换将原定义在图像空间的图像以某种形式转换到另外一些空间,并利用输入图像在这些空间的特有性质有效而快速地对图像进行处理和分析。
2.图像的像素级的运算
点运算:线性点运算、非线性点运算
代数运算:加、减、乘、除
逻辑运算:求反、异或、或、与
3.图像的空域变换:几何变换、非几何变换:直方图变换
点运算的定义:设输入图像的灰度为f(x,y),输出图像的灰度为g(x,y),则点运算可以表示为
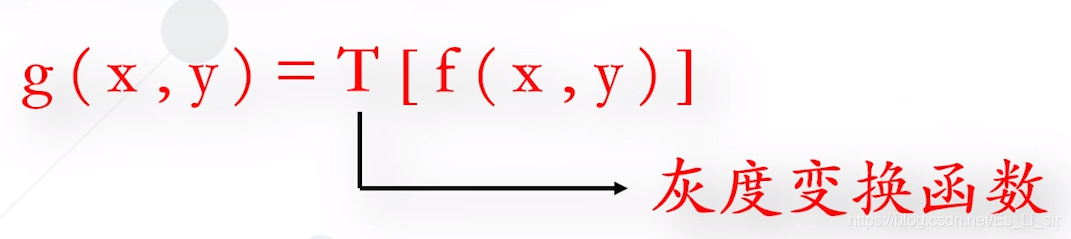
其中T[ ]是对f在(x,y)点值的一种数学运算,即点运算是一种像素的逐点运算,是灰度到灰度的映射过程,故称T [ ] 为灰度变换函数。
若令f(x,y)和g(x,y)在任意点(x,y)的灰度级分别为r和s,则灰度变换函数中简化表示为:s=T[r]
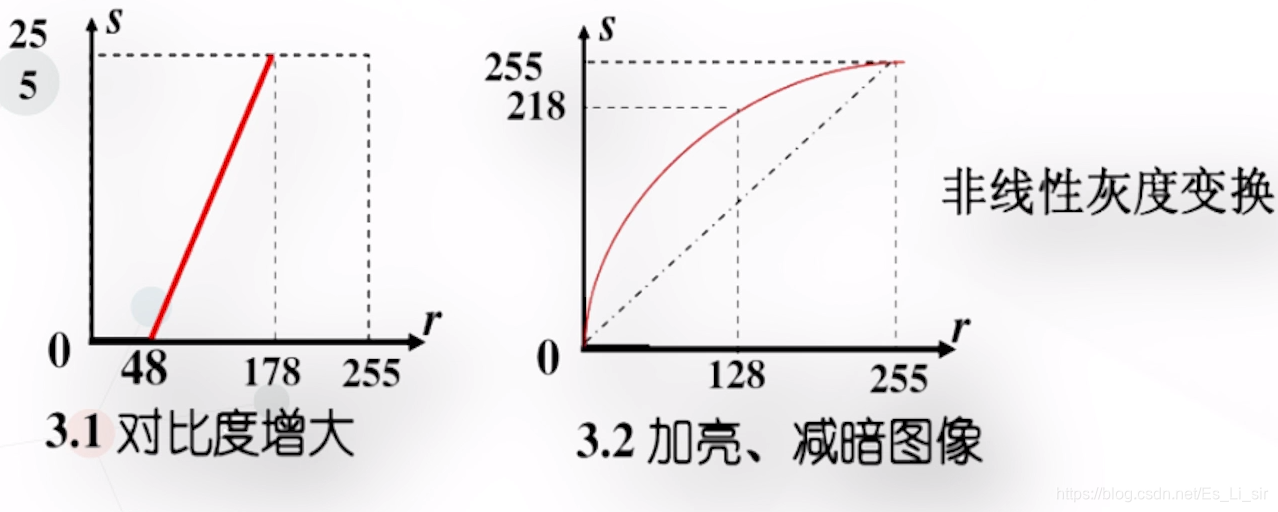
点运算可以改变图像数据所占据的灰度值范围,从而改善图像显示效果。
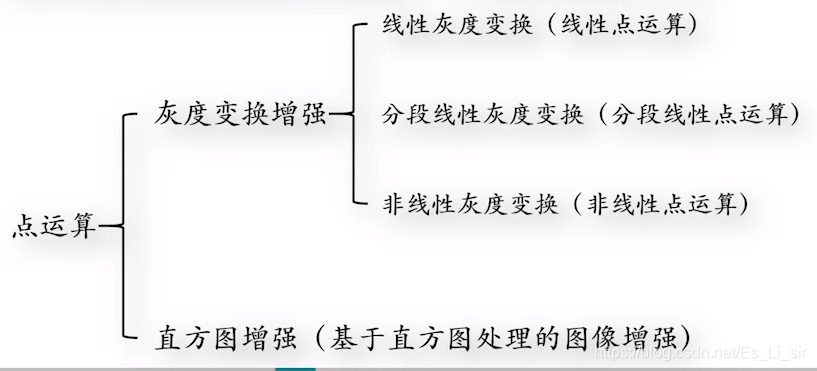
点运算的分类
点运算又称为“对比度增强”、“对比度拉伸”、“灰度变换”等,按灰度变换函数的性质,可将点运算分为:
1.线性点运算
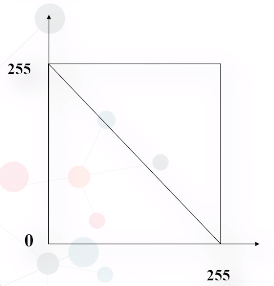
(1)图像求反

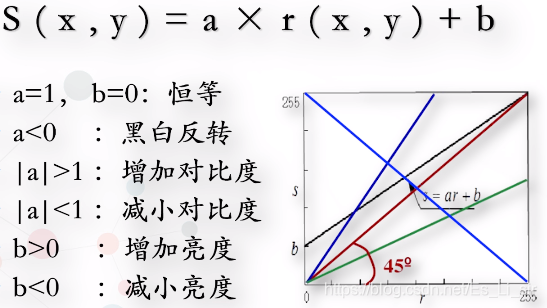
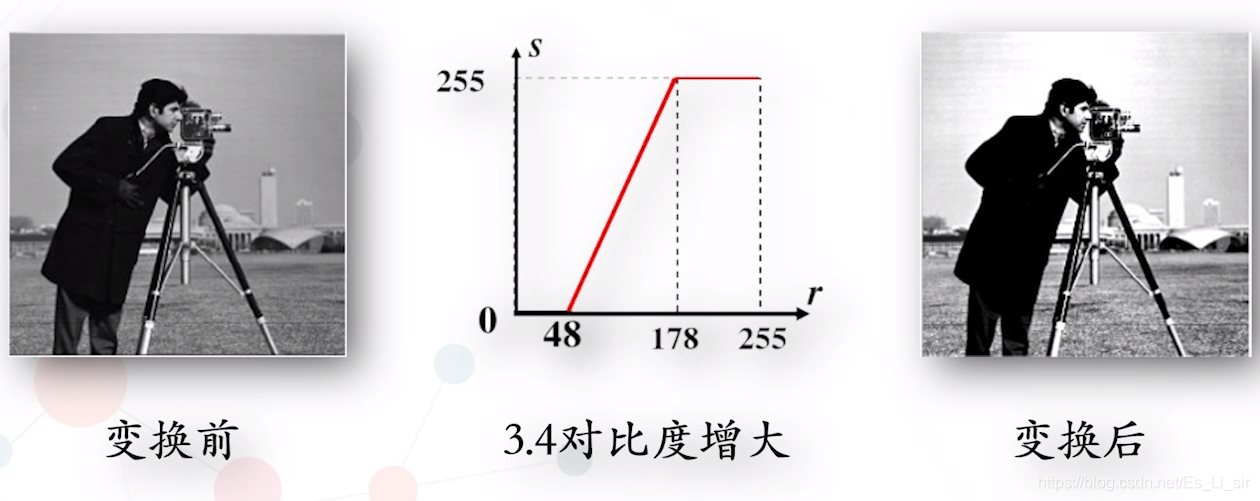
如果a>1,输出图像的对比度增大(灰度扩展)。
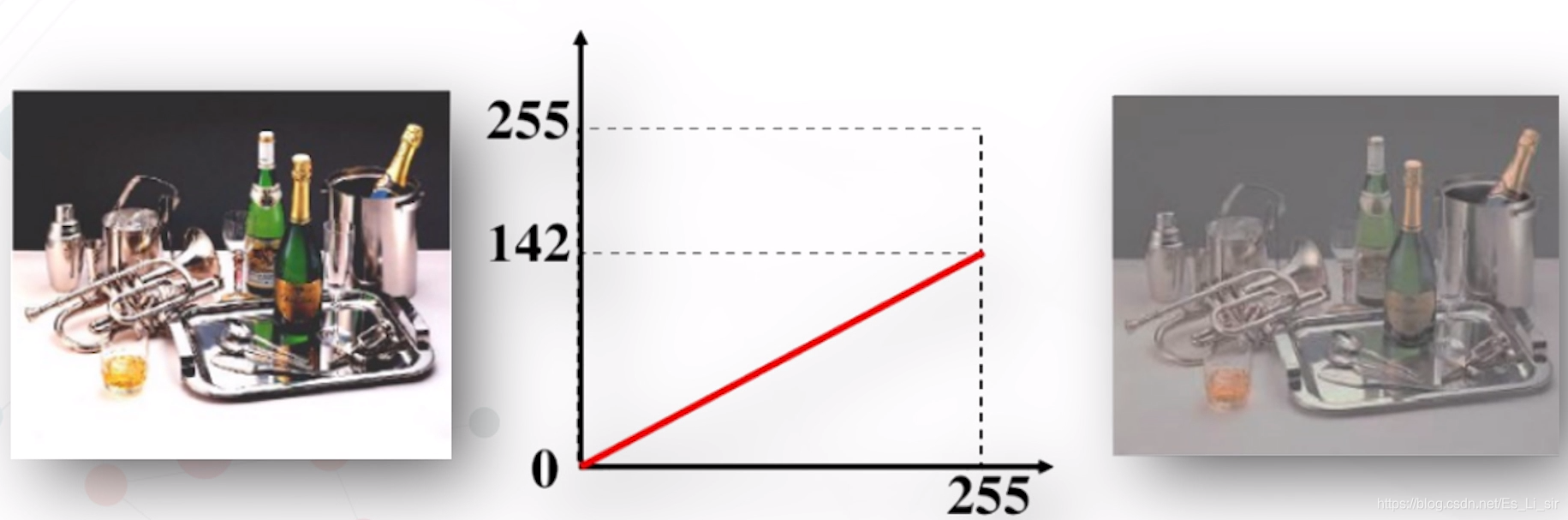
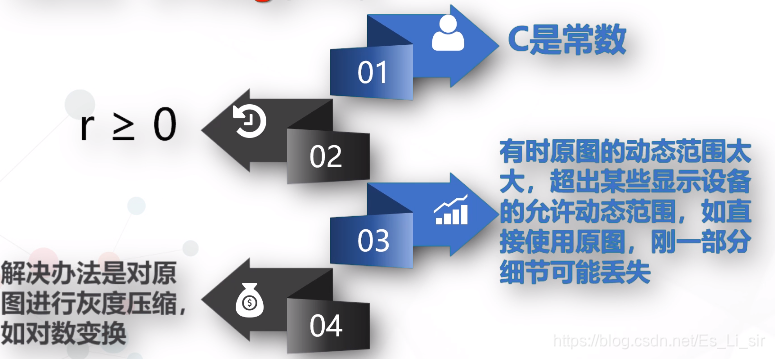
如果0<a<1,输出图像的对比度减少(灰度压缩)
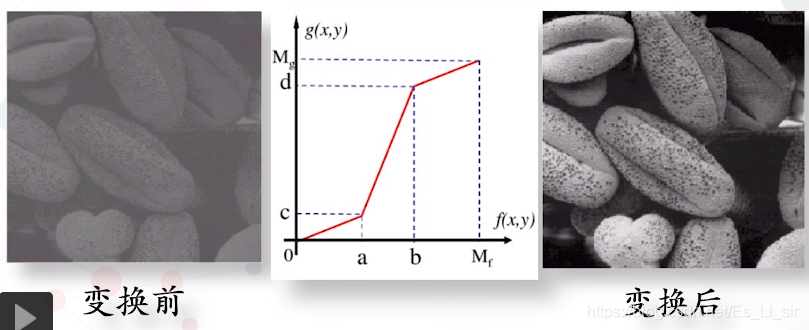
将感兴趣的灰度范围线性扩展,相对找抑制不感兴趣的灰度区域。
设f(x,y)灰度范围为![]() ,g(x,y)灰度范围为
,g(x,y)灰度范围为![]()
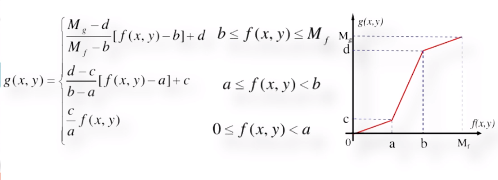
例子:
2.非线性运算
非线性点运算的输出和输入灰度级呈非线性关系,常见的非线性灰度变换为对数变换(对数与反对数)和幂律变换(n次幂和n次根)
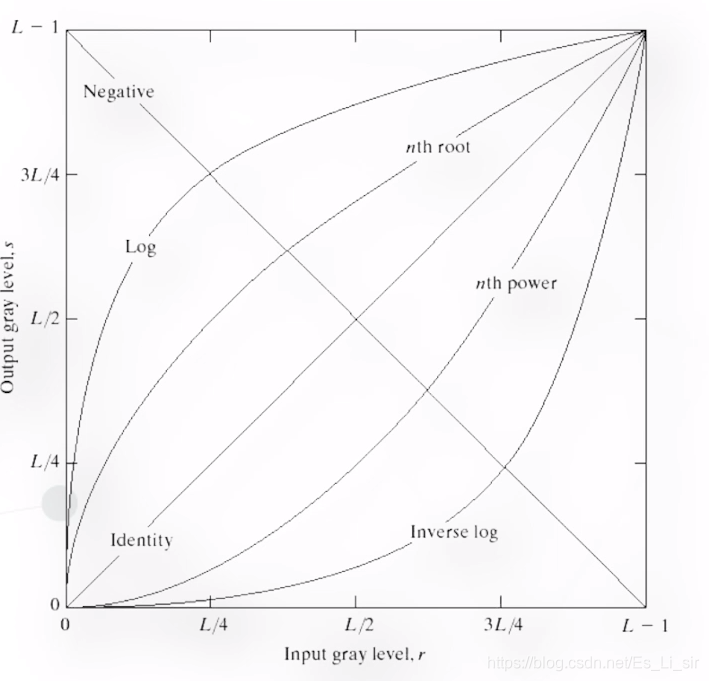
对数变换:S=clog(1+r)



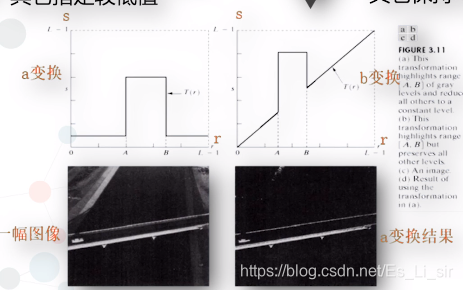
灰度级切片
1.关心范围指定较高值,其他指定较低值
2.关心范围指定较高值,其他保持不变
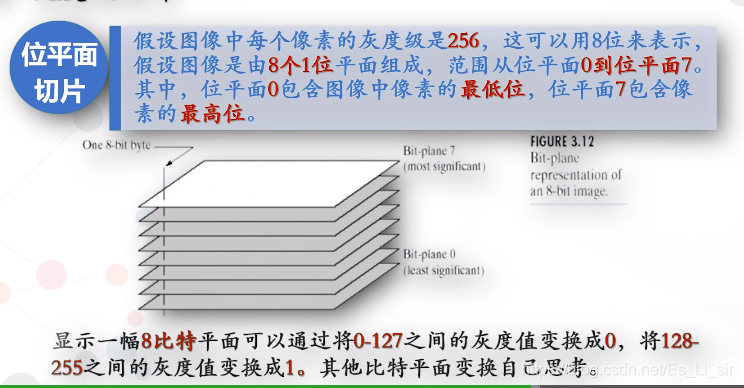
通过对特定位提高亮度,改善图像质量


用四个较高的比特平面就可以还原大致图像,对图像的压缩存储有较好的应用。
代数运算
加法运算的定义
![]()
主要应用举例:去除“叠加性”噪音,生成图像叠加效果








- 获得一个子图像的补图



模板运算:提取感兴趣的子图像



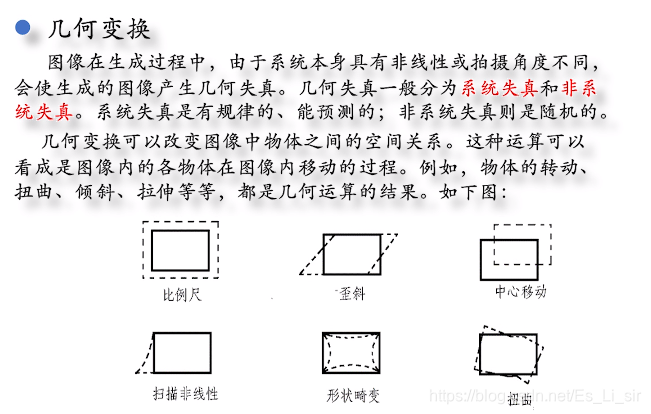

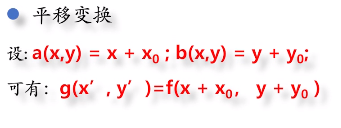

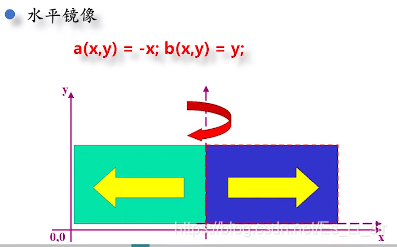
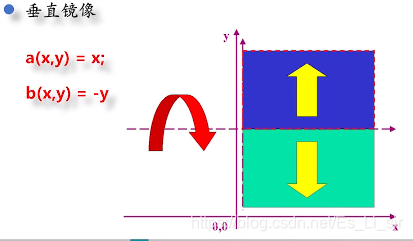
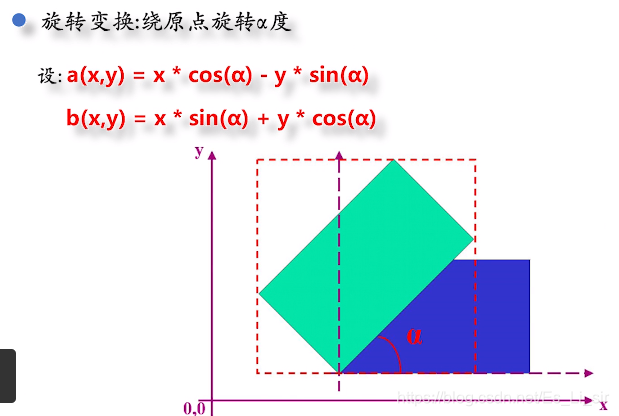

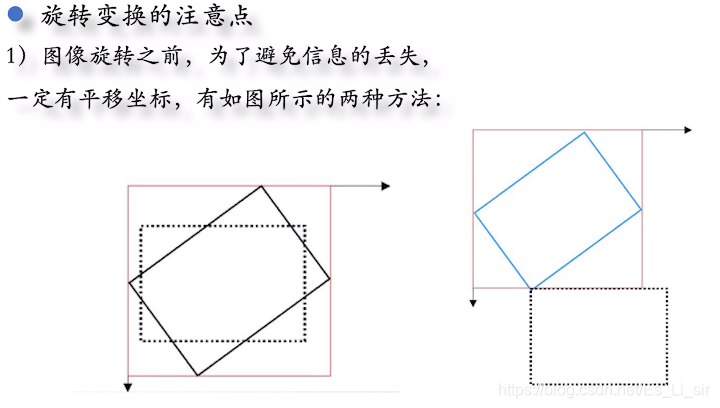


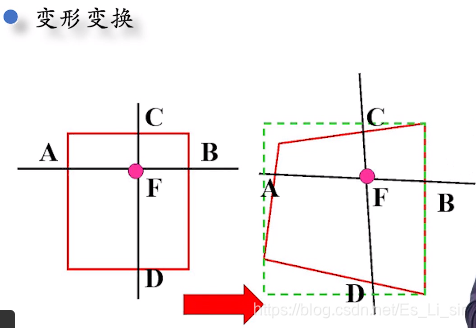

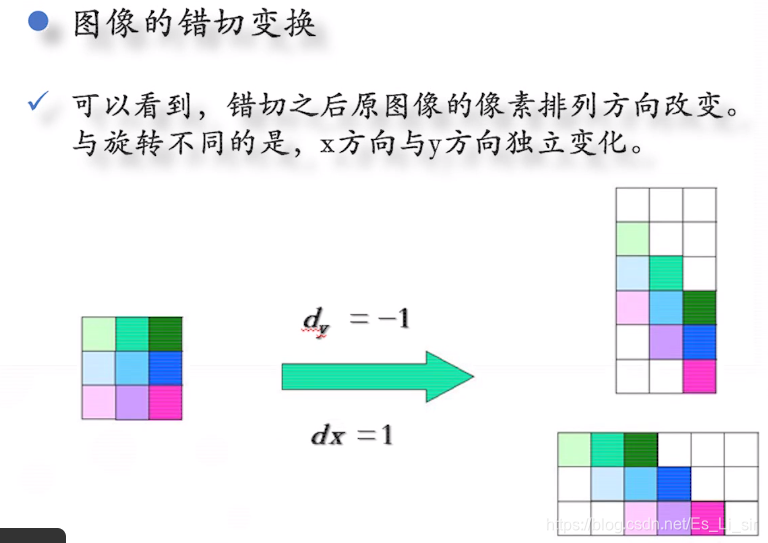
三、直方图变换
定义:一个灰度级范围在[0,L-1]的数字图像,其的直方图是一个离散函数。

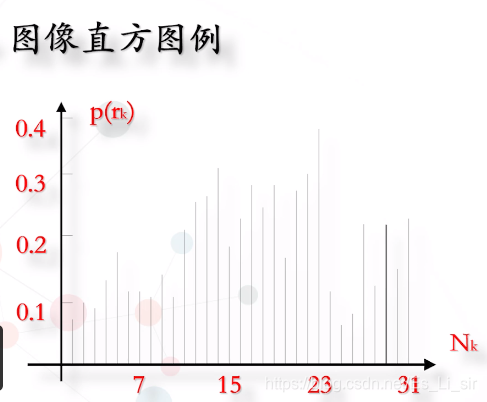
一个灰度级别在范围[0,L-1]的数字图像的直方图是一个离散函数




直方图均衡化




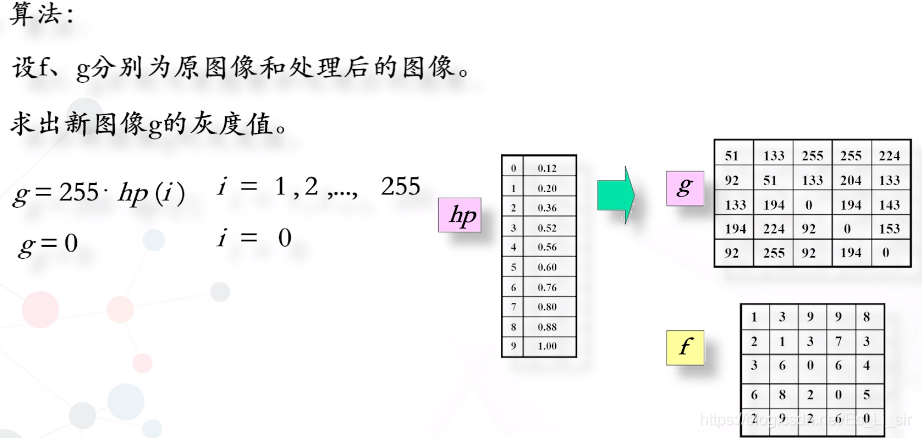

直方图反映了图像的清晰程度,当直方图均匀分布时,图像最清晰。由此,我们可以利用直方图来达到使得图像清晰的目的。