一、图像增强的点运算

图像增强：采用一系列技术，改善图像的视觉效果，或者将图像转换成一种更适合于人或者机器进行分析和处理的形式。

图像增强方法：1.空间域增强：直接对图像各像素进行处理；2.对图像进行傅里叶变换后的频谱成分进行处理，然后逆傅里叶变换得到需要的图像。

目的：
1.改善图像的视觉效果，有利于识别、跟踪和理解图像中的目标。

2.突出图像中感兴趣的信息，抑制不需要的信息，来提高图像的使用价值；

 

一、对比度增强

扩大图像中感兴趣特征的目标；方法：1.灰度变换法，2.直方图调整法

灰度变换是图像增强的重要手段之一，通过调整图像的灰度动态范围或者调整图像的对比度对图像增强。

对比度：明暗的对比程度。可以调整图像的灰度范围对图像进行增强。

1）线性变换：令图像f(i,j)的灰度范围为[a,b],线性变换后图像g(i,j)的范围为[a',b'],这个图是一个线性变换，得到g(i,j)与f(i,j)之间的关系式：

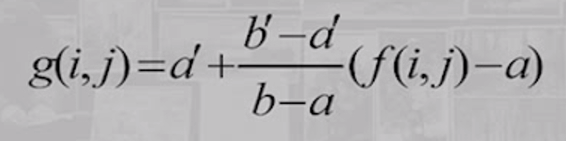
例子：如果图像生成时存在曝光不足或过度的情况，图像灰度可能会局限在一个很小的范围内。在显示器上看到的是一个模糊不清、似乎没有什么灰度层次的图像。

 

对曝光不足的图像用线性变换对图像每一个像素灰度作线性拉伸（由上图）。可看到有效的改善图像视觉效果。

2）分段线性变换

如果只对图像中部分目标感兴趣，这时候需要突出感兴趣目标所在的灰度区间，抑制不感兴趣的灰度区间，分段线性变换可以解决这类问题。

设原图像f(x,y)在[0,],感兴趣目标的灰度范围在[a,b],要把这个灰度范围拉伸到[c,d],可以得到对应的分段线性变换表达式：

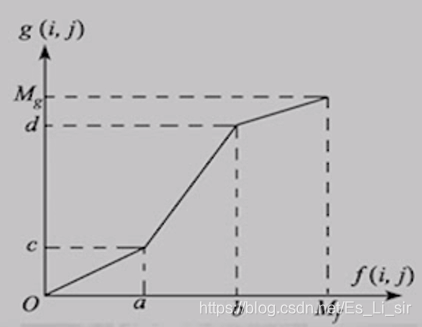
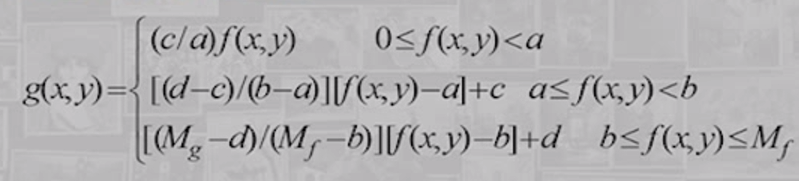
从表达式和图中可以看出，在[0,a)和（b,M]灰度区间内图像是被压缩的。

3）非线性灰度变换

与线性变换不同，非线性变换使用非线性函数作为映射函数，如对数函数，指数函数等，实现对图像灰度的非线性变换。

 

二、对比度增强直方图均衡化

灰度直方图：用来反映数字图像中每一灰度级与这个灰度级出现频率之间的关系，能描述图像的概貌。

直方图修正法包括直方图均衡化及直方图规定化。

直方图均衡化：将原图像通过某种变化，得到一幅灰度直方图均匀分布的新图像。

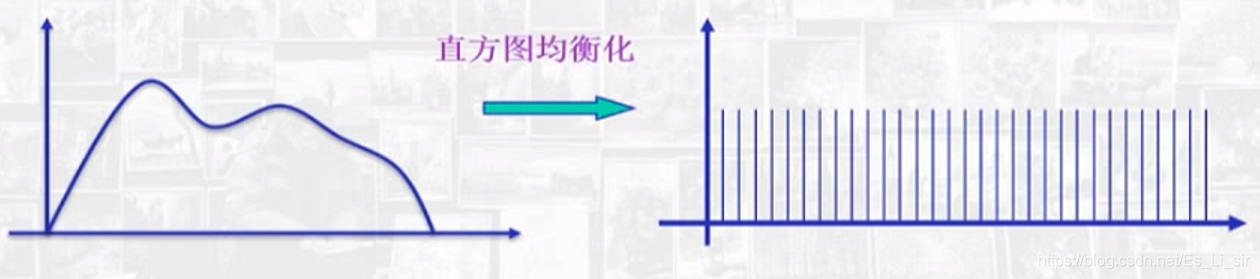
假设用r表示归一化的原图像灰度；用s表示经过直方图修正后的图像灰度。即0<=r,s<=1 在[0,1]区间内的任一个r值，都可产生一个s值，且

s=T(r)

T(r)称为变换函数，满足下列条件：

1.在0<=r<=1内T(r)为单调递增函数； 2.在0<=r<=1内，有0<=T(r)<=1;

条件1保证灰度级从黑到白的次序不变； 条件2确保映射后的像素灰度在允许的范围内。

反变换关系为