二叉树是有限个元素的集合,该集合或者为空、或者有一个称为根节点(root)的元素及两个互不相交的、分别被称为左子树和右子树的二叉树组成。
- 二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
- 二叉树的第i层至多有2^{i-1}个结点
- 深度为k的二叉树至多有2^k-1个结点;
- 对任何一棵二叉树T,如果其终端结点数为N0,度为2的结点数为N2,则N0=N2+1
首先构建二叉树:
1 class Node: 2 def __init__(self,value=None,left=None,right=None): 3 self.value=value 4 self.left=left #左子树 5 self.right=right #右子树
下面给出二叉树的前序遍历/中序遍历/后序遍历
1 def preTraverse(root): 2 ''' 3 前序遍历 4 ''' 5 if root==None: 6 return 7 print(root.value) 8 preTraverse(root.left) 9 preTraverse(root.right) 10 11 def midTraverse(root): 12 ''' 13 中序遍历 14 ''' 15 if root==None: 16 return 17 midTraverse(root.left) 18 print(root.value) 19 midTraverse(root.right) 20 21 def afterTraverse(root): 22 ''' 23 后序遍历 24 ''' 25 if root==None: 26 return 27 afterTraverse(root.left) 28 afterTraverse(root.right) 29 print(root.value)
下面给出一个例子,验证一下程序
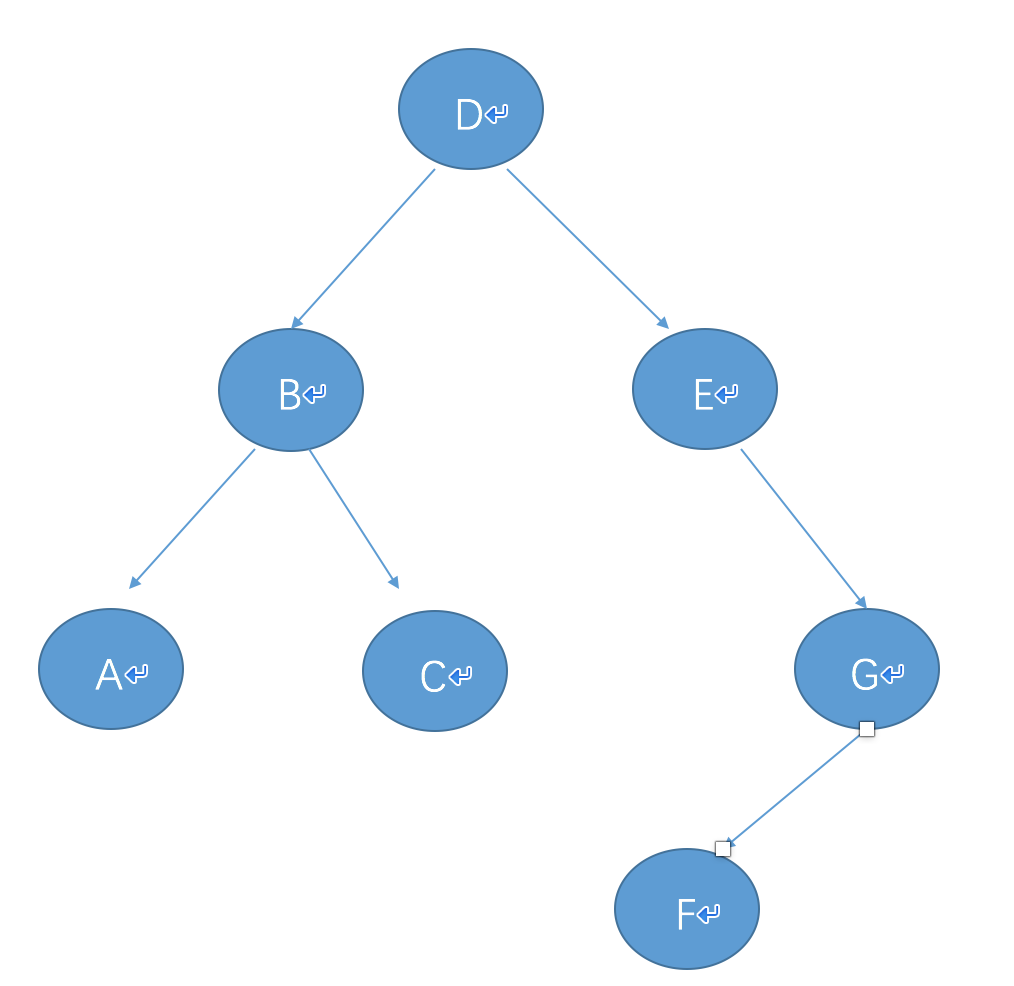
1 if __name__=='__main__': 2 root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F')))) 3 print('前序遍历:') 4 preTraverse(root) 5 print('\n') 6 print('中序遍历:') 7 midTraverse(root) 8 print('\n') 9 print('后序遍历:') 10 afterTraverse(root) 11 print('\n')
输出的结果为
前序遍历:
D
B
A
C
E
G
F中序遍历:
A
B
C
D
E
F
G后序遍历:
A
C
B
F
G
E
D 那么,如果我们已知二叉树的前序遍历和中序遍历,求这棵二叉树的后序遍历
1 preList = list('12473568') 2 midList = list('47215386') 3 afterList = [] 4 5 def findTree(preList, midList, afterList): 6 if len(preList) == 0: 7 return 8 if len(preList) == 1: 9 afterList.append(preList[0]) 10 return 11 root = preList[0] 12 n = midList.index(root) 13 findTree(preList[1:n + 1], midList[:n], afterList) 14 findTree(preList[n + 1:], midList[n + 1:], afterList) 15 afterList.append(root)
结果为:
['7', '4', '2', '5', '8', '6', '3', '1']
1 如果以上面的前序:DBACEGF和中序:ABCDEFG,得到的结果为: 2 ['A', 'C', 'B', 'F', 'G', 'E', 'D']



















,功能和目标)