
来源:集智俱乐部
作者:Guillem Collell、Jordi Fauquet
译者:张澳
审校:刘培源
编辑:邓一雪
导语
信息和能量之间的关系已经在物理学、化学和生物学中得到了广泛的研究。然而,这种联系并没有在神经科学领域形式化。2015年,美国麻省理工学院与西班牙巴塞罗那自治大学的研究者合作发表文章,梳理了信息论与热力学的理论联系,提出了链接物理大脑和认知模型的框架。本文是对论文的全文翻译。
研究领域:自由能,负熵,大脑热力学,认知模型,信息论
目录:
摘要
1. 引言
2. 热力学与大脑活动
3. 信息论与认知
4. 热力学与信息论的关系
5. 讨论
摘要
脑与心智的关系是一个重要的科学和哲学问题,我们还远远没有完全理解。我们工作的一个关键点是注意到热力学提供了一个方便的框架来模拟大脑活动,而认知可以用信息论的术语来模拟。事实上,到目前为止,已经提出了几个与这两种方法相悖的模型。第二个关键点是热力学和信息论之间存在着深刻的理论联系。事实上,一些著名学者声称,热力学定律只不过是信息论中的定律。与物理学或化学不同,神经科学目前缺乏对信息和能量间关系的形式化。本文从信息论与热力学的理论联系出发,提出了一个连接物理大脑和认知模型的框架。最后,本文旨在进一步探讨认知和神经活动之间的形式关系。
1. 引言
大脑是一种用于处理信息的热力学装置。因此,经常以热力学术语 (La Cerra, 2003; Varpula et al., 2013) 建模大脑活动,以信息论术语 (Anderson, 1996; Friston, 2010) 建模认知过程。这两种不同的方法,分别产生了对大脑和认知过程的精确描述。然而,他们的统一将极大地增加我们对大脑活动如何与认知相关的理解,并反过来将促进两种观点 (Colell and Fauquet, 2014) 的发展。至关重要的是,信息论与热力学之间有着深刻的理论联系。这两个学科之间的一些经典联系是兰道尔极限 (Landauer, 1961) 、处理信息的能量成本 (Bennett, 1982) 、吉布斯和玻尔兹曼公式以及熵与负熵的概念 (Schrodinger, 1944; Brillouin,1953)。有趣的是,熵同时是信息论和热力学中的核心概念。尽管在不同理论中它是不同量的度量,但这些量呈现出重要的理论关系,下面将讨论这些关系。事实上,一些作者认为热力学和信息论之间的关系更为密切,并声称热力学定律只不过是信息论中的定律而已 (Rothstein, 1951; Brillouin, 1953)。值得注意的是,上述联系可以作为一套强大的工具以统一基于热力学的大脑模型和基于信息的认知模型 (Colell and Fauquet, 2014)。例如,两个模型的方程是否一致还有待研究。在这个意义上,如果将热力学度量转换为信息度量,那么以能量度量来预测系统在某方向变化的热力学模型,其预测结果应该与基于信息的预测模型一致。
为了简要介绍信息与物理间的关系,让我们回顾1867年提出的思想实验,即麦克斯韦妖悖论。在我们看来,这个悖论不仅有助于理解热力学和信息论之间的关系,而且有助于深入了解思维计算如何与能量和信息相联系。简而言之,考虑一个被分成两部分的容器,a 和 b,两者在相同的温度下装入相同的气体。一个微小的麦克斯韦妖守卫着 a 和 b 之间的活动门,当一个速度比平均值快的分子朝 a 移动时,麦克斯韦妖过快速地打开活动门,在分子通过后立即将门关闭。类似地,麦克斯韦妖允许比平均速度慢的分子进入 b。经过一段时间后,a 中的温度(即平均分子速度)将高于 b 中的温度。这意味着系统的熵 (目前为止是无序的) 会减少,从而明显违反了热力学第二定律定律,即熵在孤立系统中只能增加。之后,这种温差可以用来做功 (Feynman et al.,1998)。直到提出麦克斯韦妖悖论一个多世纪后,人们才完全解决它。后文将给出解决方案及简要评论。值得注意的是,即使以前从未见过信息和熵的任何形式化概念,人们也可以直观地从这个思想实验中认识到,关于系统(冷分子和热分子)的“知识”(译注:知识属于信息)可以以某种方式转化为有用的能量。而与此相反的事实,即能量可以转化为信息,也许从一开始被广泛接受。因为在数字时代,对于任何人来说,电脑消耗能量就是为了编码或删除数据,这并不令人惊奇。
迄今为止,从热力学的观点 (Kirkaldy,1965; La Cerra,2003; Varpula et al., 2013) 以及从信息论框架 (Anderson,1996; Friston and Stephan,2007) 已经提出了几个大脑和认知模型。然而,信息论和热力学之间的联系还没有在神经科学中形式化 (Del Castillo and Vera-Cruz, 2011; Colell and Fauquet, 2014) 。本文旨在进一步阐述我们在前一篇论文 (Collell and Fauquet, 2014) 中介绍的观点,即建立一个合适的框架来连接基于信息的认知模型和基于热力学的大脑模型。在这方面,这项工作的主要贡献是从信息论和热力学间经典联系 (见图1) 的角度来研究这种关系。最终,本文旨在扩展脑活动和认知之间的形式联系。

图1. 通过热力学和信息论之间的经典联系,大脑活动(左)和认知模型(右)之间的联系(中)
本文的结构如下。第一节中,我们将分析如何以热力学框架对大脑活动建模。第二节中,我们提出了Friston基于信息的模型,并列举了从大脑和认知活动中获取信息度量的不同方法。第三节中,我们首先讨论了信息论和热力学之间的经典联系,并分析应该如何将其应用到大脑中。其次,我们应用信息论和热力学之间的经典联系,在先前描述的大脑模型和认知模型间搭建桥梁。随后,我们给出了如何通过该框架解决自发性(适用于大脑和认知活动)问题的建议。最后,我们总结和分析了该方法的贡献,并提出了未来的研究方向。
2. 热力学与大脑活动
开放耗散系统热力学综述
热力学的一个核心概念是熵。它通常被认为是系统的无序程度,但是它的精确定义 (Feynman et al.,1965) 等于以分子振动形式耗散而不能用于产生功的能量。例如,回顾麦克斯韦妖的背景,初始状态和最终状态的能量相同,因为两个状态分子振动的数量相同。但在初始状态下,不可能使用该能量来产生功。物理熵(即 S )的第一个形式化定义是在1856年由克劳修斯(Classius)提出的。状态 a1和 a2之间的熵变化 ΔS 对应于
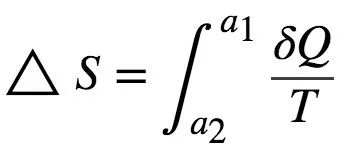
其中 δQ 代表热力学过程增加的热量,T 代表系统的绝对温度。物理熵的国际单位为焦耳/开尔文(J/K) (Feynman et al., 1965)。
如上所述,热力学第二定律表明,除了根据其概率公式的小的随机涨落,任何孤立系统的熵只会增加。更形式化地说,该定理可以表示为 dS/dt ≥0 (Prigogine,1978) 。其中,系统如果不与环境交换物质与能量,则为孤立系统,如果两者都被交换,则为开放系统。值得注意的是,热力学第二定律能够完整刻画自发过程(即无需外界帮助即可发生的过程)。只有当宇宙总体的熵增加时,自发过程才会发生。因此,熵不像能量,能量既不能被创造也不能被破坏(能量守恒定律),熵在一个孤立的系统中只能被创造而不能被破坏(热力学第二定律)。
在这一点上,为了理解生命的热力学,特别是大脑的热力学,一个基本问题自然而然地出现了:生命系统怎么可能倾向于进化到熵值较低的状态,也就是说,更高层次的组织?事实上,这并不是一个真实的矛盾,而只是与热力学第二定律的矛盾。首先,让我们回顾一下,热力学第二定律是为孤立系统而制定的,相比之下,活系统则是典型的开放系统。因此,为了减少生命系统的熵值,必须在其它地方增加熵值,从而使宇宙总体上熵增加。例如,在 DNA 合成过程中有序性增加,但其代价是ATP(三磷酸腺苷分子,在生物中普遍存在的供能分子)的破坏(即增加无序性),熵从总体而言仍是增加的。至关重要的是,生命系统的一个基本定律表明,如果熵达到一定的阈值,有机体的结构和功能将受到威胁 (Schrodinger,1944)。因此,系统内任何显著的熵增必须通过其边界被迅速消除。例如,呼吸作用不仅产生 ATP 分子,而且还会产生一种废物,这种废物必须随后从细胞中排出。
负熵或自由能作为熵的“对立”概念随即产生。它是由薛定谔 (1944) 引入的,能够提供一个适用于研究生命系统的热力学框架。他最初将其称之为负熵,因为在物理意义上,它可以被解释为产生功的可用能量,这与熵的定义恰相反。例如,在神经元出现尖峰(主要是 ATP)前,或者当神经元中存在温度梯度时(像麦克斯韦妖的情况一样)。物理负熵可以用亥姆霍兹自由能公式来描述 (Prigogine,1978):
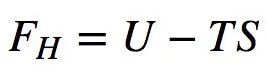 (式1)
(式1)
其中 U 是系统的总内能,T 是其温度。
大脑的热力学模型
一般来说,大脑活动的热力学模型均表现出两个重要特征: (1)大脑被认为是一个通过其边界消除熵的装置,并由自由能(产生于以 ATP 为主的化学物质)提供能量;(2)热力学第二定律被认为是驱动大脑活动的主要原理 (Kirkaldy,1965; La Cerra,2003; Del Castillo and Vera-Cruz,2011; Varpula et al.,2013)。
考虑到生命系统为了维持生命必须满足熵的约束,应用普利高津 (1978) 提出的以下方法是方便的。也就是说,将熵的总变化 dS 分解为内部熵的增加 diS 和穿过系统(如大脑区域或神经元,见图2)边界交换的熵 deS。
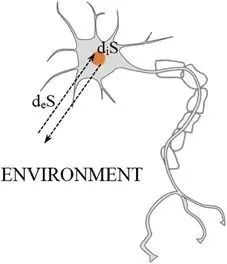
图2.神经元内外的熵交换。改编自普利高津 (1978).
重要的是,由于系统内部必须满足热力学第二定律,所以在每个神经过程之后必须立即得出 diS > 0。然而,这种熵增必须通过神经元的边界被消除。这可以被表示 (Del Castillo and Vera-Cruz, 2011) 为:
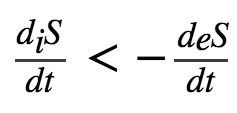
自组织系统的一个基本特性是,当熵的增加超过当前系统结构可以耗散的极限时,可能会涌现新的结构(Prigogine,1978; Stephen et al.,2009),如认知重组。此外,为了恢复产生功(如传递一系列新的神经元刺激)的能力,必须有自由能 (ATP) 流入神经元或大脑区域。这种自由能是通过氧气和葡萄糖的反应来提供的,而氧气和葡萄糖的输送则由血液完成 (Howarth et al.,2010)。下面的等式描述了开放耗散系统(尤其是大脑)的局部熵交换率 (Del Castillo and Vera-Cruz,2011):
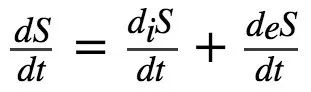 (式2)
(式2)
更详细的描述可将 diS/dt 分解为不同的不可逆过程及其对应的广义力,即:
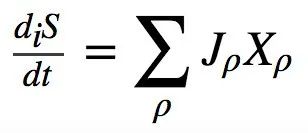 (式3)
(式3)
其中 Jρ 是各种不可逆过程 ρ (化学反应、热流、扩散等) 的速率, Xρ (吸引力、温度梯度、化学势梯度等)为其对应的广义力。
需要注意的是,上述描述对平衡系统和满足局部平衡假设的系统都适用。该假说认为,在给定时刻,可将失去平衡的系统视为处于平衡状态的齐次系统(如果一个系统的性质不依赖于其位置,则该系统被称为齐次系统)。换句话说,局部平衡假设系统分裂为一定数量的胞室,这些胞室足够大,使其可以忽略微观涨落的影响,但同时它又足够小,使得平衡对每个胞室都是很好的近似。因此,在一个给定的是个,每个胞室都达到平衡 (Lebon et al.,2008)。局部平衡假说适用于那些微观时间尺度大大短于宏观时间尺度的过程。例如,两个连续粒子碰撞的间隔所对应的微观时间(比如10-12秒)相比于一个宏观过程(比如持续约1秒)。然而,一些远离平衡的过程不能满足局部平衡假设。当微观时间尺度和宏观时间尺度具有可比性时,就会发生这种情况。例如,在涉及缓慢弛豫时间的过程中,如聚合物溶液或超导体; 或在高频现象中,如超声波在稀释气体中的传播或液体中的中子散射。然而,如果系统与其他更快弛豫的变量耦合,那么仍然可以在远离平衡的情况下定义热力学量(如温度或熵)(Vilar and Rubí,2001),从而能够描述系统。其基本思想是引入其它自由度来增加维数,从而减少弛豫时间。例如,在扩散过程中,Vilar 和 Rubí (2001) 提议将速度作为一个新的变量,尽管并不总是需要这样。总之,为了准确描述任何涉及变量的慢弛豫时间或高频率的神经过程,需要考虑将不可逆热力学的设置拓展。
Varpula 等人 (2013年) 用热力学第二定律作为中心假设模拟了神经元电流活动。该模型指出,在最短的时间内消耗自由能是驱动大脑电活动的主要原理。换句话说,神经网络中的电流会自己寻找在最短时间内消耗更多自由能的通路。从这个意义上讲,神经网络被认为是记忆的寄存器,可以通过激活特定的路径来检索、巩固或重新组织记忆,类似于河流侵蚀自己的景观并影响自己的流量。因此,记忆通过一次又一次地刷新特定的能量流模式而增强,并且在路径未得到加强时而消失。值得注意的是,该模型仅利用热力学第二定律,就能够解释许多大脑过程,如学习、联想或记忆检索。
值得指出的是,几种神经成像技术可以用于测量大脑中的能量活动。一个广泛使用的方法是功能性磁共振成像(fMRI)。该方法测量与血氧水平相关的(blood oxygen level dependent,BOLD)信号,这些代谢变化间接地反映了潜在的神经活动。另一个著名的测量方法是脑电图(EEG)。用这种方法记录的神经电活动是通过测量分布在头皮上的多个电极的电压差来获得的。最后,单细胞记录是测量单个神经元能量活动最准确的方法。该方法将微电极插入大脑,测量单个神经元的动作电位。但是,这是一种侵入性的方法,不能应用于人类研究。因此,最佳的测量方法在很大程度上取决于研究的情境和对象。
3. 信息论与认知
在介绍Friston基于信息的模型之前,我们将简要概述一些重要的定义和信息论的结果。香农的信息论最早是在1948年的通信背景下提出的,该场景包括一个发送端、一个接收端和一个通过信道发送的消息组成(Shannon,1948)。符号 xi 的信息被定义为
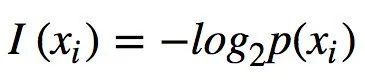
其中 p(xi)对应给定消息中符号 xi 出现的概率。当对数的底数为2时,信息以比特(位)表示。因此,I(xi)等于编码仅由符号 xi 组成的消息所必需的位数。xi 的可能性越小,所需的位数就越多。或者,可以将I(xi)理解为观察 xi 的“惊奇(surprise)”量。
香农熵用 H 表示,其对应于消息中的期望信息或每个符号的不确定性,其中消息为 n 个不同符号 x={xi} ,i ∈{1,... ,n},每个符号出现的概率为 p(xi)。即
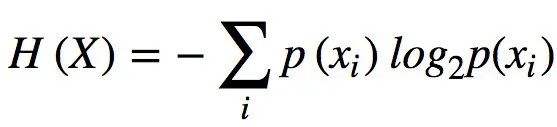 (式4)
(式4)
在无噪声信道的背景下,信息论的一个基本结果就是所谓的香农信源编码定理(Shannon's source coding theorem)。该定理指出,不能将消息压缩到熵的界限以内而不丢失信息。
Friston基于信息的模型
在我们看来,特别值得关注 Friston 基于信息的模型(Friston and Stephan,2007; Friston, 2010)最近的贡献。它提供了对认知过程(如知觉、学习或推理)的广泛描述,并准确地解释了知觉过程 (Moran et al.,2013)。
Friston理论的核心概念叫做自由能(free energy)。在该情况下,自由能 F 被定义为“惊奇”的上界或[ log-evidence-ln p (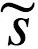 | m)],它与感官输入
| m)],它与感官输入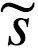 和世界模型m相关的。可以将自由能理解为惊奇加上一个正项,后者为 Kullback-Liebler 散度或交叉熵,即:
和世界模型m相关的。可以将自由能理解为惊奇加上一个正项,后者为 Kullback-Liebler 散度或交叉熵,即:
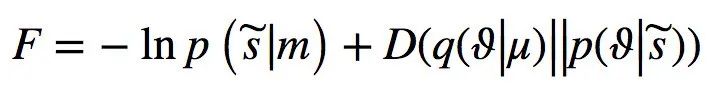 (式5)
(式5)
其中 ϑ 是引起感官状态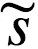 的未知量,μ 代表大脑的内部状态。假定个体将世界的概率表征编码为内部状态 μ。则D (q (ϑ | μ) | p (ϑ |
的未知量,μ 代表大脑的内部状态。假定个体将世界的概率表征编码为内部状态 μ。则D (q (ϑ | μ) | p (ϑ |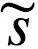 ))项是交叉熵,代表认知密度 q (ϑ | μ)与导致 ϑ 的真实分布 p (ϑ |
))项是交叉熵,代表认知密度 q (ϑ | μ)与导致 ϑ 的真实分布 p (ϑ |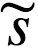 )之间的差异。认知密度(recognition density)对应于主体对输入
)之间的差异。认知密度(recognition density)对应于主体对输入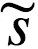 原因的概率表征。从概念上讲,可以将自由能 (公式5) 看作: F = 惊奇 + 交叉熵。(F=Surprise+Cross Entropy)
原因的概率表征。从概念上讲,可以将自由能 (公式5) 看作: F = 惊奇 + 交叉熵。(F=Surprise+Cross Entropy)
Friston理论的核心原理是所谓的自由能最小化。也就是说,为了保存生命,自组织的生物主体应该避免出现令人惊奇的状态。为此,它们的自由能必须最小化。例如,鱼可以通过避免离开水来最小化自由能 (Friston,2010)。至关重要的是,主体可以通过改变其内部表征来使交叉熵项最小化,也就是说,通过改变识别密度来更好地逼近真实分布。通过主动推理(即优化感知),主体通过贝叶斯推断更新其内部表征,使随后的预测错误最小化。在这个意义上,系统隐含地编码了环境的概率模型。至关重要的是,主动推理(即改变期望)和行动(改变结构和避免惊奇状态)是主体最小化其自由能的两种可能机制。
有趣的是,通过方程(5)的代数操作,可以得到以下自由能的重新表述:
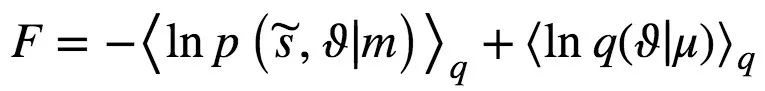 (式6)
(式6)
其中-< lnp (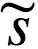 , ϑ|m) > q 项是[在密度 q(ϑ|μ)下]主体寻找由某个 ϑ 引起的感官输入
, ϑ|m) > q 项是[在密度 q(ϑ|μ)下]主体寻找由某个 ϑ 引起的感官输入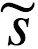 的预期惊奇。Friston和Stephan (2007) 根据该项的物理类比,将其称为期望吉布斯能。第二项对应于变量 ϑ 引起的熵。因此,该公式在概念上等价于以下关系: F = 期望能量-熵,这与物理学中的亥姆霍兹和吉布斯自由能公式有着惊人的相似。
的预期惊奇。Friston和Stephan (2007) 根据该项的物理类比,将其称为期望吉布斯能。第二项对应于变量 ϑ 引起的熵。因此,该公式在概念上等价于以下关系: F = 期望能量-熵,这与物理学中的亥姆霍兹和吉布斯自由能公式有着惊人的相似。
Friston模型借用了统计物理学、生物学、微观经济学或机器学习等不同学科的概念和想法 (Friston,2010)。然而,可以用信息论的术语清晰解释其方程。事实上,自由能是一个来自信息论的概念,用来作为一个模型的证据度量。统计学中的信息极大原理只是自由能最小化原理的一个特例。这种方法采用了同样的自由能概念,但以感官输入为数据,并通过大脑对模型编码。此外,在简化的假设条件下,自由能只能看作是预测误差。
值得注意的是,Friston 的假设已经得到了实证数据的支持。例如,脑电图记录显示,自由能最小化原理能够预测神经元在重复暴露后的神经反应抑制 (Moran et al.,2013) 。此外,值得注意的是,存在其它关于认知的计算模型,例如著名的 ACT-R (Anderson,1996)。然而,Friston模型以信息的视角,对学习过程提供了一个合适的描述,使其更符合本文提出的框架。此外,其方程展示了一个与其对应热力学概念的惊人相似性,与基于物理原则的模型建立了桥梁。
大脑活动与认知的信息度量
在这一点上,人们很自然地会问,从哪里可以获得大脑活动和认知中的信息量,这些信息是刺激本身所固有的,还是在大脑计算中产生的。事实上,不同的信息度量可能适合不同的情况、研究对象或度量的可得性。例如,在主要的认知过程中(如视知觉),刺激的信息内容可能很容易获得。然而,这种方法显然不可能用于研究像问题解决这样的高级认知过程。下面我们介绍了一些已经应用的方法,以及一些新的想法。
方法1
信息测量可以直接从刺激特征中获得。这种方法尤其适用于感知任务,因为这些任务的相关刺激特征很容易获取。值得注意的是,Laughlin 等人 (1998) 第一次应用这种方法获得了苍蝇视觉感官系统处理一比特信息所需的能量成本。特别是,已知数量的信息以光强波动的形式传递到苍蝇视网膜的感光器。有关这种方法的更详细描述,请参阅 Borst 和 Theunissen (1999) 的评论。
方法2
信息度量可以直接从任务的复杂性中估计出来。对于一个特定的认知任务,系统可能状态(中间步骤、反应、响应等等)的数量通常是有限的,每种状态都有一定的发生概率。该方法的基本思想是计算一个任务的香农熵 H =-∑pilog2(pi)。直观地说,记忆 ABBA 序列[ I = log2(24) = 4位]与记忆ABBBAABAABABAB序列[ I = log2(214) = 14位]的成本并不相同。这种方法类似于用吉布斯公式估计物理熵(见第三节)。计算过程中,可能有多个中间步骤的组合 (微观态) 导致相同的结果或行为响应(宏观状态)。特别是,任务总体的熵或信息负荷与所有可能的微观态的信息含量的加权平均数相对应。另一个简单的假设案例见图3。
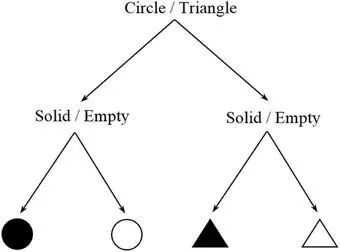
图3. 两个选择任务的决策树。
图3中有两个不同的选择,一个关于形状,另一个关于颜色。假设这四个结果可能性相等,那么这个任务的信息估计将是 log2(22) = 2位,或者相当于回答两个是/否问题。当然,这个简化的描述只是为了给这个方法一个直观的概念,并没有试图描述任何在真实的感知情况下会严重影响其信息内容的颜色或形状的细微差别。需要指出,这是一种非常灵活的方法,在确定合理描述任务的方案前,需要进行详尽的检查。例如,Stephen 等人 (2009) 在一个实验中采用了类似的方法,参与者必须从一个相互连接的齿轮系统中预测最后一个齿轮的旋转方向。然而,在这种情况下,随机噪声(即不可预测性)被引入任务,并被参与者视为信息内容的度量。
方法3
神经成像技术,如单细胞记录、功能磁共振成像和脑电图,可以提供能量消耗的度量。同样,也可以用它来推断大脑计算的信息内容,也就是说,直接从神经编码对信息进行估计。在这种情况下,信息内容是从数据的“复杂性”推断出来的。单细胞记录已经被广泛用于动物实验(Borst and Theunissen, 1999) ,但最近有人提出,非侵入性的方法(如功能磁共振成像或脑电图)也可以是一个合适的选择(Assecondi et al.,2015)。该方法中,有许多不同的特征可用于从原始数据估计熵。这些特征包括反应时间,一个脑电波成分的振幅或时延,行为测量,一个或多个体元(voxel)中与血氧水平相关的响应的参数等(Assecondi et al.,2015)。
方法4
机器学习中的一些算法,如人工神经网络(ANN),可对人的学习过程建模。这些技术的优点是学习的信息成本低,且模型参数易得。有趣的是,人工神经网络不仅能很好地从数据中学习,而且还能展示多个互联神经元处理信息的实际神经生物学结构。然而,不能以此推断出算法的其余部分是否复制了实际的底层生物学。事实上,该模型通常通过(随机)梯度下降法拟合,而不打算模拟任何生物过程。尽管如此,如果任务难度发生变化,人工神经网络和实际大脑计算成本之间存在相互关系也是合理的。感知器的现代版本(Rosenblatt, 1958),比如反向传播算法(Hecht-Nielsen,1989)或者 Neocognitron(一种多层次的人工神经网络) (Fukushima,1980),可能是估计简单的学习或感知任务信息成本的合适选择。有趣的是,Brunel 等人 (2004) 已经成功地测试了一种类似的方法,他们使用感知器模型的突触权重来估计小脑浦肯野细胞(Purkinje cell)处理的信息量。因此,人们认为突触功效的改变是记忆和学习的基础,他们的发现揭示了每个浦肯野细胞存储多达5 kb 的信息。另一个有趣的方法是 EDLUT,一种便于对实验设置(如机械臂的执行)建模的模拟软件,该软件基于生物上可行的神经模型(Ros et al.,2006)。最后,我们认为使用 Friston 的学习算法是合适的,它在很大程度上结合了机器学习方法,并且已经被证明能够精确拟合神经数据(Moran et al.,2013)。此外,该模型还具有已经用信息论术语定义的优点。
前三种方法的关键点是必须特别注意相关特征(任务、刺激或数据)的选择和它们将包含在熵计算中的级数(Borst and Theunissen,1999)。信息估计的可靠性在很大程度上取决于这一选择。换句话说,我们“字母表”的符号数目的定义将对最终的香农熵产生相当大的影响。在这方面,选择一些提供信息的特征通常会比考虑太多没有明确假设的特征得到更准确的估计(Assecondi et al.,2015)。
4. 热力学与信息论的关系
能量与信息的经典关系
如上所述,麦克斯韦首先指出了交换信息和物理熵的可能性,从那时起许多作者进一步研究了这种关系 (Feynman et al.,1998)。下面,我们介绍了热力学和信息论之间的一些经典的理论联系。
吉布斯和玻尔兹曼公式
玻尔兹曼 (1877) 从统计力学的角度提出了熵的第一个定义。波尔兹曼公式假设存在 W 个等概率微观态,且系统处于热力学平衡。在这种情况下,系统的熵 S 为
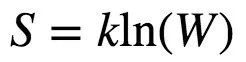 (式7)
(式7)
其中 k 是波兹曼常数,大约为1.38 × 10-23J/K。物理学中微观态的数量是指系统中粒子能够呈现的所有能量状态组合的数量。一般来说,这个数字会随着温度的升高而增加 (Feynman et al.,1965)。通常,会有大量的微观态导致相同的宏观状态,即相同的能量(E)、体积(E)、压力(P)和温度(T)。值得注意的是,玻尔兹曼公式描述了微观条件下的熵(微观态)和宏观条件下的克劳修斯公式(热交换)。此外,玻尔兹曼公式很好地说明了热力学第三定律,即熵在0 K 的温度下恰好为零。在这种情况下,完全没有分子振动,只能导致一种可能的微观态。
更一般地,吉布斯指出,一个系统的熵可以计算如下 (Feynman et al.,1998) :
 (式8)
(式8)
其中 pi 对应于从平衡系综中得到微观态 i 的概率。我们立刻注意到两件事。首先,吉布斯公式与香农熵具有相同的形式,除了波兹曼常数 k 带来的单位变化; 其次,在所有的微观态都是等概率的情况下,进一步假设热力学平衡,吉布斯方程将简化为玻尔兹曼公式。直观地看,假设系统的宏观状态是已知的,根据吉布斯公式,可以把物理熵看作是为了完全确定系统的微观态而需要回答的是/否问题的数量。重要的是,吉布斯公式提供了一个信息视角下的热力学第二定律: 我们关于一个孤立的系统的信息永远不会增加,因为自发过程总是导致信息的丢失 (Rothstein,1951)。因此,根据吉布斯的说法,熵的增加等于我们对系统的信息的减少。
负熵 (布里渊负熵)
如上所述,物理自由能用亥姆霍兹(Helmholtz)公式(方程1)描述。至关重要的是,布里渊(Brillouin)(1953) 创造了“负熵”这个术语,并将这个概念与信息联系起来。他把信息熵和物理熵统一于同一个方程。下面,我们用布里渊 (1953) 论文的简短推理来推导这个公式。首先,我们考虑一个具有P0个等概率状态的系统。如果我们获得关于这个系统的信息 I,并且像麦克斯韦妖对气体所做的那样利用信息,系统可能的状态数量减少到 P1。把两数量比值的自然对数作为信息的度量,这就得到了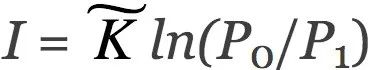 ,其中
,其中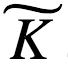 是一个常数。例如,通过选择
是一个常数。例如,通过选择 = log2(e) ,我们可以用比特来度量信息 I = log2(P0/P1)。通过选择
= log2(e) ,我们可以用比特来度量信息 I = log2(P0/P1)。通过选择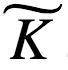 = k (即波兹曼常数) ,应用 Boltzmann 公式[ s = kln (p)]并重新排列项,得到以下关系式:
= k (即波兹曼常数) ,应用 Boltzmann 公式[ s = kln (p)]并重新排列项,得到以下关系式:
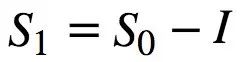 (式9)
(式9)
其中 I 对应于负熵。布里渊提出的信息和物理熵可互换的观点已被广泛接受 (Prigogine,1978; Plenio and Vitelli,2001; Maruyama et al. ,2009)。值得注意的是,利用布里渊方程,对于每个孤立系统,可以通过引入一个信息项(S0-I)≥0来推广热力学第二定律 (Brilouin,1953)。此外,后一种说法带来了一个更深刻的结果,即香农信源编码定理和热力学第二定律之间存在着内在的联系,违反其中一个,则另一个也不成立。
信息处理
Szilard (1929) 证明了从一个系统中获取信息的行为产生熵,或者说,该过程本质上需要能量成本。他指出,确定一比特信息所需的最小能量是 kTln (2) J (或者等价的 kln (2)J/K 熵增)。后来,Landauer (1961) 在计算中研究了同样的现象,发现擦除一比特信息(例如在磁盘中)会产生同样数量的最小热量。一个有趣的事实是,热量的产生是限制现代计算机处理速度的主要原因,而且,事实上,计算机还远远没有达到兰道尔极限。至关重要的是,确定每比特所需的 kTln (2) J 的最小能量成本可以推广到任何其他“操纵”或处理信息的方式,如测量、编码、显示、是/否决定等。
有趣的是,该原理为麦克斯韦妖悖论提供了一个解决方案,即麦克斯韦妖不能以零成本执行所有的计算和测量。因此,麦克斯韦妖必须为测量 (Szilard,1929)、擦除 (Landauer,1961) 或编码 (Bennett,1982) 记忆中的信息付出成本。或者,可以将麦克斯韦妖简单地解释为一种将负熵转化为信息的装置,反之亦然 (Brillouin,1953)。从神经科学的角度,可以从麦克斯韦妖悖论中得出神经计算的下限。事实上,这意味着麦克斯韦妖如何在大脑中进行计算并不重要,但是计算每比特或者每个二进制决策(冷分子和热分子)的能量成本最低,为 kTln (2) J。兰道尔极限在大脑中的合理性将在下一节讨论。
大脑中的能量和信息之间的联系
关键是要注意到,大脑并不是熵约束的例外,因为它必须服从热力学定律。例如,De Castro (2013) 解析性地发现了兰道尔极限为大脑计算的热力学下限。然而,即使进化被认为是“选择”了能量最有效的过程,大脑真实的计算成本并未达到物理下限。首先,因为物理学中考虑的最小处理单元是原子/分子,其运作方式与大脑神经元相距甚远; 其次,神经网络包含了显著的冗余和噪声因素,大大降低其效率 (Narayanan et al.,2005)。
Laughlin et al. (1998) 首次给出了处理感官信息所需的明确能量成本。他们在苍蝇身上的发现表明,对于视觉感官数据来说,一比特信息的能量成本大约是5×10-14焦耳,相当于104个 ATP 分子。因此,神经处理的效率仍然远远低于兰道尔的极限 kTln(2)J。但是一个奇怪的事实是,它仍然比现代计算机高效得多。我们想强调的是,这一能量成本对应于苍蝇的视觉感官处理,因此会因大脑区域、神经元类型或认知过程的不同而有很大差异 (Howarth et al.,2010)。此外,神经噪声和冗余与地形和种群大小有关。一般来说,能量成本随着神经集群的大小而增加 (Narayanan et al.,2005年)。
也许一个更具挑战性的目标是,根据来自内部表征而不是来自外部(如对感官信息的处理)的数据来估计神经信息 (Colell and Fauquet,2014)。深思熟虑、解决问题或创造性思维就是这类任务的实例。我们认为,从“能源-信息交换”的框架来处理这些情况特别方便,因为在这种情况下,只能间接推断信息内容。例如,通过使用前面章节中提出的一些方法,如机器学习、模拟软件或香农熵估计。相反,在任务执行过程中可以首先采取能量度量(如脑电图或功能性磁共振成像),然后利用这些度量推断其信息含量。为了实现从能量到信息的转换,必须考虑到以前关于相关脑区冗余和噪音因素的知识 (Collell and Fauquet,2014)。可以将这些推断的信息度量与独立从执行相同任务的机器学习或模拟软件中获得的估计信息进行对比。我们建议,初始测试应该在简单的感知任务中进行,以便逐渐将该方法应用到日益复杂的认知任务中,并且避免估计信息与实证度量相关的初步结果。从这个意义上说,比起高阶认知任务,知觉更少受启发式的影响。例如,有许多不同的方法来执行心算,其计算成本差异巨大。值得注意的是,最近的研究为之前的假设提供了有希望的实证。Anderson 和 Fincham (2014年) 表明,多体元模式识别可以用来发现任务执行过程中的精神状态。他们能够识别解决数学问题的不同阶段(编码、规划、解决和响应),并通过考虑任务的难度和新颖性来预测每个阶段的处理时间。
大脑皮层网络表现出不同的活动模式,如振荡、同步和神经雪崩(neural avalanches)(Beggs and Plenz,2003) 。其中神经雪崩与本工作相关,因为它与一个被广泛研究的物理学概念——临界性——相关。临界性存在于一些由局部相互作用的非线性单元组成的物理系统中。诸如地震、森林火灾、沙堆、核连锁反应、神经激活等系统都存在临界性。在这些系统中,从某些参数值超过临界值 (阈值) 的单元开始,将相同的变化传递到相邻的单元。因此,级联通过系统中的大量单元进行传播。系统临界点附近的时空分布由幂律描述,具有标度不变性。也就是说,可以在不同的尺度上观察到同样的动力学。至关重要的是,实证证据倾向于证实,大脑皮层活动表现出类似的临界行为,神经雪崩的规模分布遵循幂律(Beggs and Plenz,2003; Haimovici et al. ,2013)。此外,大脑在大部分时间里几乎处于临界状态。在这种情况下,临界参数对应于所谓的分支(branching)参数,该参数被定义为来自同一个祖先的后代的平均数量。也就是说,当一个神经元在当前时间区处于激活状态时,下一个时间区该神经元激活的神经元的平均数量。在分支参数等于1的临界值处,神经雪崩反复发生,信息传输能力最大化。相比之下,亚临界网络产生衰减信号,超临界网络产生类似癫痫的激活(Beggs and Plenz,2003; Haimovici et al. ,2013)。值得注意的是,在神经雪崩和大脑自由能动力学之间建立联系的可能性被建模为寻求在最短时间内消耗自由能(Varpula et al.,2013)。事实上,两个模型都描述了某些神经集群的激活,因此两个框架必须表现出一致性。此外,临界也是从认知角度研究的对象,在该例中用信息论术语对其研究。在这方面,临界值不是指任何热力学量,而是指来自输入的香农熵。Stephen等人 (2009) 提供了一个初步证实的假设,新的认知结构的涌现遵循临界性的普遍原则。他们发现,在熵达到一定的阈值之后,对象对任务的理解经历了一个不连续的变化,从而很快洞察到任务的功能。本质上,仍然有待从不同的角度研究临界值:热力学(Varpula et al.,2013) ,神经分支 (Beggs and Plenz,2003) 和认知信息论 (Stephen et al.,2009) 是相互联系的。此外,临界性在大脑和认知动力学中的存在对信息的处理和传递具有影响,因此,当模型存在引起系统不连续变化的变量时,必须特别注意。然而,如上所述,实证证明似乎证实了大脑在大多数时间处于临界状态附近,在那里信息传输最大化。
连接大脑和认知模型
至关重要的是,基于热力学的模型和基于信息的模型共享一些功能假设: (i)大脑必须避免相变 (即其结构和功能的剧烈变化) 以及大量熵增加ーー如果出现大量熵增加,必须将其迅速消除;(ii)大脑总是在最短的时间内使自由能 (物理或信息) 最小化;(iii)大脑对内部状态、感官输入、行为响应和这些行为结果的适应值之间的概率关系进行编码(Kirkaldy,1965; La Cerra,2003; Friston,2010; Del Castillo and Vera-Cruz,2011; Varpula et al.,2013; Colell and Fauquet,2014)。
上述考虑表明,当处于给定情况时,两种模型将在同一方向上激发系统的行为。换句话说,大脑中的物理自由能的变化方式与Friston信息自由能的变化方式相似。例如,让我们假设主体正面临一个新的情况,比如一个新的环境。由于情况的新颖性,Friston 的惊奇项 ln p (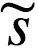 | m)将会很大,导致自由能增加。同样,大脑中也会由于血流量增加而消耗大量的物理自由能(ATP)。随着在最短时间内能够消耗更多能量的神经通路的激活,这些自由能迅速减少,因此 ΔFH< 0。与此类似,随着系统采取行动或在大脑中编码新信息而避免惊奇状态,Friston自由能也会迅速降低。自由能最小值 ΔF < 0 也由此达成。此外,两模式还完成了编码的任务。也就是说,在Friston模型中,系统通过准确更新输入的成因,减少了预测误差。类似地,在热力学模型中,新激活的神经通路将在未来将更容易检索。
| m)将会很大,导致自由能增加。同样,大脑中也会由于血流量增加而消耗大量的物理自由能(ATP)。随着在最短时间内能够消耗更多能量的神经通路的激活,这些自由能迅速减少,因此 ΔFH< 0。与此类似,随着系统采取行动或在大脑中编码新信息而避免惊奇状态,Friston自由能也会迅速降低。自由能最小值 ΔF < 0 也由此达成。此外,两模式还完成了编码的任务。也就是说,在Friston模型中,系统通过准确更新输入的成因,减少了预测误差。类似地,在热力学模型中,新激活的神经通路将在未来将更容易检索。
从社会心理学的角度来看,适应行为可以被理解为个体减少其物理熵和Friston熵的一种机制。例如,法律建立了社会约束和公共教育,最终目的是保证个体的熵不会增加到一个危险的阈值。例如,一个没有受过教育的人可能会面临一些危险情况,而受过教育的人则会避免这些情况。从这个意义上说,对于没有受过教育的个体来说,其Friston熵会更高,因为他大多数时间处于大量的可能状态。换句话说,他将更频繁地处于惊奇的环境中,而Friston熵可以视为令人惊奇的平均值,因此他的Friston熵将增加。
Friston自由能 F 和布里渊的自由能 I 有区别和相似之处。首先,这两个术语都以概率分布的负对数来定义系统的信息量。从这个意义上说,Friston自由能对应于“统计上的惊奇”—— −lnp(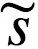 |m) (还需加上一个正项) ,也就是说,大脑接收刺激的不可能性 (即信息量) 有多大。因此,对频繁发生事件的编码仅需较少的比特,比如对于个体而言,它几乎没有新的信息。相比之下,为减少未来遇到的惊奇事件,在神经网络中对极不可能发生的事件进行编码需要更多比特。类似地,布里渊的负熵项 I 也指的是,如果系统获得/处理了更多关于环境或自身的信息,那么信息量将会增加。此外,布里渊的自由能不仅是信息的度量,更重要的是,它与物理意义上的实际自由能相对应。因此,布里渊公式 S1 = S0-I 提供了一个度量 (下限) ,通过处理 I 位信息 (例如,通过合并环境中的 I 位比特) ,大脑内的物理熵S1 - S0可以减少多少。因此,该分析表明,布里渊自由能和Friston自由能在神经处理的背景下具有类似的意义。然而,很明显,Friston公式为布里渊自由能的“浓缩”,特别是应用于自组织生物系统(尤其是大脑)并包括内部状态 μ 等特定参数时。然而,不同于同为能量和信息量的布里渊自由能,没有任何已知热力学单位 (例如,J 或 J/K) 能够明确解释Friston自由能,它只是显示了与亥姆霍兹方程 (公式1) 的相似之处。在我们看来,进一步研究Friston信息测度(如自由能和熵)的热力学含义和等效性是一个有趣的问题。
|m) (还需加上一个正项) ,也就是说,大脑接收刺激的不可能性 (即信息量) 有多大。因此,对频繁发生事件的编码仅需较少的比特,比如对于个体而言,它几乎没有新的信息。相比之下,为减少未来遇到的惊奇事件,在神经网络中对极不可能发生的事件进行编码需要更多比特。类似地,布里渊的负熵项 I 也指的是,如果系统获得/处理了更多关于环境或自身的信息,那么信息量将会增加。此外,布里渊的自由能不仅是信息的度量,更重要的是,它与物理意义上的实际自由能相对应。因此,布里渊公式 S1 = S0-I 提供了一个度量 (下限) ,通过处理 I 位信息 (例如,通过合并环境中的 I 位比特) ,大脑内的物理熵S1 - S0可以减少多少。因此,该分析表明,布里渊自由能和Friston自由能在神经处理的背景下具有类似的意义。然而,很明显,Friston公式为布里渊自由能的“浓缩”,特别是应用于自组织生物系统(尤其是大脑)并包括内部状态 μ 等特定参数时。然而,不同于同为能量和信息量的布里渊自由能,没有任何已知热力学单位 (例如,J 或 J/K) 能够明确解释Friston自由能,它只是显示了与亥姆霍兹方程 (公式1) 的相似之处。在我们看来,进一步研究Friston信息测度(如自由能和熵)的热力学含义和等效性是一个有趣的问题。
神经认知活动中的自发性
在先前的工作中,我们认为自发性可以成为神经科学中一个有趣的研究课题 (Collell and Fauquet,2014)。也就是说已知系统的某些变量,在不借助外界帮助的条件下,要找到条件来确定什么样的神经过程将自然发生。自发的神经活动已经成为神经科学研究的对象,主要目的是为神经雪崩寻找实证证明。然而,据我们所知,到目前为止还没有关于信息或热力学度量的参考文献。自发过程在物理学中已经被热力学第二定律物理实验室很好地描述了。此外,布里渊 (1953) 推广了这一原则,并允许在信息术语中定义物理自发性。同样,化学中的自发过程也有其热力学第二定律,即所谓的吉布斯自由能公式 ΔG = ΔH-TΔS,其中 H 是焓 (即内能加上一个正项)。在这方面,只有当一个过程导致吉布斯自由能 ΔG ≤0时,自发性才是可能的。关键是,这些计算在实际情况下是可行的,因此可以应用于实际预测。然而,神经科学并没有一个可操作的描述自发过程的可计算方程式。在这个方向上,Varpula 等人 (2013) 最短时间内自由能消耗的原理为神经层面上的自发性的提供了理论基础。然而,为了预测认知或神经过程的发生而使用这种自由能度量是不可行的。事实上,需要从不同的神经网络实时记录自由能,以验证电信号确实流入预测的路径。重要的是,Beggs 和 Plenz (2003) 描述了自发神经激活,该过程在分支参数处于临界值(比如公式1)时发生。该描述大量采用文献中的实证支撑,有效地刻画了自发性。尽管如此,它的初始形式需要网络中的每个神经元的单细胞记录。在信息论术语中,Friston模型隐含地将自发过程描述为那些导致信息自由能 F 减少的过程。然而,在实践中,计算方程(5)或(6)中的所有量仍然是不可行的,因为其中某些量(如隐藏的心理状态或原因)对我们和行为主体来说都是不可达的。因此,应该允许同时以信息和热力学度量对其进行定义。在这方面,布里渊公式 (公式9) 提供了一个强有力的工具,把信息和能量值置于同一个公式中,并且不加区分地处理它们。我们认为,将布里渊公式适当地应用于大脑处理环境,可以得到有趣的理论和实验结果。
5. 讨论
到目前为止,我们已经回顾了有关大脑活动的热力学模型的最新进展 (Prigogine,1978; La Cerra,2003; Varpula et al.,2013) ,并提出了 Friston 基于信息的模型。此外,我们还讨论并提出了从大脑活动和认知中获取信息的方法。然后,我们把信息论和热力学之间最重要的经典联系放在一起。此外,我们分析了大脑活动的热力学模型和Friston模型在概念上的细微差别,并通过信息和能量之间的经典联系将它们联系起来。我们重点讨论了来自Friston模型的自由能、惊奇和熵与热力学中等价概念间的理论关系。
信息和能量之间的关系已经在物理学、化学和生物学中得到了广泛的研究(Brilouin,1953; Prigogine,1978; Feynman et al.,1998; Del Castillo and Vera-Cruz,2011)。然而,这种联系并没有在神经科学领域形式化 (Del Castillo and Vera-Cruz,2011; Colell and Fauquet,2014) 。在这方面,本工作的主要贡献是从信息论和热力学之间的经典联系来解决大脑活动和认知的关联问题。在我们看来,理解大脑能量和认知信息间的权衡、边界和交换,将极大促进神经科学的发展。此外,我们认为,为解决哲学和科学问题,如意识的难题、大脑和心智的关系或自由意志的存在,必须将信息和能量连接大脑的方式适当形式化。此外,如上所述,该方法可以很方便地将大脑和认知活动中的自发性概念形式化。总之,我们的目标是激励更多的科学家从该框架中进一步研究大脑和认知之间的关系。也就是说构建新的数学模型,以连接现有的基于热力学和信息的模型,并设计实证检验。
参考文献
Anderson, J. R. (1996). ACT: a simple theory of complex cognition. Am. Psychol. 51, 355–365. doi: 10.1037/0003-066x.51.4.355
Anderson, J. R., and Fincham, J. M. (2014). Discovering the sequential structure of thought. Cogn. Sci. 38, 322–352. doi: 10.1111/cogs. 12068
Assecondi, S., Ostwald, D., and Bagshaw, A. P. (2015). Reliability of information-based Integration and fMRI data: a simulation study. Neural Comput. 27, 281–305. doi: 10.1162/NECO_a_00695
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Bennett, C. H. (1982). The thermodynamics of computation—a review. Int. J. Theor. Phys. 21, 905–940. doi: 10.1007/BF02084158
Boltzmann, L. (1877). Uber die beziehung dem zweiten Haubtsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht [On the relationship between the second main theorem of mechanical heat theory and the probability calculation with respect to the results about the heat equilibrium]. Wien. Ber. 76, 373–435.
Borst, A., and Theunissen, F. E. (1999). Information theory and neural coding. Nat. Neurosci. 2, 947–957. doi: 10.1038/14731
Brillouin, L. (1953). The negentropy principle of information. J. Appl. Phys. 24, 1152–1163. doi: 10.1063/1.1721463
Brunel, N., Hakim, V., Isope, P., Nadal, J. P., and Barbour, B. (2004). Optimal information storage and the distribution of synaptic weights: perceptron versus Purkinje cell. Neuron 43, 745–757. doi: 10.1016/j.neuron.2004.08.023
Collell, G., and Fauquet, J. (2014). “How the relationship between information theory and thermodynamics can contribute to explaining brain and cognitive activity: an integrative approach,” in Proceedings of the IEEE Sixth International Conference on Advanced Cognitive Technologies and Applications (COGNITIVE 2014) (Venice), 269–273.
De Castro, A. (2013). The thermodynamic cost of fast thought. Minds Mach. 23, 473–487. doi: 10.1007/s11023-013-9302-x
Del Castillo, L. F., and Vera-Cruz, P. (2011). Thermodynamic formulation of living systems and their evolution. J. Mod. Phys. 2, 379–391. doi: 10.4236/jmp.2011.25047
Feynman, R. P., Hey, J. G., and Allen, R. W. (1998). Feynman Lectures on Computation. Boston, MA: Addison-Wesley Longman Publishing Co. Feynman, R. P., Leighton, R. B., Sands, M., and Hafner, E. M. (1965). The feynman lectures on physics. Am. J. Phys. 33, 750–752. doi: 10.1119/1.1972241
Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138. doi: 10.1038/nrn2787
Friston, K. J., and Stephan, K. E. (2007). Free-energy and the brain. Synthese 159, 417–458. doi: 10.1007/s11229-007-9237-y
Fukushima, K. (1980). Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 36, 193–202. doi: 10.1007/BF00344251
Haimovici, A., Tagliazucchi, E., Balenzuela, P., and Chialvo, D. R. (2013). Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 110:178101. doi: 10.1103/PhysRevLett.110.178101
Hecht-Nielsen, R. (1989). “Theory of the backpropagation neural network,” in Neural Networks. International Joint Conference on Neural Networks(Washigton, DC), 593–605.
Howarth, C., Peppiatt-Wildman, C. M., and Attwell, D. (2010). The energy use associated with neural computation in the cerebellum. J. Cereb. Blood Flow Metab. 30, 403–414. doi: 10.1038/jcbfm.2009.231
Kirkaldy, J. S. (1965). Thermodynamics of the human brain. Biophys. J. 5, 981–986. doi: 10.1016/S0006-3495(65)86763-7
La Cerra, P. (2003). The first law of psychology is the second law of thermodynamics: the energetic evolutionary model of the mind and the generation of human psychological phenomena. Hum. Nat. Rev. 3, 440–447.
Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5, 183–191. doi: 10.1147/rd.53.0183
Laughlin, S. B., de Ruyter van Steveninck, R. R., and Anderson, J. C. (1998). The metabolic cost of neural information. Nat. Neurosci. 1, 36–41. doi: 10.1038/236
Lebon, G., Jou, D., and Casas-Vázquez, J. (2008). Understanding Non-Equilibrium Thermodynamics. Berlin: Springer-Verlag. Maruyama, K., Nori, F., and Vedral, V. (2009). Colloquium: the physics of Maxwell’s demon and information. Rev. Mod. Phys. 81, 1–23. doi: 10.1103/RevModPhys.81.1
Moran, R. J., Campo, P., Symmonds, M., Stephan, K. E., Dolan, R. J., and Friston, K. J. (2013). Free energy, precision and learning: the role of cholinergic neuromodulation. J. Neurosci. 33, 8227–8236. doi: 10.1523/JNEUROSCI.4255-12.2013
Narayanan, N. S., Kimchi, E. Y., and Laubach, M. (2005). Redundancy and synergy of neuronal ensembles in motor cortex. J. Neurosci. 25, 4207–4216. doi: 10.1523/JNEUROSCI.4697-04.2005
Plenio, M. B., and Vitelli, V. (2001). The physics of forgetting: landauer’s erasure principle and information theory. Contemp. Phys. 42, 25–60. doi: 10.1080/00107510010018916
Prigogine, I. (1978). Time, structure, and fluctuations. Science 201, 777–785. doi: 10.1126/science.201.4358.777
Ros, E., Carrillo, R., Ortigosa, E. M., Barbour, B., and Agís, R. (2006). Event-driven simulation scheme for spiking neural networks using lookup tables to characterize neuronal dynamics. Neural Comput. 18, 2959–2993. doi: 10.1162/neco.2006.18.12.2959
Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408. doi: 10.1037/h0042519
Rothstein, J. (1951). Information, measurement, and quantum mechanics. Science 114, 171–175. doi: 10.1126/science.114.2955.171
Schrodinger, E. (1944). What is Life? Cambridge: Cambridge University Press. Shannon, C. E. (1948). A mathematical theory of communication. Bell Labs Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Stephen, D. G., Dixon, J. A., and Isenhower, R. W. (2009). Dynamics of representational change: entropy, action, and cognition. J. Exp. Psychol. Hum. Percept. Perform. 35, 1811–1832. doi: 10.1037/a0014510
Szilard, L. (1929). On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Physik 53, 124–133.
Varpula, S., Annila, A., and Beck, C. (2013). Thoughts about thinking: cognition according to the second law of thermodynamics. Adv. Stud. Biol. 5, 135–149.
Vilar, J. M. G., and Rubí, J. M. (2001). Themodynamics “beyond” local equilibrium. Proc. Natl. Acad. Sci. U.S.A. 98, 11081–11084. doi: 10.1073/pnas.191360398
(参考文献可上下滑动查看)
原文链接:
https://www.frontiersin.org/articles/10.3389/fpsyg.2015.00818/full
未来智能实验室的主要工作包括:建立AI智能系统智商评测体系,开展世界人工智能智商评测;开展互联网(城市)大脑研究计划,构建互联网(城市)大脑技术和企业图谱,为提升企业,行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。
如果您对实验室的研究感兴趣,欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”

















,功能和目标)


