最短路径是在工程上经常用到的概念,在这里给出了从单源点到任意顶点的迪杰斯特拉算法。
先来看看基本概念:
用代码C语言实现如下:
#include<string.h>#include<ctype.h>#include<malloc.h> /* malloc()等 */#include<limits.h> /* INT_MAX等 */#include<stdio.h> /* EOF(=^Z或F6),NULL */#include<stdlib.h> /* atoi() */#include<io.h> /* eof() */#include<math.h> /* floor(),ceil(),abs() */#include<process.h> /* exit() *//* 函数结果状态代码 */#define TRUE 1#define FALSE 0#define OK 1#define ERROR 0#define INFEASIBLE -1typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */#define MAX_NAME 5 /* 顶点字符串的最大长度 */typedef int InfoType;typedef char VertexType[MAX_NAME]; /* 字符串类型 *//* c7-2.h 图的邻接表存储表示 */#define MAX_VERTEX_NUM 20typedef enum{DG,DN,AG,AN}GraphKind; /* {有向图,有向网,无向图,无向网} */typedef struct ArcNode{int adjvex; /* 该弧所指向的顶点的位置 */struct ArcNode *nextarc; /* 指向下一条弧的指针 */InfoType *info; /* 网的权值指针) */}ArcNode; /* 表结点 */typedef struct{VertexType data; /* 顶点信息 */ArcNode *firstarc; /* 第一个表结点的地址,指向第一条依附该顶点的弧的指针 */}VNode,AdjList[MAX_VERTEX_NUM]; /* 头结点 */typedef struct{AdjList vertices;int vexnum,arcnum; /* 图的当前顶点数和弧数 */int kind; /* 图的种类标志 */}ALGraph;
typedef int VRType;typedef char InfoType;typedef char VertexType[MAX_NAME];
typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef int ShortPathTable[MAX_VERTEX_NUM];void ShortestPath_DIJ(MGraph G,int v0,PathMatrix *P,ShortPathTable *D){ /* 用Dijkstra算法求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度 *//* D[v]。若P[v][w]为TRUE,则w是从v0到v当前求得最短路径上的顶点。 *//* final[v]为TRUE当且仅当v∈S,即已经求得从v0到v的最短路径 算法7.15 */int v,w,i,j,min;Status final[MAX_VERTEX_NUM];for(v=0;v<G.vexnum;++v){final[v]=FALSE;(*D)[v]=G.arcs[v0][v].adj;for(w=0;w<G.vexnum;++w)(*P)[v][w]=FALSE; /* 设空路径 */if((*D)[v]<INFINITY){(*P)[v][v0]=TRUE;(*P)[v][v]=TRUE;}}(*D)[v0]=0;final[v0]=TRUE; /* 初始化,v0顶点属于S集 */for(i=1;i<G.vexnum;++i) /* 其余G.vexnum-1个顶点 */{ /* 开始主循环,每次求得v0到某个v顶点的最短路径,并加v到S集 */min=INFINITY; /* 当前所知离v0顶点的最近距离 */for(w=0;w<G.vexnum;++w)if(!final[w]) /* w顶点在V-S中 */if((*D)[w]<min){v=w;min=(*D)[w];} /* w顶点离v0顶点更近 */final[v]=TRUE; /* 离v0顶点最近的v加入S集 */for(w=0;w<G.vexnum;++w) /* 更新当前最短路径及距离 */{if(!final[w]&&min<INFINITY&&G.arcs[v][w].adj<INFINITY&&(min+G.arcs[v][w].adj<(*D)[w])){ /* 修改D[w]和P[w],w∈V-S */(*D)[w]=min+G.arcs[v][w].adj;for(j=0;j<G.vexnum;++j)(*P)[w][j]=(*P)[v][j];(*P)[w][w]=TRUE;}}}}void main(){int i,j,v0=0; /* v0为源点 */MGraph g;PathMatrix p;ShortPathTable d;CreateDN(&g);ShortestPath_DIJ(g,v0,&p,&d);printf("最短路径数组p[i][j]如下:\n");for(i=0;i<g.vexnum;++i){for(j=0;j<g.vexnum;++j)printf("%2d",p[i][j]);printf("\n");}printf("%s到各顶点的最短路径长度为:\n",g.vexs[0]);for(i=1;i<g.vexnum;++i)printf("%s-%s:%d\n",g.vexs[0],g.vexs[i],d[i]);}
算法时间复杂度:O(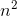










方法为什么返回值是int)















